Exponenta Banner

mdwtcluster

Мультисигнализирует о 1D кластеризации

Синтаксис

S = mdwtcluster(X)
S = mdwtcluster(X,'PropName1',PropVal1,'PropName2',PropVal2,...)

Описание

S = mdwtcluster(X) кластеры построений от иерархического кластерного дерева. Входная матрица X анализируется в направлении строки с помощью функции DWT с haar вейвлет и максимальный допустимый уровень.

S = mdwtcluster(X,'PropName1',PropVal1,'PropName2',PropVal2,...) позволяет вам изменять некоторые свойства. Допустимый выбор для PropName :

Примечание

mdwtcluster требует Statistics and Machine Learning Toolbox™

'dirDec'

'r' (строка) или 'c' (столбец). Значением по умолчанию является 'r'.

'level'

Уровень разложения DWT. Значение по умолчанию:
level=fix(log2(size(X,d)))
где d=1 или d=2, В зависимости от dirDec значение.

'wname'

Имя вейвлета используется в DWT. Значением по умолчанию является 'haar'.

'dwtEXTM'

Режим расширения DWT (см. dwtmode).

'pdist'

См. Statistics and Machine Learning Toolbox pdist функция. Значением по умолчанию является 'euclidean'.

'linkage'

См. Statistics and Machine Learning Toolbox linkage функция. Значением по умолчанию является 'ward'.

'maxclust'

Количество кластеров. Значение по умолчанию равняется 6. Входная переменная может быть вектором.

'lst2clu'

Массив ячеек, который содержит список данных, чтобы классифицировать.

Если N уровень разложения, позволенные значения имени для ячеек:

  • 's' — Сигнал

  • 'aj' — Приближение на уровне j

  • 'dj' — Детализируйте на уровне j

  • 'caj' — Коэффициенты приближения на уровне j

  • 'cdj' — Коэффициенты детали на уровне j

Значением по умолчанию является {'s';'ca1';...;'caN'}.

Структура output S такова это для каждого раздела j:

S.Idx(:,j)

Содержит кластерные числа, полученные из иерархического кластерного дерева (см. cluster в программном обеспечении Statistics and Machine Learning Toolbox).

S.Incons(:,j)

Содержит противоречивые значения каждого узла, не являющегося листом в иерархическом кластерном дереве (см., что программное обеспечение Statistics and Machine Learning Toolbox функционирует inconsistent).

S.Corr(j)

Содержит cophenetic коэффициенты корреляции раздела (см., что программное обеспечение Statistics and Machine Learning Toolbox функционирует cophenet).

Примечание

Если maxclustVal вектор, затем IdxCLU многомерный массив, таким образом что IdxCLU(:,j,k) содержит кластерные числа, полученные из иерархического кластерного дерева для k кластеры.

Примеры

load elecsig10
lst2clu = {'s','ca1','ca3','ca6'};

% Compute the structure resulting from multisignal clustering
S = mdwtcluster(signals,'maxclust',4,'lst2clu',lst2clu)

S = 

    IdxCLU: [70x4 double]
    Incons: [69x4 double]
      Corr: [0.7920 0.7926 0.7947 0.7631]

% Retrieve indices of clusters
IdxCLU = S.IdxCLU;

% Plot the first cluster
plot(signals(IdxCLU(:,1)==1,:)','r');
hold on; 

% Plot the third clustering
plot(signals(IdxCLU(:,1)==3,:)','b')



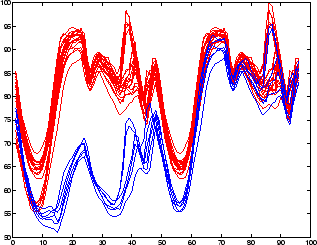
% Check the equality of partitions
equalPART = isequal(IdxCLU(:,1),IdxCLU(:,3))

equalPART =

     1

% So we can see that we obtain the same partitions using
% coefficents of approximation at level 3 instead of original
% signals. Much less information is then used.

Смотрите также

|

Введенный в R2008a

Документация Wavelet Toolbox
Поддержка