Критически выбранные и сверхдискретизированные наборы фильтров вейвлета

Наборы фильтров вейвлета являются особыми случаями названных наборов фильтров банков многоскоростного фильтра с древовидной структурой. В наборе фильтров два или больше фильтра применяются к входному сигналу и фильтру, выходные параметры обычно прореживаются. Следующая фигура иллюстрирует два этапа или уровни, критически произведенного двухканального аналитического набора фильтров с древовидной структурой. Фильтры изображены в области z.

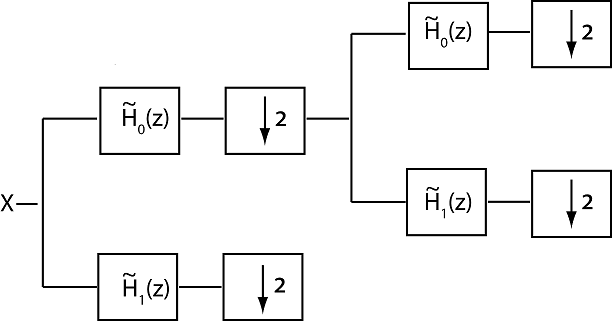
Системные функции фильтра, ${\tilde{H}}_{0} (z)$ и ${\tilde{H}}_{1} (z)$ , обычно проектируются к, приблизительно делят входной сигнал, X, в непересекающиеся поддиапазоны. В вейвлете наборы фильтров с древовидной структурой, фильтр ${\tilde{H}}_{0} (z)$ lowpass, или масштабирование, фильтр, с ненулевой частотной характеристикой на интервале [-π/2, π/2] радианы/выборка или [-1/4, 1/4] циклы/выборка. Фильтр ${\tilde{H}}_{1} (z)$ highpass, или вейвлет, фильтр, с ненулевой частотной характеристикой на интервале [-π,-π/2] ∪ [π/2, π] радианы/выборка или [-1/2,-1/4] ∪ [1/4, 1/2] циклы/выборка. Набор фильтров выполняет итерации на выходе аналитического фильтра lowpass, чтобы получить последовательные уровни, заканчивающиеся в аппроксимированную фильтрацию полосы октавы входа. Два аналитических фильтра не идеальны, который приводит к искажению, которое должно быть отменено соответственно спроектированными фильтрами синтеза для совершенной реконструкции. Для ортогонального набора фильтров объединение масштабирующегося фильтра и даже сдвиги и фильтр вейвлета и даже сдвиги формирует ортонормированный базис для пробела квадратно-суммируемых последовательностей, $ℓ^{2} (ℤ)$ . Фильтры синтеза являются реверсом времени, и спрягается аналитических фильтров. Для биоортогональных наборов фильтров фильтров синтеза и их даже сдвиги формируют обратную величину, или двойной, основание к аналитическим фильтрам. С двумя аналитическими фильтрами, прореживая выход каждого аналитического фильтра по два на каждом этапе гарантирует, что общее количество выходных выборок равняется количеству входных выборок. Случай, где количество аналитических фильтров равно фактору субдискретизации, упоминается как критическая выборка. Аналитический набор фильтров, где количество каналов больше фактора субдискретизации, является сверхдискретизированным набором фильтров.

Вейвлет с удвоенной плотностью преобразовывает

Следующая фигура иллюстрирует два уровня сверхдискретизированного аналитического набора фильтров с тремя каналами и фактором субдискретизации два. Фильтры изображены в области z.

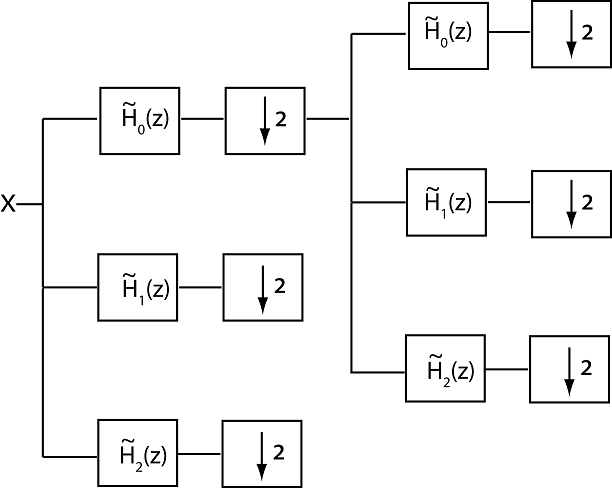
Примите фильтр ${\tilde{H}}_{0} (z)$ , полуленточный фильтр lowpass и фильтры ${\tilde{H}}_{1} (z)$ и ${\tilde{H}}_{2} (z)$ highpass полуленточные фильтры.

Примите, что три фильтра вместе с соответствующими фильтрами синтеза формируют совершенный набор фильтров реконструкции. Если дополнительно, ${\tilde{H}}_{1} (z)$ и ${\tilde{H}}_{2} (z)$ сгенерируйте вейвлеты, которые удовлетворяют следующему отношению

$ψ_{1} (t) = ψ_{2} (t - 1 / 2),$

реализации набора фильтров вейвлет с удвоенной плотностью преобразовывают. Предыдущее условие гарантирует, что целое число переводит одного падения вейвлета на полпути между целым числом, переводит второго вейвлета. В теоретических системой координат терминах вейвлет с удвоенной плотностью преобразовывает, реализует трудное расширение системы координат.

Следующий код иллюстрирует, что эти два вейвлета, используемые в вейвлете с удвоенной плотностью, преобразовывают.

x = zeros(256,1);
df = dtfilters('filters1');
wt1 = dddtree('ddt',x,5,df,df);
wt2 = dddtree('ddt',x,5,df,df);
wt1.cfs{5}(5,1,1) = 1;
wt2.cfs{5}(5,1,2) = 1;
wav1 = idddtree(wt1);
wav2 = idddtree(wt2);
plot(wav1); hold on;
plot(wav2,'r'); axis tight;
legend('\psi_1(t)','\psi_2(t)')

Вы не можете выбрать, два фильтра вейвлета произвольно, чтобы реализовать вейвлет с удвоенной плотностью преобразовывают. Три фильтра анализа и синтеза должны удовлетворить условиям совершенной реконструкции (PR). Для трех фильтров с действительным знаком условия PR

$\begin{array}{l} H_{0} (z) H_{0} (1 / z) + H_{1} (z) H_{1} (1 / z) + H_{2} (z) H_{2} (1 / z) = 2 \\ H_{0} (z) H_{0} (- 1 / z) + H_{1} (z) H_{1} (- 1 / z) + H_{2} (z) H_{2} (- 1 / z) = 0 \end{array}$

Можно получить системы координат анализа и синтеза вейвлета для вейвлета с удвоенной плотностью, преобразовывают с 6 и 12 касаниями с помощью dtfilters.

[df1,sf1] = dtfilters('filters1');
[df2,sf2] = dtfilters('filters2');

df1 и df2 матрицы с тремя столбцами, содержащие аналитические фильтры. Первый столбец содержит масштабирующийся фильтр, и столбцы два и три содержат фильтры вейвлета. Соответствующие фильтры синтеза находятся в sf1 и sf2.

См. [4] и [5] для получения дополнительной информации о том, как сгенерировать системы координат вейвлета для вейвлета с удвоенной плотностью, преобразовывают.

Основные преимущества вейвлета с удвоенной плотностью преобразовывают по критически произведенному дискретному вейвлету, преобразовывают,

Уменьшаемая чувствительность сдвига
Уменьшаемые прямоугольные артефакты в 2D преобразовании
Более сглаженные вейвлеты для данного номера исчезающих моментов

Основные недостатки

Увеличенные вычислительные затраты
Неортогональное преобразование

Кроме того, при показе меньшей чувствительности сдвига, чем критически произведенный DWT, DWT с удвоенной плотностью не является shift-invariant как комплексный двойной древовидный вейвлет, преобразовывают. Вейвлет с удвоенной плотностью преобразовывает, также недостает, направленная селективность ориентированного двойного древовидного вейвлета преобразовывает.

Двойной древовидный комплексный вейвлет преобразовывает

Критически произведенный дискретный вейвлет преобразовывает (DWT) страдает от отсутствия инвариантности сдвига в 1D и направленной чувствительности в N-D. Можно смягчить эти недостатки приблизительно при помощи аналитических вейвлетов. Аналитический вейвлет задан как

$ψ_{c} (t) = ψ_{r} (t) + j ψ_{i} (t)$

где j обозначает мнимый модуль. Мнимая часть вейвлета, _ψi(t), является преобразованием Гильберта действительной части, _ψr(t). В частотном диапазоне аналитический вейвлет имеет поддержку только на одной половине оси частоты. Это означает, что аналитический вейвлет _ψc(t) имеет только одну половину пропускной способности вейвлета с действительным знаком _ψr(t).

Не возможно получить точно аналитические вейвлеты, сгенерированные КИХ-фильтрами. Преобразования Фурье сжато поддерживаемых вейвлетов не могут исчезнуть ни на каком наборе ненулевой меры. Это означает, что преобразование Фурье не может быть нулем на отрицательной оси частоты. Кроме того, эффективная двухканальная реализация набора фильтров DWT выводит из следующего совершенного условия реконструкции для масштабирующегося фильтра, $H_{0} (e^{j ω})$ , из анализа мультиразрешения (MRA)

$| H_{0} (e^{j ω}) |^{2} + | H_{0} (e^{j (ω + π)}) |^{2} = 2.$

Если вейвлет, сопоставленный с MRA, аналитичен, масштабирующаяся функция также аналитична. Это подразумевает это

$H_{0} (e^{j ω}) = 0 - π \leq ω < 0,$

от который из этого следует, что $| H_{0} (e^{j ω}) |^{2} = 2 0 \leq ω \leq π .$ Результат состоит в том, что масштабирующийся фильтр является allpass.

Предыдущие результаты демонстрируют, что вы не можете найти сжато вейвлет поддержки определенный КИХ-фильтрами, который точно аналитичен. Однако можно получить вейвлеты, которые приблизительно аналитичны путем объединения двух наборов фильтров с древовидной структурой, пока фильтры в двойном древовидном преобразовании тщательно создаются, чтобы удовлетворить определенным обстоятельствам [1], [6].

Двойной древовидный комплексный вейвлет преобразовывает, реализован с двумя отдельными двухканальными КИХ-наборами фильтров. Выход одного набора фильтров считается действительной частью, в то время как выход другого набора фильтров является мнимой частью. Поскольку двойной древовидный комплексный вейвлет преобразовывает использование два критически произведенных набора фильтров, сокращение является ^2-м для сигнала d-dimensional (изображение). Существует несколько критических факторов в реализации двойного древовидного комплексного вейвлета, преобразовывают. Для удобства обратитесь к этим двум деревьям как: Дерево A и Дерево B.

Анализ просачивается, первая стадия каждого набора фильтров должна отличаться от фильтров, используемых на последующих этапах в обоих деревьях. Это не важно, который масштабирование и вейвлет фильтрует вас использование в этих двух деревьях для этапа 1. Можно использовать то же масштабирование первой стадии, и вейвлет просачивается оба дерева.
Масштабирование просачивается, Дерево B для этапов ≥ 2 должно аппроксимировать 1/2 демонстрационную задержку масштабирования, просачиваются Дерево A. Половина демонстрационного условия задержки является необходимым и достаточным условием для соответствующего Дерева B вейвлет, чтобы быть преобразованием Гильберта Дерева вейвлет. [3].

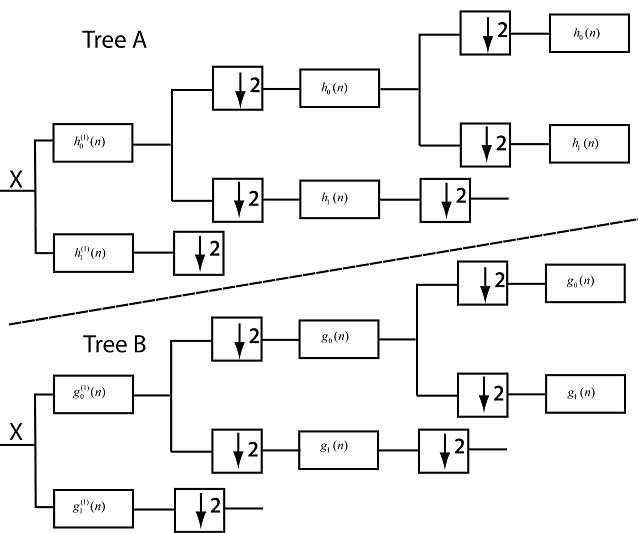
Следующая фигура иллюстрирует, что три этапа аналитического набора фильтров для 1D двойного древовидного комплексного вейвлета преобразовывают. КИХ-фильтры масштабирования для этих двух деревьев обозначаются ${h_{0} (n), g_{0} (n)}$ . КИХ-фильтры вейвлета для этих двух деревьев обозначаются ${h_{1} (n), g_{1} (n)}$ . Два масштабирующихся фильтра спроектированы, чтобы приблизительно удовлетворить полудемонстрационному условию задержки

$g_{0} (n) = h_{0} (n - 1 / 2)$

Верхний индекс (1) обозначает, что фильтры первой стадии должны отличаться от фильтров, используемых на последующих этапах. Можно использовать любую допустимую пару фильтра вейвлета масштабирования в первой стадии. Фильтры ${h_{0} (n), g_{0} (n)}$ не может быть произвольные фильтры масштабирования и предоставить преимущества использования приблизительно аналитических вейвлетов.

2D двойной древовидный вейвлет преобразовывает

Двойной древовидный вейвлет преобразовывает приблизительно с существенными преимуществами предложений аналитических вейвлетов перед отделимым 2D DWT для обработки изображений. Традиционный отделимый 2D DWT страдает от артефактов шахматной доски из-за симметричной поддержки частоты (неаналитических) функций масштабирования с действительным знаком и вейвлетов. Кроме того, критически произведенный отделимый 2D DWT испытывает недостаток в инвариантности сдвига так же, как 1D критически произвело DWT, делает. Поддержки программного обеспечения Wavelet Toolbox™, которые два варианта двойного древовидного 2D вейвлета преобразовывают, действительный ориентированный двойной древовидный вейвлет, преобразовывают, и ориентированный 2D двойной древовидный комплексный вейвлет преобразовывают. Оба описаны подробно в [6].

Действительное ориентированное двойное древовидное преобразование состоит из двух отделимых (фильтрация строки и столбца) наборы фильтров вейвлета, действующие параллельно. Комплекс ориентировался, 2D вейвлет преобразовывают, требует четырех отделимых наборов фильтров вейвлета и поэтому не технически двойное древовидное преобразование. Однако это упоминается как двойное древовидное преобразование, потому что это - естественное расширение 1D комплексного двойного дерева, преобразовывают. Чтобы реализовать действительный ориентированный двойной древовидный вейвлет преобразовывают, используют 'realdt' опция в dddtree2. Чтобы реализовать ориентированное комплексное двойное дерево преобразовывают, используют 'cplxdt' опция.

Оба, которых преобразовывает действительное ориентированное и ориентированное комплексное двойное дерево, чувствительны к направленным функциям в изображении. Только ориентированное комплексное двойное дерево преобразовывает, приблизительно инвариант сдвига. Инвариантность сдвига не является функцией, находившейся в собственности действительным ориентированным двойным древовидным преобразованием.

Двойной древовидный вейвлет с удвоенной плотностью преобразовывает

Двойной древовидный вейвлет с удвоенной плотностью преобразовывает, комбинирует свойства вейвлета с удвоенной плотностью, преобразовывают, и двойной древовидный вейвлет преобразовывают [2].

В 1D двойной древовидный вейвлет с удвоенной плотностью преобразовывает, состоит из двух наборов фильтров с тремя каналами. Эти два вейвлета в каждом дереве удовлетворяют условиям, описанным в Преобразовании Вейвлета С удвоенной плотностью. А именно, целое число переводит одного падения вейвлета на полпути между целым числом, переводит второго вейвлета. Кроме того, вейвлеты в Дереве B являются аппроксимированным преобразованием Гильберта вейвлетов в Дереве A. Чтобы реализовать двойной древовидный вейвлет с удвоенной плотностью преобразовывают для 1D сигналов, используют 'cplxdddt' опция в dddtree. Подобно двойному древовидному вейвлету преобразовывают, двойной древовидный вейвлет с удвоенной плотностью преобразовывают, обеспечивает и действительный ориентированный и комплексный ориентированный вейвлет, преобразовывает в 2D. Чтобы получить действительный ориентированный двойной древовидный вейвлет с удвоенной плотностью преобразовывают, используют 'realdddt' опция в dddtree2. Получить комплекс ориентировалось, двойной древовидный вейвлет с удвоенной плотностью преобразовывают, используют 'cplxdddt' опция.

Ссылки

[1] Кингсбери, N.G. “Комплексные Вейвлеты для Анализа Инварианта Сдвига и Фильтрации Сигналов”. Журнал Прикладного и Вычислительного Гармонического Анализа. Vol 10, Номер 3, май 2001, стр 234-253.

[2] Selesnick, я. “Двойное Древовидное Преобразование Вейвлета С удвоенной плотностью”. IEEE^® Transactions на Обработке сигналов. Издание 52, Номер 5, май 2004, стр 1304–1314.

[3] Selesnick, я. “Проект Аппроксимированных Пар преобразования Гильберта Основ Вейвлета”. Транзакции IEEE на Обработке сигналов, Издании 50, Номере 5, стр 1144–1152.

[4] Selesnick, я. “Двойная плотность DWT” Вейвлеты в и Анализе изображения Сигнала: От Теории до Практики (A.A Petrosian, Ф.Г. Мейер, редакторы). Norwell, MA: Kluwer Академические Издатели: 2001.

[5] Abdelnour, F. “Симметричные Вейвлеты Двухместные Одноуровневые элементы и Двойные Системы координат” Обработка сигналов, Издание 92, Номер 5, 2012, стр 1216–1225.

[6] Selesnick, я. R.G Baraniuk и Н.Г. Кингсбери. “Двойное Древовидное Комплексное Преобразование Вейвлета”. Журнал Обработки сигналов IEEE. Издание 22, Номер 6, ноябрь 2005, стр 123–151.

[7] Vetterli, M. “Вейвлеты, Приближение и Сжатие”. Журнал Обработки сигналов IEEE, Издание 18, Номер 5, сентябрь 2001, стр 59–73.

Документация