Системы Shearlet

shearlet система позволяет вам создать направлено чувствительные разреженные представления изображений с анизотропными функциями. Shearlets используются в приложениях для обработки изображений включая шумоподавление, сжатие, восстановление и извлечение признаков. Shearlets также используются в статистическом обучении решить проблемы классификации изображений, обратные проблемы рассеивания, такие как томография и разделение данных. Можно найти дополнительное применение в ShearLab [5].

Сила анализа вейвлета для 1D сигналов является своей способностью эффективно представлять сглаженные функции, которые имеют pointwise разрывы. Однако вейвлеты не представляют изогнутую сингулярность, такую как ребро диска в изображении, так редко, как они делают pointwise разрывы. Геометрический многошкальный анализ является попыткой спроектировать системы, способные к эффективному представлению кривой сингулярности в более высоких размерных данных. В дополнение к shearlets другие геометрические многошкальные системы включают curvelets, contourlets, и ободки.

Го, Kutyniok и Labate [1] вели разработку теории shearlets. Они. также разработанные эффективные алгоритмы для shearlet преобразовывают [4], как имеют Häuser и Steidl [6]. ShearLab [5] обеспечивает обширный набор алгоритмов для обработки 2D и 3D данных с помощью shearlets.

Как вейвлеты, имеет отношение всесторонняя теория, непрерывные shearlet преобразовывают с дискретным преобразованием. Кроме того, аналитическая среда мультиразрешения существует для shearlets. Как следует из названия, shearlets имеют достойную внимания особенность использования сдвигов, не вращений, чтобы управлять направленной чувствительностью. Эта характеристика позволяет вам создавать shearlet систему из одного или конечного множества производящих функций. Другие причины успеха shearlets включают:

Shearlets обеспечивают оптимально разреженные приближения анизотропных функций многомерных данных.
И сжато поддерживаемый и bandlimited shearlets существуют.
Shearlet преобразовывает, имеют эффективные алгоритмические реализации.

Shearlets

Подобно вейвлетам shearlets не имеют уникальной системы. Расширение, сдвиг и операции перевода генерируют shearlets. Расширение может быть выражено как матрица, $A_{a} = (\begin{matrix} a^{1 / 2} & 0 \\ 0 & a^{- 1 / 2} \end{matrix})$ где $a \in ℝ^{+} .$ Сдвиг может быть выражен как $S_{s} = (\begin{matrix} 1 & s \\ 0 & 1 \end{matrix})$ где $s \in ℝ .$ Переменная s параметрирует ориентации.

Если функция $ψ \in L^{2} (ℝ^{2})$ удовлетворяет бесспорный (допустимость) условия, затем набор функций

$S H {ψ} = {ψ_{a, s, t} = a^{3 / 4} ψ (S_{s} A_{a} (\cdot - t))}$

непрерывная shearlet система, где a и s заданы, как отмечено ранее, и $t \in ℝ^{2} .$

Если вы дискретизируете расширение, сдвиг и параметры перевода соответственно, вы получаете дискретную shearlet систему:

$S H (ψ) = {ψ_{j, k, m} = 2^{\frac{3}{4} j} ψ (S_{k} A_{2^{j}} \cdot - m) : j, k \in ℤ, m \in ℤ^{2}} .$

Функциональный shearletSystem создает адаптированный к конусу bandlimited shearlet система. Реализация shearletSystem функция следует за подходом, описанным в Häuser и Steidl [6]. shearlet система является примером системы координат, которую можно нормировать, чтобы создать систему координат Parseval. Дискретное shearlet преобразование функции $f \in L^{2} (ℝ^{2})$ скалярное произведение $f$ со всем shearlets в дискретной shearlet системе $〈 f, ψ_{j, k, m} 〉$ где $(j, k, m) \in ℤ \times ℤ \times ℤ^{2} .$ Вы используете sheart2 взять дискретное shearlet преобразование изображения. Для получения дополнительной информации смотрите Ссылки.

Следующий рисунок показывает, как адаптированная к конусу shearlet система делит 2D плоскость частоты. Изображение слева показывает раздел адаптированной к конусу shearlet системы с действительным знаком с одной шкалой. Область R в центре является частью lowpass системы. Кроме того, изображение включает горизонтальный конус shearlet (симметричный в частоте, потому что это действительно оцененный), и вертикальный конус shearlet. Изображение справа изображает систему с тремя шкалами. Подобный вентилятору шаблон дает shearlet системе свою направленную чувствительность. Обратите внимание на то, что количество сдвига факторов увеличивается как поддержка частоты увеличений shearlet. Когда поддержка в частотном диапазоне увеличивается, поддержка в пространственных доменных уменьшениях.

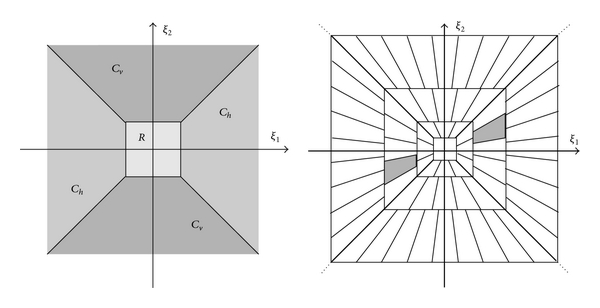
Спектры shearlets с действительным знаком являются тем же самым по положительному и отрицательному _ξ1, _ξ2 поддержки. Shearlets в shearlet системном разделе с комплексным знаком индивидуально, не в парах.

Преобразуйте тип

Shearlets или действительны оцененный или объединяют оцененный в пространственной области. Вы задаете тип преобразования, когда вы используете shearletSystem создать систему. shearlets с действительным знаком имеют двухсторонние спектры частоты. Преобразования Фурье shearlets с комплексным знаком имеют поддержку только на одной половине 2D пространства частоты. Преобразования Фурье обоих типов shearlets действительны оцененный.

Ссылки

[1] Го, K., Г. Кутинайок и Д. Лэбэйт. "Разреженные многомерные представления с помощью анизотропного расширения и операторов сдвига". Вейвлеты и Сплайны: Афины 2005 (Г. Чен и M.-J. Чен, редакторы), 189–201. Брентвуд, TN: Нажатие Nashboro, 2006.

[2] Го, K. и Д. Лэбэйт. "Оптимально Разреженное Многомерное Представление Используя Shearlets". SIAM Journal на Математическом анализе. Издание 39, Номер 1, 2007, стр 298–318.

[3] Kutyniok, G. и Лим W.-Q. "Сжато поддерживаемые shearlets оптимально разреженны". Журнал Теории Приближения. Издание 163, Номер 11, 2011, стр 1564–1589.

[4] Shearlets: Многошкальный Анализ для Многомерных Данных (Г. Кутинайок, и Д. Лэбэйт, редакторы). Нью-Йорк: Спрингер, 2012.

[5] ShearLab. https://www3.math.tu-berlin.de/numerik/www.shearlab.org/.

[6] Häuser, S. и Г. Стейдл. "Быстро Конечное Преобразование Shearlet: пример". arXiv предварительно распечатывают arXiv:1202.1773 (2014).

[7] Rezaeilouyeh, H., А. Моллаоссейни и М. Мэхур. "Микроскопическая медицинская среда классификации изображений через глубокое обучение и shearlet преобразовывает". Журнал Медицинской Обработки изображений. Издание 3, Номер 4, 044501, 2016. doi:10.1117/1. JMI.3.4.044501.

Документация