Гибридный метод MoM-PO для металлических антенн с большими рассеивателями

Гибридная физическая оптика (PO) метода моментов (MoM) вычислительный метод в Antenna Toolbox™ позволяет вам антеннам модели около больших рассеивателей, таких как параболические отражатели. Антенный элемент моделируется с помощью MoM, в то время как эффектом электрически больших структур является рассмотренная использование ПО.

Субдомен основные функции RWG и дополнительные размерности

Знакомые основные функции Вильтона Рао Глиссона (RWG) на треугольниках основаны [2].

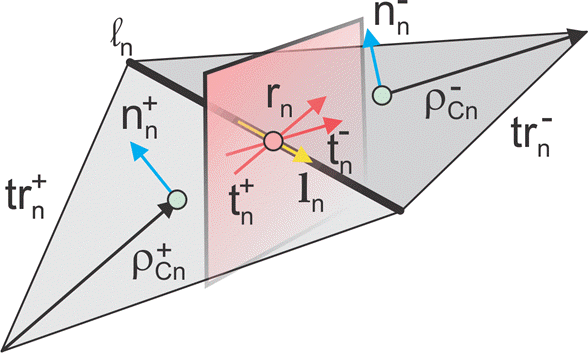
В изображении для двух произвольных треугольных закрашенных фигур _trn+ и _trn-, имеющий области _An+ и _An- и совместно использующий общее ребро_{, ln} основные функции имеет форму

${\vec{f}}_{n} (\vec{r}) = {\begin{cases} \frac{l_{n}}{2 A_{n}^{+}} {\vec{ρ}}_{n}^{+} \vec{r} \in t r_{n}^{+} \\ \frac{l_{n}}{2 A_{n}^{-}} {\vec{ρ}}_{n}^{-} \vec{r} \in t r_{n}^{-} \end{cases}} (1)$

где ${\vec{ρ}}_{n}^{+} = \vec{r} - {\vec{r}}_{n}^{-}$ вектор, чертивший от свободной вершины треугольного _trn+ к наблюдательному посту $\vec{r}$ ; ${\vec{ρ}}_{n}^{-} = {\vec{r}}_{n}^{-} - \vec{r}$ вектор, чертивший от наблюдательного поста до свободной вершины треугольного _trn-. Основная функция является нулем вне двух смежных треугольников. Векторная основная функция RWG линейна и не имеет никакого потока (то есть, не имеет никакого нормального компонента) через его контур.

От [1], наряду со стандартным определением, этот метод требует двух модульных векторов нормали ${\vec{n}}_{n}^{\pm}$ и 2D единичные векторы ${\vec{t}}_{n}^{\pm}$ также показанный на рисунке. Вектор ${\vec{t}}_{n}^{+}$ плоскость треугольного _trn+; оба вектора перпендикулярны ребру _ln. Они заданы в центре ребра, который is_ln, обозначенный ${\vec{r}}_{n}$ . Направления ${\vec{t}}_{n}^{\pm}$

также показаны на рисунке. Этот метод принимает, что векторы нормали правильно (угол между смежным ${\vec{n}}_{n}^{\pm}$ должен быть меньше 180 градусов), и исключительно заданный. Определенная векторная ориентация (e.g. внешние или внутренние векторы нормали), не имеет значения. Мы затем формируем два вектора векторного произведения ${\vec{l}}_{n}^{\pm}$ ,

${\vec{l}}_{n}^{\pm} = {\vec{t}}_{n}^{\pm} \times {\vec{n}}_{n}^{\pm} (2)$

и установите, что оба таких единичных вектора, направленные вдоль ребра, идентичны,

${\vec{l}}_{n}^{\pm} = {\vec{l}}_{n}^{-} = {\vec{l}}_{n} (3)$

Только вектор ${\vec{l}}_{n}$ в конечном счете необходим.

Область MoM и область ФО

Поверхностная плотность тока, $\vec{J} (\vec{r})$ , на целой металлической поверхности расширен в N основные функции RWG. Однако часть таких основных функций принадлежит области MoM (или "точная область"), в то время как другая часть будет принадлежать Области ФО (или "аппроксимируют область"). Эти основные функции (или области) могут перекрыться и быть произвольно распределены на пробеле (не обязательно быть непрерывными). Метод принимает что основные функции _NMoM из области MoM впереди в списке и основных функциях _NPO для Области ФО позже. Поэтому вы имеете $(N_{P O} + N_{M o M} = N)$

$\vec{J} (\vec{r}) = \sum_{n = 1}^{N_{M o M}} I_{n}^{M o M} {\vec{f}}_{n} (\vec{r}), \vec{J} (\vec{r}) = \sum_{n = 1}^{N_{P O}} I_{n}^{P O} {\vec{f}}_{n + N_{M o M}} (\vec{r}) (4)$

Решение MoM и решение ФО

Если нет никакой Области ФО, можно решить целую задачу с помощью MoM с одним квадратом системная матрица MoM $\hat{Z}$ , который может быть подразделен на 4 матрицы как показано.

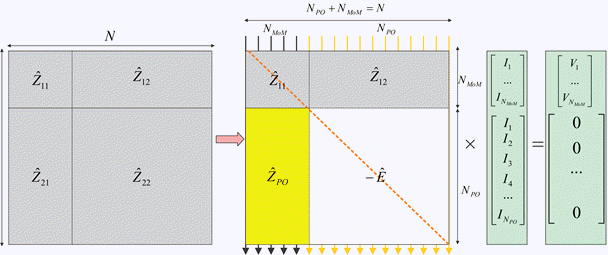
$\hat{Z} = (\begin{matrix} {\hat{Z}}_{11} & {\hat{Z}}_{12} \\ {\hat{Z}}_{21} & {\hat{Z}}_{22} \end{matrix}), \dim ({\hat{Z}}_{11}) = N_{M o M} \times N_{M o M}, \dim ({\hat{Z}}_{12}) = N_{M o M} \times N_{P O} (5)$

Рисунок показывает матричную интерпретацию гибридного MoM-PO и его сравнения с плоскостью решение MoM. Метод принимает, что подача антенны дает вектор, $\vec{V}$ это описывает возбуждение, которое принадлежит области MoM только.

Гибридное решение сохраняет подматрицы ${\hat{Z}}_{11}$ и ${\hat{Z}}_{12}$ . Другими словами, метод решает стандартную систему линейных уравнений для области MoM где излучение от Области ФО через ${\hat{Z}}_{12}$ рассматривается.

Гибридное решение игнорирует подматрицы, ${\hat{Z}}_{22}$ полностью. Здесь, токи в Области ФО не взаимодействуют друг с другом. Они найдены через излученное магнитное поле, $\vec{H} (\vec{r})$ , из области MoM, с помощью Приближения ФО [1]. Новая матрица описывает эту операцию, ${\hat{Z}}_{P O}$ , и отрицательная единичная матрица, E, который заменяет ${\hat{Z}}_{22}$ .

Открытие _ZPO

Подходящее Приближение ФО имеет форму [1]

$\vec{J} (\vec{r}) = 2 δ (\vec{r}) [\vec{n} (\vec{r}) \times \vec{H} (\vec{r})] (6)$

где δ составляет теневые эффекты. Если наблюдательный пост находится в теневой области, δ должен быть нулем. В противном случае это равняется ±1 в зависимости от направления падения относительно вектора нормали ориентации $\vec{n} (\vec{r})$ . Используя второй Eq. (4) выражения:

$\sum_{n = 1}^{N_{P O}} I_{n}^{P O} {\vec{f}}_{n + N_{M o M}} (\vec{r}) = 2 δ (\vec{r}) [\vec{n} (\vec{r}) \times \vec{H} (\vec{r})] (7)$

Ссылка [1] основы изящный способ описать неизвестные _InPO явным образом, с помощью интересного изменения метода коллокации. Во-первых, мы рассматриваем узел коллокации, который стремится к центру ребра ${\vec{r}}_{n + N_{M o M}}$ из определенной основной функции ${\vec{f}}_{n + N_{M o M}} (\vec{r})$ и находится в плюс треугольник. Мы затем умножаем Eq. (7) вектором ${\vec{t}}_{n + N_{M o M}}^{+}$ . Поскольку нормальный компонент основной функции под интересом в ребре - все до одного, другие основные функции, совместно использующие тот же треугольник, не имеют никакого нормального компонента в этом ребре, результат становится

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n + N_{M o M}}) {\vec{t}}_{n + N_{M o M}}^{+} \cdot ⌊ {\vec{n}}_{n + N_{M o M}}^{+} \times \vec{H} ({\vec{r}}_{n + N_{M o M}}) ⌋ (8a)$

Повторите ту же операцию с минус треугольник и получите

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n + N_{M o M}}) {\vec{t}}_{n + N_{M o M}}^{-} \cdot ⌊ {\vec{n}}_{n + N_{M o M}}^{-} \times \vec{H} ({\vec{r}}_{n + N_{M o M}}) ⌋ (8b)$

Add оба Eqs. (8a) и (8b) вместе, разделите результат на два и преобразуйте тройное векторное произведение, чтобы получить

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n + N_{M o M}}) \vec{H} ({\vec{r}}_{n + N_{M o M}}) \cdot (⌊ {\vec{t}}_{n + N_{M o M}}^{+} \times {\vec{n}}_{n + N_{M o M}}^{+} ⌋ + ⌊ {\vec{t}}_{n + N_{M o M}}^{-} \times {\vec{n}}_{n + N_{M o M}}^{-} ⌋) / 2 (9)$

Поэтому по данным Eqs. (2) и (3),

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n + N_{M o M}}) \vec{H} ({\vec{r}}_{n + N_{M o M}}) \cdot {\vec{l}}_{n + N_{M o M}} (10)$

Чтобы завершить деривацию, H-поле, излученное областью MoM, всегда написано в форме

$\vec{H} (\vec{r}) = \sum_{n = 1}^{N_{M o M}} {\vec{C}}_{n} (\vec{r}) I_{n}^{M o M} (11)$

где ${\vec{C}}_{n} (r)$ даны отдельными вкладами основной функции. В самом простом случае каждый такой вклад является дипольным излучением [3]. Замена Eq. (11) в Eq. (10) выражения

$\begin{array}{l} I_{n}^{P O} = \sum_{n = 1}^{N_{M o M}} {\hat{Z}}_{P O m n} I_{n}^{M o M} (12) \\ {\hat{Z}}_{P O m n} = 2 δ ({\vec{r}}_{n + N_{M o M}}) \vec{C} ({\vec{r}}_{n + N_{M o M}}) \cdot {\vec{l}}_{m + N_{M o M}} m = 1, ...., N_{P O}, n = 1, ..., N_{M o M} \end{array}$

Метод прямого решения

Согласно второй фигуре, двойная система уравнений имеет форму

$\begin{array}{l} {\hat{Z}}_{11} {\vec{I}}^{M o M} + {\hat{Z}}_{12} {\vec{I}}^{P O} = \vec{V} (13) \\ {\vec{I}}^{P O} = {\hat{Z}}_{P O} {\vec{I}}^{M o M} \end{array}$

Метод прямого решения приводит к замене выражения для ПО, текущей в первое уравнение,

$({\hat{Z}}_{11} + {\hat{Z}}_{12} {\hat{Z}}_{P O}) {\vec{I}}^{M o M} = \vec{V} (14)$

Примечание

Классическая формулировка физической оптики (PO) не поддерживает несколько отражений от физической структуры, освещенной плоской волной. Плотность тока ПО допустима только в освещенной области структуры. Эта формулировка не обрабатывает отражений из освещенной области, которые приводят к вторичному освещению различной области структуры.

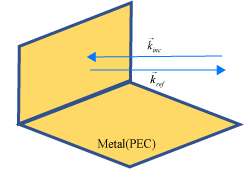
Случай 1: Когда направление инцидентной плоской волны приводит к отражению назад в направлении входящего источника.
Случай 2: Когда угол инцидентной плоской волны вызывает второе отражение от другой части структуры, это отражение значительно способствует рассеянному полю и не быть рассмотренным решателем ПО.

Ссылки

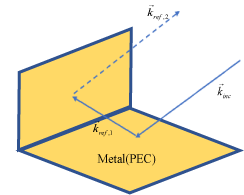
[1] У. Джейкобус и Ф. М. Лэндсторфер, “Улучшенная Формулировка MM По для Рассеивания от 3D Отлично Проводящих Тел Произвольной Формы”, Сделка IEEE. Антенны и Распространение, издание AP-43, № 2, стр 162-169, февраль 1995.

[2] С. М. Рао, Д. Р. Вилтон и А. В. Глиссон, “Электромагнитное рассеивание поверхностями произвольной формы”, Сделка IEEE. Антенны и Распространение, издание AP-30, № 3, стр 409-418, май 1982.

[3] С. Макаров, антенна и моделирование EM в MATLAB, Вайли, Нью-Йорк, 2002.

Документация

Гибридный метод MoM-PO для металлических антенн с большими рассеивателями