Используя инструменты Mathworks, можно создать интерполяционные таблицы для внутреннего контроллера постоянного магнита синхронного двигателя (PMSM), который характеризует d-ось и q-ось, текущую как функция потока q-оси и d-оси.
Чтобы сгенерировать параметры потока для блока Flux-Based PMSM, выполните эти шаги рабочего процесса. Скрипт в качестве примера CreatingIdqTable.m вызовы gridfit смоделировать текущую поверхность с помощью рассеянных или полурассеянных данных о потоке.
| Рабочий процесс | Описание |
|---|---|
|
Загрузите и предварительно обработайте эти нелинейные моторные данные о потоке из тестирования динамометра или анализа конечных элементов (FEA):
| |
|
Используйте | |
|
Установите переменные рабочей области, которые можно использовать для параметров блоков Flux-Based PM Controller. |
Загрузите и предварительно обработайте эти нелинейные моторные данные о потоке из тестирования динамометра или анализа конечных элементов (FEA):
d-и q-текущая ось
d-и q-поток оси
Электромагнитный крутящий момент двигателя
Откройте скрипт в качестве примера CreatingIdqTable.m.
Загрузите и предварительно обработайте данные.
% Load the data from a |mat| file captured from a dynamometer or % another CAE tool. load FEAdata.mat;
Определите минимальные и максимальные значения потока.
flux_d_min = min(min(FEAdata.flux.d)) ; flux_d_max = max(max(FEAdata.flux.d)) ; flux_q_min = min(min(FEAdata.flux.q)) ; flux_q_max = max(max(FEAdata.flux.q)) ;
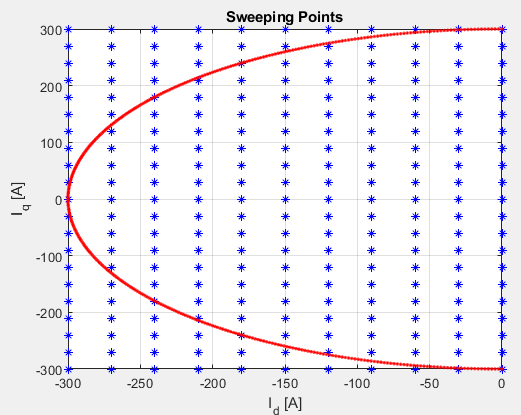
Постройте широкие текущие точки, используемые, чтобы собрать данные.
for i = 1:length(FEAdata.current.d) for j = 1:1:length(FEAdata.current.q) plot(FEAdata.current.d(i),FEAdata.current.q(j),'b*'); hold on end end
Постройте текущие предельные точки развертки и круг.
for angle_theta = pi/2:(pi/2/200):(3*pi/2) plot(300*cos(angle_theta),300*sin(angle_theta),'r.'); hold on end xlabel('I_d [A]') ylabel('I_q [A]') title('Sweeping Points'); grid on; xlim([-300,0]); ylim([-300,300]); hold off
Таблицы потока и могут иметь различные размеры шага для токов. Равномерно разрядка строк и столбцов помогает улучшить точность интерполяции. Этот скрипт использует интерполяцию сплайна.
Установите интервал для строк таблицы и столбцов.
% Set the spacing for the table rows and columns
flux_d_size = 50;
flux_q_size = 50;Сгенерируйте линейные расположенные с интервалами векторы для точек останова.
% Generate linear spaced vectors for the breakpoints
ParamFluxDIndex = linspace(flux_d_min,flux_d_max,flux_d_size);
ParamFluxQIndex = linspace(flux_q_min,flux_q_max,flux_q_size);Создайте 2D декартовы координаты на основе токов q-оси и d-оси.
% Create 2-D grid coordinates based on the d-axis and q-axis currents
[id_m,iq_m] = meshgrid(FEAdata.current.d,FEAdata.current.q);Составьте таблицу для текущей d-оси.
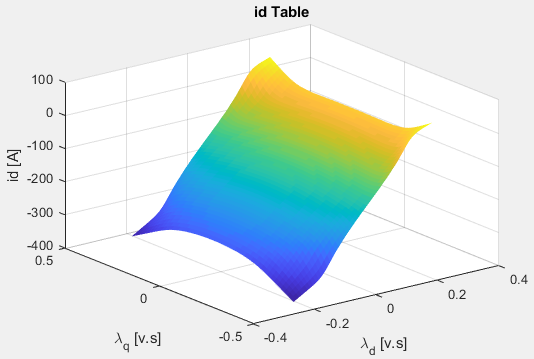
% Create the table for the d-axis current id_fit = gridfit(FEAdata.flux.d,FEAdata.flux.q,id_m,ParamFluxDIndex,ParamFluxQIndex); ParamIdLookupTable = id_fit'; figure; surf(ParamFluxDIndex,ParamFluxQIndex,ParamIdLookupTable'); xlabel('\lambda_d [v.s]');ylabel('\lambda_q [v.s]');zlabel('id [A]');title('id Table'); grid on; shading flat;
текущая d-ось, Id, как функция потока q-оси, λq, и потока d-оси, λd.
Составьте таблицу для текущей q-оси.
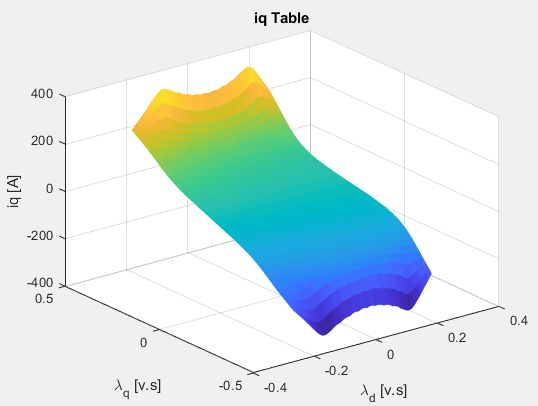
% Create the table for the q-axis current iq_fit = gridfit(FEAdata.flux.d,FEAdata.flux.q,iq_m,ParamFluxDIndex,ParamFluxQIndex); ParamIqLookupTable = iq_fit'; figure; surf(ParamFluxDIndex,ParamFluxQIndex,ParamIqLookupTable'); xlabel('\lambda_d [v.s]');ylabel('\lambda_q [v.s]');zlabel('iq [A]'); title('iq Table'); grid on; shading flat;
текущая q-ось, Iq, как функция потока q-оси, λq, и потока d-оси, λd.
Установите параметры блоков на эти значения, присвоенные в скрипте в качестве примера.
| Параметр | MATLAB® Commands |
|---|---|
|
Vector of d-axis flux, flux_d |
flux_d=ParamFluxDIndex; |
|
Vector of q-axis flux, flux_q |
flux_q=ParamFluxQIndex; |
| Corresponding d-axis current, id |
id=ParamIdLookupTable; |
|
Corresponding q-axis current, iq |
iq=ParamIqLookupTable; |
[1] Ху, Dakai, Yazan Alsmadi и Луня Сюй. “Высокое качество нелинейное моделирование IPM на основе измеренного статора извилистое потокосцепление”. IEEE® Transactions на Промышленных Приложениях, Издании 51, № 4, июль/август 2015.
[2] Чен, Сяо, Джиэбин Ван, Bhaskar Сенатор, Панайотис Лазари, Tianfu Sun. “Высокочастотная и В вычислительном отношении Эффективная Модель для Внутренних Машин Постоянного магнита, Рассматривая Магнитное Насыщение, Пространственные Гармоники и Эффект Потери в железе”. Транзакции IEEE на Industrial Electronics, Издании 62, № 7, июль 2015.
[3] Оттоссон, J., М. Алэкула. “Компактное поле, ослабляющее реализацию контроллера”. Международный Симпозиум по Силовой электронике, Электрическим Дискам, Автоматизации и Движению, июль 2006.
Flux-Based PM Controller | Flux-Based PMSM