comm.PhaseNoise
Примените шум фазы к сгенерированному модулированному сигналу
Описание
comm.PhaseNoise Система object™ добавляет шум фазы в комплексный сигнал. Этот объект эмулирует нарушения, введенные локальным генератором передатчика радиосвязи или приемника. Объект генерирует отфильтрованный шум фазы согласно заданной спектральной маске и добавляет его во входной сигнал. Для описания моделирования шума фазы см. Алгоритмы.
Добавить шум фазы использование comm.PhaseNoise объект:
Создайте
comm.PhaseNoiseобъект и набор его свойства.Вызовите объект с аргументами, как будто это была функция.
Чтобы узнать больше, как Системные объекты работают, смотрите то, Что Системные объекты?.
Создание
Синтаксис
Описание
phznoise = comm.PhaseNoise
phznoise = comm.PhaseNoise(Name,Value)Name установите на заданный Value. Можно задать дополнительные аргументы пары "имя-значение" в любом порядке как (Name1, Value1..., NameN, ValueN).
phznoise = comm.PhaseNoise(level,offset,samplerate)
Свойства
Использование
Синтаксис
Описание
Входные параметры
Выходные аргументы
Функции объекта
Чтобы использовать объектную функцию, задайте Системный объект как первый входной параметр. Например, чтобы выпустить системные ресурсы Системного объекта под названием obj, используйте этот синтаксис:
release(obj)
Примеры
Эффекты шума фазы на 16-QAM сигнале
Добавьте вектор шума фазы и вектор смещения частоты к 16-QAM сигналу. Затем постройте сигнал.
Создайте Системный объект шума фазы.
pnoise = comm.PhaseNoise('Level',-50,'FrequencyOffset',20);
Сгенерируйте модулируемые символы.
M = 16; % From 16-QAM
data = randi([0 M-1],1000,1);
modData = qammod(data,M);Используйте pnoise применять шум фазы. Отобразите данные, которым повреждают на графике.
y = pnoise(modData); scatterplot(y)
Просмотрите эффекты шума фазы на спектре сигнала
Просмотрите эффекты шума фазы на синусоиде на 10 МГц при помощи спектра анализатор. Настройте пропускную способность разрешения спектра анализатор, чтобы видеть его удар на визуализируемый спектральный шум.
Инициализируйте переменные для симуляции.
fc = 1e6; % Carrier frequency in Hz fs = 4e6; % Sample rate in Hz. phNzLevel = [-85 -118 -125 -145]; % Phase noise level in dBc/Hz phNzFreqOff = [1e3 9.5e3 19.5e3 195e3]; % Phase noise frequency offset in Hz Nspf = 6e6; % Number of Samples per frame freqSpan = 400e3; % Frequency span in Hz for spectrum computation
Создайте синусоиду, шум фазы и спектр объекты анализатора.
sinewave = dsp.SineWave('Amplitude',1,'Frequency',fc,'SampleRate',fs, ... 'SamplesPerFrame',Nspf,'ComplexOutput',true); pnoise = comm.PhaseNoise('Level',phNzLevel, ... 'FrequencyOffset',phNzFreqOff,'SampleRate',fs); spectrumscopeRBW1 = dsp.SpectrumAnalyzer('NumInputPorts',2, ... 'SampleRate',fs,'FrequencySpan','Span and center frequency', ... 'CenterFrequency',fc,'Span',freqSpan,'RBWSource','Property', ... 'RBW',1,'SpectrumType','Power density','SpectralAverages',10, ... 'SpectrumUnits','dBW','YLimits',[-150 10], ... 'Title','Resolution Bandwidth 1 Hz','Position',[79 147 605 374]); spectrumscopeRBW10 = dsp.SpectrumAnalyzer('NumInputPorts',2, ... 'SampleRate',fs,'FrequencySpan','Span and center frequency', ... 'CenterFrequency',fc,'Span',freqSpan,'RBWSource','Property', ... 'RBW',10,'SpectrumType','Power density','SpectralAverages',10, ... 'SpectrumUnits','dBW','YLimits',[-150 10], ... 'Title','Resolution Bandwidth 10 Hz','Position',[685 146 605 376]);
Чтобы анализировать спектр и шум фазы, пример включает два спектра объекты анализатора, с пропускной способностью разрешения на 10 Гц и на 1 Гц, соответственно. Спектр объекты анализатора использует Hann по умолчанию установка работы с окнами, модули установлены в dBW/Hz, и номер спектральных средних значений определяется к 10.
x = sinewave(); y = pnoise(x);
Когда пропускная способность разрешения составляет 1 Гц, dBW/Hz просмотрите для спектра, который анализатор показывает тону в 0 dBW/Hz. Спектр объект анализатора корректирует для эффекта распространения степени работы с окнами Hann. Результаты показывают, что визуальное среднее значение шума фазы совпадает с заданным спектром шума фазы.
spectrumscopeRBW1(x,y)
Когда пропускная способность разрешения составляет 10 Гц, dBW/Hz просмотрите для спектра, который анализатор показывает тону в-10 dBW/Hz. Тональная энергия синусоиды теперь распространена через 10 Гц вместо 1 Гц, таким образом, синусоида уровень PSD уменьшает на 10 дБ. С пропускной способностью разрешения на уровне 10 Гц визуальное среднее значение шума фазы все еще достигает шума фазы, заданного объектом шума фазы.
С пропускной способностью разрешения, увеличенной от 1 Гц до 10 Гц, спектр, который объект анализатора все еще корректирует для эффекта распространения степени окна Hann, и это достигает лучшего спектрального усреднения с более широкой пропускной способностью разрешения. Для получения дополнительной информации смотрите Почему Windows Использования?.
spectrumscopeRBW10(x,y)
Вычислите шум фазы RMS в градусах между чистыми и шумными синусоидами. В общем случае чистый сигнал должен быть временем, выровненным с сигналом с шумом, чтобы точно определить ошибку фазы. Однако в этом случае периодичность синусоиды делает этот шаг ненужным.
ph_err = unwrap(angle(y) - angle(x));
rms_ph_nz_deg = rms(ph_err)*180/pi();
sprintf('The computed RMS phase noise is %3.2f degrees.\n',rms_ph_nz_deg)ans =
'The computed RMS phase noise is 0.18 degrees.
'
Алгоритмы
Выходной сигнал, y k, связан, чтобы ввести последовательность x k y k=xkejφk, где φ k является шумом фазы. Шум фазы отфильтрован Гауссов шум, таким образом, что φ k=f (n k), где n k является шумовой последовательностью и f, представляет операцию фильтрации.
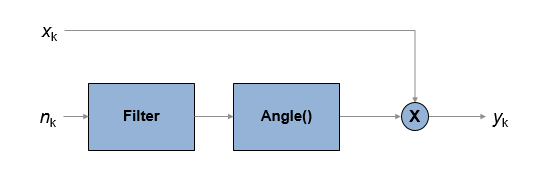
Чтобы смоделировать шум фазы, задайте характеристику маски плотности спектра мощности (PSD) путем определения скалярных или векторных значений для смещения частоты и уровня шума фазы.
Для скалярного смещения частоты и спецификации уровня шума фазы, БИХ-цифровой фильтр вычисляет маску спектра. Маска спектра имеет 1/f характеристику, которая проходит через заданную точку.
Для векторного смещения частоты и спецификации уровня шума фазы, КИХ-фильтр вычисляет маску спектра. Маска спектра интерполирована через log10 (f). Это плоско от DC до самого низкого смещения частоты, и от самого высокого смещения частоты до половины частоты дискретизации.
БИХ-цифровой фильтр
Для БИХ-цифрового фильтра коэффициент числителя
где смещение f является смещением частоты в Гц, и L является уровнем шума фазы в дБн/Гц. Коэффициенты знаменателя, γ i, рекурсивно определяются как
где γ 1 = 1, i = {1, 2..., N t}, и N t является количеством коэффициентов фильтра. N t является степенью 2 от 27 к 219. Значение N t растет, когда смещение шума фазы уменьшается к 0 Гц.
КИХ-фильтр
Для КИХ-фильтра уровень шума фазы определяется через log10 (f) интерполяция для смещений частоты в области значений [df, f s / 2], где df является разрешением частоты, и f s является частотой дискретизации. Шум фазы является плоским от 0 Гц до самого маленького смещения частоты, и от самого большого смещения частоты до f s / 2. Разрешение частоты равно , где N t является количеством коэффициентов и является степенью 2 меньше чем или равных 216. Если N t <28, КИХ-фильтр области времени используется. В противном случае КИХ-фильтр частотного диапазона используется.
Алгоритм увеличивает N t, пока эти условия не соблюдают:
Разрешение частоты меньше минимального значения вектора смещения частоты.
Разрешение частоты меньше минимального различия между двумя последовательными частотами в векторе смещения частоты.
Максимальным количеством КИХ-касаний фильтра является
216.
Ссылки
[1] Kasdin, N. J. "Дискретная Симуляция Цветных Шумовых и Стохастических процессов и 1 / (f^alpha); Генерация Шума Закона о Степени". Продолжения IEEE. Издание 83, № 5, май 1995, стр 802–827.