kalman

Проект фильтра Калмана, Оценка состояния фильтра Калмана

Синтаксис

[kest,L,P] = kalman(sys,Qn,Rn,Nn) [kest,L,P] = kalman(sys,Qn,Rn,Nn,sensors,known) [kest,L,P,M,Z] = kalman(sys,Qn,Rn,...,type)

Описание

kalman проектирует средство оценки состояния Фильтра Калмана или Кальмана, учитывая модель в пространстве состояний объекта и данных о ковариации шума процесса и измерения. Оценка состояния фильтра Калмана предоставляет оптимальное решение следующих непрерывных или дискретных проблем оценки.

Оценка непрерывного времени

Учитывая непрерывный объект

$\begin{array}{l} \dot{x} = A x + B u + G w (состояние уравнение) \\ y = C x + D u + H w + v (измерение уравнение) \end{array}$

с известными входными параметрами u, белый шум процесса w и белый шум измерения удовлетворение v

$E (w) = E (v) = 0, E (w w^{T}) = Q, E (v v^{T}) = R, E (w v^{T}) = N$

создайте оценку состояния $\hat{x} (t)$ это минимизирует установившуюся ошибочную ковариацию
$P = \lim_{t \to \infty}$ $E ({x - \hat{x}} {x - \hat{x}}^{T})$

Оптимальным решением является Фильтр Калмана уравнениями

$\begin{array}{l} \dot{\hat{x}} = A \hat{x} + B u + L (y - C \hat{x} - D u) \\ [\begin{matrix} \hat{y} \\ \hat{x} \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} + [\begin{matrix} D \\ 0 \end{matrix}] u \end{array}$

Усиление фильтра L определяется путем решения алгебраического уравнения Riccati, чтобы быть

$L = (P C^{T} + \bar{N}) {\bar{R}}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

и P решает соответствующее алгебраическое уравнение Riccati.

Средство оценки использует известные входные параметры u и измерения y, чтобы сгенерировать выход и оценки состояния $\hat{y}$ и $\hat{x}$ . Обратите внимание на то, что $\hat{y}$ оценивает истинный объект выход

$y = C x + D u + H w + v$

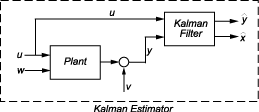
Оценка дискретного времени

Учитывая дискретный объект

$\begin{array}{l} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

и шумовые данные о ковариации

$E (w [n] w {[n]}^{T}) = Q, E (v [n] v {[n]}^{T}) = R, E (w [n] v {[n]}^{T}) = N$

Средство оценки имеет следующее уравнение состояния:

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + B u [n] + L (y [n] - C \hat{x} [n | n - 1] - D u [n])$

Матрица усиления L выведена путем решения дискретного уравнения Riccati, чтобы быть

$L = (A P C^{T} + \bar{N}) {(C P C^{T} + \bar{R})}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

Существует два варианта Оценок состояния фильтра Калмана дискретного времени:

Текущее средство оценки генерирует выходные оценки $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ . Это средство оценки имеет выходное уравнение

$[\begin{matrix} \hat{y} [n | n] \\ \hat{x} [n | n] \end{matrix}] = [\begin{matrix} (I - M_{y}) C \\ I - M_{x} C \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} (I - M_{y}) D & M_{y} \\ - M_{x} D & M_{x} \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}],$
где инновации получают _Mx, и _My заданы как:

$\begin{matrix} M_{x} = P C^{T} {(C P C^{T} + \bar{R})}^{- 1}, \\ M_{y} = (C P C^{T} + H Q H^{T} + H N) {(C P C^{T} + \bar{R})}^{- 1} . \end{matrix}$
_Mx обновляет предсказание $\hat{x} [n | n - 1]$ использование нового измерения $y [n]$ .

$\hat{x} [n | n] = \hat{x} [n | n - 1] + M_{x} \underset{i n n o v a t i o n}{\underset{︸}{(y [n] - C \hat{x} [n | n - 1] - D u [n])}} .$
Когда H = 0, $M_{y} = C M_{x}$ и $y [n | n] = C x [n | n] + D u [n]$ .
Задержанное средство оценки генерирует выходные оценки $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до _yv [n –1]. Это средство оценки легче реализовать внутренние циклы управления и имеет выходное уравнение

$[\begin{matrix} \hat{y} [n | n - 1] \\ \hat{x} [n | n - 1] \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} D & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}]$

[kest,L,P] = kalman(sys,Qn,Rn,Nn) создает модель в пространстве состояний kest из Оценки состояния фильтра Калмана, учитывая модель объекта управления sys и шумовые данные о ковариации Qn, Rn, Nn (матрицы Q, R, N, описанный в Описании). sys должна быть модель в пространстве состояний с матрицами $A, [B G], C, [D H]$ .

Получившееся средство оценки kest имеет входные параметры $[u; y]$ и выходные параметры $[\hat{y}; \hat{x}]$ (или их дубликаты дискретного времени). Можно не использовать последний входной параметр Nn когда N = 0.

Функциональный kalman решает и непрерывные и дискретные проблемы и производит непрерывное средство оценки когда sys непрерывно и дискретное средство оценки в противном случае. В непрерывное время, kalman также возвращается, Кальман получают L и установившаяся ошибочная ковариационная матрица PP решает связанное уравнение Riccati.

[kest,L,P] = kalman(sys,Qn,Rn,Nn,sensors,known) обрабатывает более общую ситуацию когда

Не все выходные параметры sys измеряются.
Входные параметры воздействия w не являются последними входными параметрами sys.

Векторы индекса sensors и known задайте который выходные параметры y sys измеряются и который вводит u, известны (детерминированные). Все другие входные параметры sys приняты стохастические.

[kest,L,P,M,Z] = kalman(sys,Qn,Rn,...,type) задает тип средства оценки для объектов дискретного времени sys. type аргументом является любой 'current' (значение по умолчанию) или 'delayed'. Для объектов дискретного времени, kalman возвращает средство оценки, и инновации получают L и M и установившиеся ошибочные ковариации

$\begin{array}{l} P = \lim_{n \to \infty} E (e [n | n - 1] e [^{n | n - 1] T}), e [n | n - 1] = x [n] - x [n | n - 1] \\ Z = \lim_{n \to \infty} E (e [n | n] e [^{n | n] T}), e [n | n] = x [n] - x [n | n] \end{array}$

Примеры

См. Проект LQG для оси X и Кальмана Филтеринга для примеров, которые используют kalman функция.

Ограничения

Объект и шумовые данные должны удовлетворить:

(C, A) обнаруживаемый
$\bar{R} > 0$ и $\bar{Q} - \bar{N} {\bar{R}}^{- 1} {\bar{N}}^{T} \geq 0$
$(A - \bar{N} {\bar{R}}^{- 1} C, \bar{Q} - \bar{N} {\bar{R}}^{- 1} {\bar{N}}^{T})$ не имеет никакого неконтролируемого режима на мнимой оси (или модульный круг в дискретное время) с обозначением

$\begin{array}{l} \bar{Q} = G Q G^{T} \\ \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

Ссылки

[1] Франклин, G.F., степень доктора юридических наук Пауэлл и M.L. Рабочий, цифровое управление динамических систем, второго выпуска, Аддисона-Уэсли, 1990.

[2] Льюис, F., оптимальная оценка, John Wiley & Sons, Inc, 1986.

[3] Deshpande, A.S., "Устраняя Разрыв в Прикладном Кальмане Филтеринге: Оценка Выводит, Когда Измерения Коррелируются с Шумом Процесса". Журнал Систем управления IEEE, Издание 37, Номер 3, 2017, стр 87–93.

Документация

kalman

Синтаксис

Описание

Примеры

Ограничения

Ссылки

Смотрите также

Темы

Документация Control System Toolbox

Поддержка