Документация

Серийные нейронные сети задержки времени проектирования

Начните с самой прямой динамической сети, которая состоит из сети прямого распространения с коснувшейся линией задержки во входе. Это называется фокусируемой нейронной сетью с временной задержкой (FTDNN). Это - часть общего класса динамических сетей, названных фокусируемыми сетями, в которых движущие силы появляются только на входном слое статической многоуровневой сети прямого распространения. Следующая фигура иллюстрирует 2D слой FTDNN.

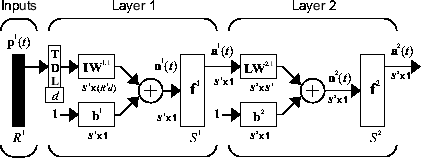
Эта сеть хорошо подходит для предсказания timeseries. Следующий пример использование FTDNN для предсказания классических временных рядов.

Следующая фигура является графиком нормированных данных об интенсивности, зарегистрированных от Далекого Инфракрасного Лазера в хаотичном состоянии. Это - часть одного из нескольких наборов данных, используемых для Соревнования Временных рядов Санта-Фе [WeGe94]. На соревновании цель состояла в том, чтобы использовать первые 1 000 точек временных рядов, чтобы предсказать следующие 100 точек. Поскольку наша цель состоит в том, чтобы просто проиллюстрировать, как использовать FTDNN для предсказания, сеть обучена здесь, чтобы выполнить предсказания "один шаг вперед". (Можно использовать получившуюся сеть для многоступенчатых вперед предсказаний, кормя предсказаниями назад вход сети и продолжая выполнять итерации.)

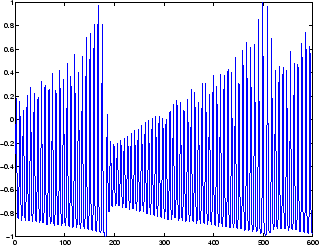
Первый шаг должен загрузить данные, нормировать их и преобразовать их в последовательность времени (представленный массивом ячеек):

y = laser_dataset;
y = y(1:600);

Теперь создайте сеть FTDNN, с помощью timedelaynet команда. Эта команда похожа на feedforwardnet команда, с дополнительным входом коснувшегося вектора линии задержки (первый вход). В данном примере используйте коснувшуюся линию задержки с задержками от 1 до 8 и используйте десять нейронов в скрытом слое:

ftdnn_net = timedelaynet([1:8],10);
ftdnn_net.trainParam.epochs = 1000;
ftdnn_net.divideFcn = '';

Расположите сетевые входные параметры и цели для обучения. Поскольку сеть имеет коснувшуюся линию задержки задержка имеющая 8, начните путем предсказания девятого значения временных рядов. Также необходимо загрузить коснувшуюся линию задержки с восемью начальными значениями временных рядов (содержавшийся в переменной Pi):

p = y(9:end);
t = y(9:end);
Pi=y(1:8);
ftdnn_net = train(ftdnn_net,p,t,Pi);

Заметьте, что вход к сети совпадает с целью. Поскольку сеть имеет минимальную задержку одного временного шага, это означает, что вы выполняете предсказание "один шаг вперед".

Во время обучения появляется следующее учебное окно.

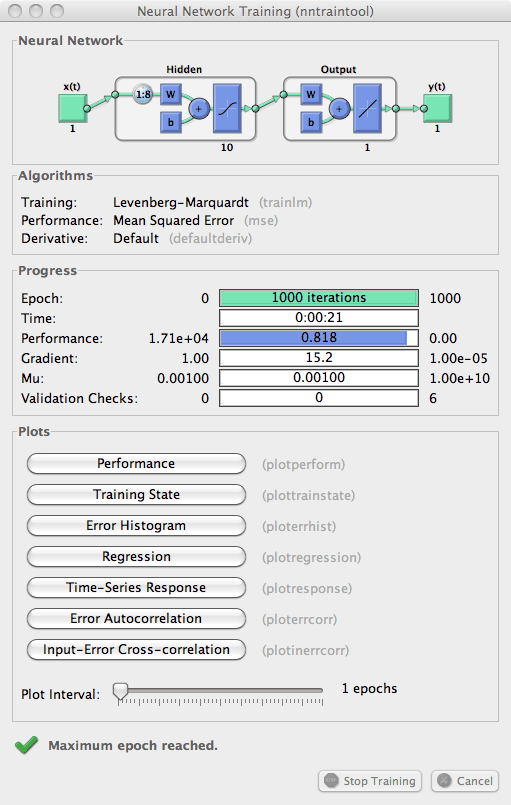
Обучение остановилось, потому что максимальная эпоха была достигнута. Из этого окна можно отобразить ответ сети путем нажатия на Time-Series Response. Следующая фигура появляется.

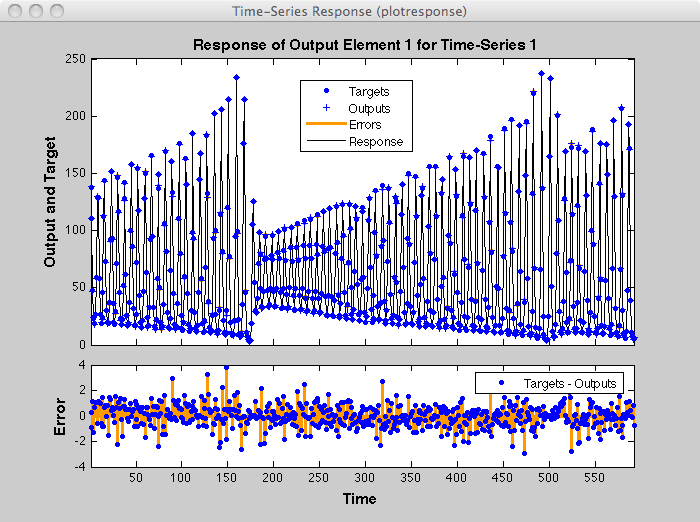
Теперь симулируйте сеть и определите ошибку предсказания.

yp = ftdnn_net(p,Pi);
e = gsubtract(yp,t);
rmse = sqrt(mse(e))

rmse =
    0.9740

(Обратите внимание на то, что gsubtract общая функция вычитания, которая может работать с массивами ячеек.) Этот результат намного лучше, чем вы, возможно, получили использование линейного предиктора. Можно проверить это со следующими командами, которые проектируют линейный фильтр с тем же коснувшимся входом линии задержки как предыдущий FTDNN.

lin_net = linearlayer([1:8]);
lin_net.trainFcn='trainlm';
[lin_net,tr] = train(lin_net,p,t,Pi);
lin_yp = lin_net(p,Pi);
lin_e = gsubtract(lin_yp,t);
lin_rmse = sqrt(mse(lin_e))

lin_rmse =
	21.1386

rms ошибка 21.1386 для линейного предиктора, но 0.9740 для нелинейного предиктора FTDNN.

Одна хорошая функция FTDNN - то, что он не требует, чтобы динамическая обратная связь вычислила сетевой градиент. Это вызвано тем, что коснувшаяся линия задержки появляется только во входе сети и не содержит обратной связи или корректируемых параметров. Поэтому вы найдете, что эта сеть обучается быстрее, чем другие динамические сети.

Если у вас есть приложение для динамической сети, попробуйте линейную сеть сначала (linearlayer) и затем FTDNN (timedelaynet). Если никакая сеть не является удовлетворительной, попробуйте одну из более комплексных динамических сетей, обсужденных в остатке от этой темы.

Каждый раз нейронная сеть обучена, может привести к различному решению из-за различного начального веса и сместить значения и различные деления данных в обучение, валидацию и наборы тестов. В результате различные нейронные сети, обученные на той же проблеме, могут дать различные выходные параметры для того же входа. Чтобы гарантировать, что нейронная сеть хорошей точности была найдена, переобучайтесь несколько раз.

Существует несколько других методов для того, чтобы улучшить начальные решения, если более высокая точность желаема. Для получения дополнительной информации смотрите, Улучшают Мелкое Обобщение Нейронной сети и Стараются не Сверхсоответствовать.

p = y(9:end);
t = y(9:end);
Pi = y(1:8);

[p,Pi,Ai,t] = preparets(ftdnn_net,y,y);

[X,Xi,Ai,T,EW,shift] = preparets(net,inputs,targets,feedback,EW)