Документация

Симуляция с параллельными входными параметрами в статической сети

Самая простая ситуация для симуляции сети происходит, когда сеть, которая будет симулирована, является статической (не имеет никакой обратной связи или задержек). В этом случае вы не должны быть обеспокоены тем, происходят ли входные векторы в последовательности определенного времени, таким образом, можно обработать входные параметры как параллельные. Кроме того, проблема сделана еще более простой путем предположения, что сеть имеет только один входной вектор. Используйте следующую сеть в качестве примера.

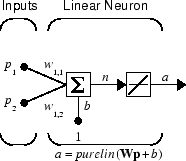
Чтобы настроить эту линейную сеть прямого распространения, используйте следующие команды:

net = linearlayer;
net.inputs{1}.size = 2;
net.layers{1}.dimensions = 1;

Для простоты присвойте матрицу веса и смещение, чтобы быть W = [1 2] и b = [0].

Команды для этих присвоений

net.IW{1,1} = [1 2];
net.b{1} = 0;

Предположим, что сетевой набор данных моделирования состоит из Q = 4 параллельных вектора:

Параллельные векторы представлены сети как одна матрица:

P = [1 2 2 3; 2 1 3 1];

Можно теперь симулировать сеть:

A = net(P)
A =
     5     4     8     5

Одна матрица параллельных векторов представлена сети, и сеть производит одну матрицу параллельных векторов, как выведено. Результатом было бы то же самое, если бы было четыре сети, действующие параллельно и каждый, какая сеть получила один из входных векторов и произвела одни из выходных параметров. Упорядоченное расположение входных векторов не важно, потому что они не взаимодействуют друг с другом.

Симуляция с последовательными входными параметрами в динамической сети

Когда сеть содержит задержки, вход к сети обычно был бы последовательностью входных векторов, которые происходят в определенном порядке времени. Чтобы проиллюстрировать этот случай, следующий рисунок показывает простую сеть, которая содержит одну задержку.

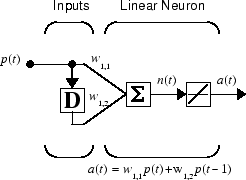
Следующие команды создают эту сеть:

net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;

Присвойте матрицу веса, чтобы быть W = [1 2].

Команда:

net.IW{1,1} = [1 2];

Предположим, что входная последовательность:

Последовательные входные параметры представлены сети как элементы массива ячеек:

P = {1 2 3 4};

Можно теперь симулировать сеть:

A = net(P)
A = 
    [1]    [4]    [7]    [10]

Вы вводите массив ячеек, содержащий последовательность входных параметров, и сеть производит массив ячеек, содержащий последовательность выходных параметров. Порядок входных параметров важен, когда они представлены как последовательность. В этом случае текущая производительность получена путем умножения текущего входа на 1 и предыдущего входа 2 и подведения итогов результата. Если бы необходимо было изменить порядок входных параметров, числа, полученные в выходе, изменились бы.

Симуляция с параллельными входными параметрами в динамической сети

Если бы необходимо было применить те же входные параметры как набор параллельных входных параметров вместо последовательности входных параметров, вы получили бы совершенно другой ответ. (Однако не ясно, почему вы хотели бы сделать это с динамической сетью.) Это было бы, как будто каждый вход был применен одновременно к отдельной параллельной сети. Для предыдущего примера, Симуляции с Последовательными Входными параметрами в Динамической Сети, если вы используете параллельный набор входных параметров, вы имеете

который может быть создан со следующим кодом:

P = [1 2 3 4];

Когда вы симулируете с параллельными входными параметрами, вы получаете

A = net(P)
A =
     1     2     3     4

Результат эквивалентен, если вы одновременно применили каждые из входных параметров к отдельной сети и вычислили ту выход. Обратите внимание на то, что, потому что вы не присваивали начальных условий сетевым задержкам, они были приняты, чтобы быть 0. Для этого случая выход является просто 1 раз входом, потому что вес, который умножает текущий вход, равняется 1.

В определенных особых случаях вы можете хотеть симулировать сетевой ответ на несколько различных последовательностей одновременно. В этом случае вы хотели бы подарить сети параллельный набор последовательностей. Например, предположите, что вы хотели представить следующие две последовательности сети:

Вход P должен быть массив ячеек, где каждый элемент массива содержит два элемента двух последовательностей, которые происходят одновременно:

P = {[1 4] [2 3] [3 2] [4 1]};

Можно теперь симулировать сеть:

A = net(P);

Получившийся сетевой выход был бы

A = {[1 4] [4 11] [7 8] [10 5]}

Как вы видите, первый столбец каждой матрицы составляет выходную последовательность, произведенную первой входной последовательностью, которая была той, используемой в более раннем примере. Второй столбец каждой матрицы составляет выходную последовательность, произведенную второй входной последовательностью. Между двумя параллельными последовательностями нет никакого взаимодействия. Это - как будто они были каждый применены, чтобы разделить сети, запускающиеся параллельно.

Следующая схема показывает общий формат для сетевого входа P когда существует Q параллельные последовательности временных шагов TS. Это покрывает все случаи, где существует один входной вектор. Каждым элементом массива ячеек является матрица параллельных векторов, которые соответствуют тому же моменту времени для каждой последовательности. Если будет несколько входных векторов, будет несколько строк матриц в массиве ячеек.

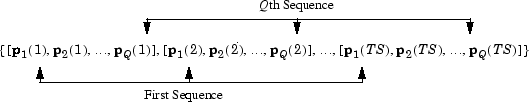
В этой теме вы применяете последовательные и параллельные входные параметры к динамическим сетям. В Симуляции с Параллельными Входными параметрами в Статической Сети вы применили параллельные входные параметры к статическим сетям. Также возможно применить последовательные входные параметры к статическим сетям. Это не изменяет симулированный отклик сети, но это может влиять на путь, которым обучена сеть. Это станет ясным в Концепциях Обучения Нейронной сети.

См. также Конфигурируют Мелкие Вводы и выводы Нейронной сети.