Программное обеспечение Fixed-Point Designer™ помогает вам спроектировать и преобразовать свои алгоритмы в фиксированную точку. Проектируете ли вы просто алгоритмы фиксированной точки в MATLAB® или используете Fixed-Point Designer в сочетании с продуктами генерации кода MathWorks®, эти лучшые практики помогают вам добраться от типового кода MATLAB до эффективной реализации фиксированной точки. Эти лучшые практики также покрыты этим вебинаром: Ручной Вебинар Лучшых практик Преобразования Фиксированной точки
Лучшая практика для структурирования вашего кода состоит в том, чтобы разделить ваш основной алгоритм от другого кода, который вы используете, чтобы протестировать и проверить результаты. Создайте тестовый файл, чтобы вызвать ваш исходный алгоритм MATLAB и версии фиксированной точки алгоритма. Например, как показано в следующей таблице, вы можете настроить некоторые входные данные, чтобы питаться в ваш алгоритм, и затем, после того, как вы обработаете те данные, создадите некоторые графики проверить результаты. Поскольку необходимо преобразовать только алгоритмический фрагмент в фиксированную точку, более эффективно структурировать код так, чтобы у вас был тестовый файл, в котором вы создаете свои входные параметры, вызываете ваш алгоритм и строите результаты и один (или больше) алгоритмические файлы, в которых вы делаете базовую обработку.
| Оригинальный код | Лучшая практика | Модифицированный код |
|---|---|---|
% TEST INPUT
x = randn(100,1);
% ALGORITHM
y = zeros(size(x));
y(1) = x(1);
for n=2:length(x)
y(n)=y(n-1) + x(n);
end
% VERIFY RESULTS
yExpected=cumsum(x);
plot(y-yExpected)
title('Error')
| Проблема Генерация тестового воздействия и верификация результатов смешиваются с кодом алгоритма. Фиксация Создайте тестовый файл, который является отдельным от вашего алгоритма. Поместите алгоритм в его собственную функцию. | Тестовый файл % TEST INPUT
x = randn(100,1);
% ALGORITHM
y = cumulative_sum(x);
% VERIFY RESULTS
yExpected = cumsum(x);
plot(y-yExpected)
title('Error')
Алгоритм в его собственной функции function y = cumulative_sum(x)
y = zeros(size(x));
y(1) = x(1);
for n=2:length(x)
y(n) = y(n-1) + x(n);
end
end
|
Можно использовать тестовый файл для:
Проверьте, что ваш алгоритм с плавающей точкой ведет себя, как вы ожидаете, прежде чем вы преобразуете его в фиксированную точку. Поведение алгоритма с плавающей точкой является базовой линией, с которой вы сравниваете поведение версий фиксированной точки вашего алгоритма.
Предложите типы данных с фиксированной точкой.
Сравните поведение версий фиксированной точки вашего алгоритма к базовой линии с плавающей точкой.
Ваши тестовые файлы должны осуществить алгоритм в его полном рабочем диапазоне так, чтобы области значений симуляции были точны. Например, для фильтра, реалистические входные параметры являются импульсами, суммами синусоид и сигналами щебета. С этими входными параметрами, с помощью линейной теории, можно проверить, что выходные параметры правильны. Сигналы, которые производят максимальный выход, полезны для проверки, что ваша система не переполняется. Качество предложенных типов данных с фиксированной точкой зависит от того, как хорошо тестовые файлы покрывают рабочий диапазон алгоритма с точностью, которую вы хотите.
Используя Fixed-Point Designer, вы можете:
Оснастите свой код и предоставьте предложения по типу данных помочь вам преобразовать свой алгоритм в фиксированную точку, с помощью следующих функций:
buildInstrumentedMex, который генерирует скомпилированный код С, который включает инструментирование логгирования.
showInstrumentationResults, который показывает результаты, регистрируемые оснащенным, скомпилированным кодом С.
clearInstrumentationResults, который очищается, регистрируемое инструментирование следует из памяти.
Ускорьте свои алгоритмы фиксированной точки путем создания файла MEX с помощью fiaccel функция.
Любые алгоритмы MATLAB, которые вы хотите к инструментальному использованию buildInstrumentedMex и любые алгоритмы фиксированной точки, что вы хотите ускорить использование fiaccel должен выполнить требования генерации кода и правила. Чтобы просмотреть подмножество языка MATLAB, который поддерживается для генерации кода, смотрите Функции и Объекты, Поддержанные для Генерации кода C/C++.
Чтобы помочь вам идентифицировать неподдерживаемые функции или построения в вашем коде MATLAB, используйте один из следующих инструментов.
Добавьте %#codegen прагма к верхней части вашего файла MATLAB. Анализатор кода MATLAB отмечает функции и построения, которые не доступны в подмножестве языка MATLAB, поддержанного для генерации кода. Этот совет появляется в режиме реального времени, когда вы редактируете свой код в редакторе MATLAB.
Для получения дополнительной информации смотрите, что Контрольный код Использует Анализатор кода MATLAB.
Используйте инструмент Code Generation Readiness, чтобы сгенерировать статический отчет относительно вашего кода. Отчет идентифицирует вызовы функций и использования типов данных, которые не поддерживаются для генерации кода. Сгенерировать отчет для функции, myFunction1, в командной строке введите coder.screener('myFunction1').
Для получения дополнительной информации смотрите, что Контрольный код Использует Инструмент Готовности Генерации кода.
Прежде чем вы запустите свое преобразование фиксированной точки, идентифицируете, какие функции, используемые в вашем алгоритме, не поддерживаются для фиксированной точки. Рассмотрите, как вы можете заменить их или в противном случае изменить вашу реализацию, которая будет более оптимизирована для целевых процессоров. Например, вы можете должны быть найти (или записать ваше собственное) замены для функций как log2, fft, и exp. Другие функции как sin, cos, и sqrt может поддержать фиксированную точку, но для лучшего КПД, можно хотеть рассмотреть альтернативную реализацию как интерполяционная таблица или основанный на CORDIC алгоритм.
Если вы не можете сразу найти замену, можно продолжить преобразовывать остальную часть алгоритма в фиксированную точку путем простой изоляции любых функций, которые не поддерживают фиксированную точку с броском, чтобы удвоиться во входе и брошенном к фиксированной точке при выходе.
| Оригинальный код | Лучшая практика | Модифицированный код |
|---|---|---|
y = 1/exp(x); | Проблема Фиксация Бросьте вход, чтобы удвоиться, пока у вас не будет замены. В этом случае, |
y = 1/exp(double(x)); |
(:) = синтаксис известен как преобразованное в нижний индекс присвоение. Когда вы используете этот синтаксис, MATLAB перезаписывает значение левого аргумента стороны, но сохраняет существующий размер типа данных и массива. Это особенно важно в хранении фиксированной точки переменных фиксированной точки (в противоположность непреднамеренному превращению их в, удваивается), и для предотвращения роста разрядности, когда это необходимо, чтобы обеспечить конкретный тип данных для выхода.
| Оригинальный код | Лучшая практика | Модифицированный код |
|---|---|---|
acc = 0; for n = 1:numel(x) acc = acc + x(n); end | Проблема
Фиксация Сохранить исходный тип данных |
acc = 0; for n = 1:numel(x) acc(:) = acc + x(n); end |
Для получения дополнительной информации смотрите Рост разрядности Управления.
Для инструментирования и генерации кода, создайте функцию точки входа, которая вызывает функцию, которую вы хотите преобразовать в фиксированную точку. Можно затем бросить входные параметры функции к различным типам данных. Можно добавить вызовы различных изменений функции для сравнения. При помощи функции точки входа можно запустить и фиксированную точку и варианты с плавающей точкой алгоритма. Можно также запустить различные варианты фиксированной точки. Этот подход позволяет вам выполнять итерации на вашем коде более быстро, чтобы прибыть в оптимальный проект фиксированной точки.
Этот метод преобразования фиксированной точки облегчает для вас сравнивать несколько различных реализаций фиксированной точки, и также позволяет вам легко перенастраивать свой алгоритм к различному устройству.
Разделить определения типов от вашего алгоритма:
Когда переменная будет сначала задана, используйте cast(x,'like',y) или zeros(m,n,'like',y) бросать его к вашему желаемому типу данных.
Составьте таблицу определений типов, начиная с исходных типов данных, используемых в вашем коде. Прежде, чем преобразовать в фиксированную точку, составьте таблицу типа данных, которая использует все один типы данных, чтобы найти несоответствия типов и другие проблемы.
Запустите свой код, соединенный с каждой таблицей, и посмотрите на результаты проверить связь.
| Оригинальный код | Лучшая практика | Модифицированный код |
|---|---|---|
% Algorithm n = 128; y = zeros(size(n)); | Проблема Тип данных по умолчанию в MATLAB является двойной точностью, с плавающей точкой. Фиксация
|
% Algorithm
T = mytypes('double');
n = cast(128,'like',T.n);
y = zeros(size(n),'like',T.y);
function T = mytypes(dt)
switch(dt)
case 'double'
T.n = double([]);
T.y = double([]);
case 'single'
T.n = single([]);
T.y = single([]);
end
end
|
Разделение технических требований типа данных от кода алгоритма позволяет:
Снова используйте свой код алгоритма с различными типами данных.
Сохраните свой алгоритм ненарушенным техническими требованиями типа данных и операторами switch для различных типов данных.
Улучшите удобочитаемость своего кода алгоритма.
Переключитесь между фиксированной точкой и типами данных с плавающей точкой, чтобы сравнить базовые линии.
Переключитесь между изменениями настроек фиксированной точки, не изменяя код алгоритма.
Прежде чем вы запустите преобразование, рассмотрите ваши цели по преобразованию в фиксированную точку. Вы реализуете свой алгоритм в C или HDL? Каковы ваши целевые ограничения? Ответы на эти вопросы определяют много свойств фиксированной точки, таких как доступный размер слова, дробная длина, и математические режимы, а также доступные математические библиотеки.
Создайте и запустите оснащенную MEX-функцию, чтобы получить предложения по фиксированным точкам с помощью buildInstrumentedMex и showInstrumentationResults функции. Тестовые файлы должны осуществить ваш алгоритм в его полном рабочем диапазоне. Качество предложенных типов данных с фиксированной точкой зависит от того, как хорошо тестовый файл покрывает рабочий диапазон алгоритма с точностью, которую вы хотите. Простой набор тестовых векторов не может осуществить полный спектр типов, так используйте предложения в качестве инструкции для выбора начального набора фиксированных точек и используйте ваше лучшее решение и опыт в корректировке типов. Если индексы цикла используются только в качестве индексных переменных, они автоматически преобразованы в целочисленные типы, таким образом, вы не должны явным образом преобразовывать их в фиксированную точку.
| Код алгоритма | Тестовый файл |
|---|---|
function [y,z] = myfilter(b,x,z)
y = zeros(size(x));
for n = 1:length(x)
z(:) = [x(n); z(1:end-1)];
y(n) = b * z;
end
end
|
% Test inputs
b = fir1(11,0.25);
t = linspace(0,10*pi,256)';
x = sin((pi/16)*t.^2); % Linear chirp
z = zeros(size(b'));
% Build
buildInstrumentedMex myfilter ...
-args {b,x,z} -histogram
% Run
[y,z] = myfilter_mex(b,x,z);
% Show
showInstrumentationResults myfilter_mex ...
-defaultDT numerictype(1,16) -proposeFL
|
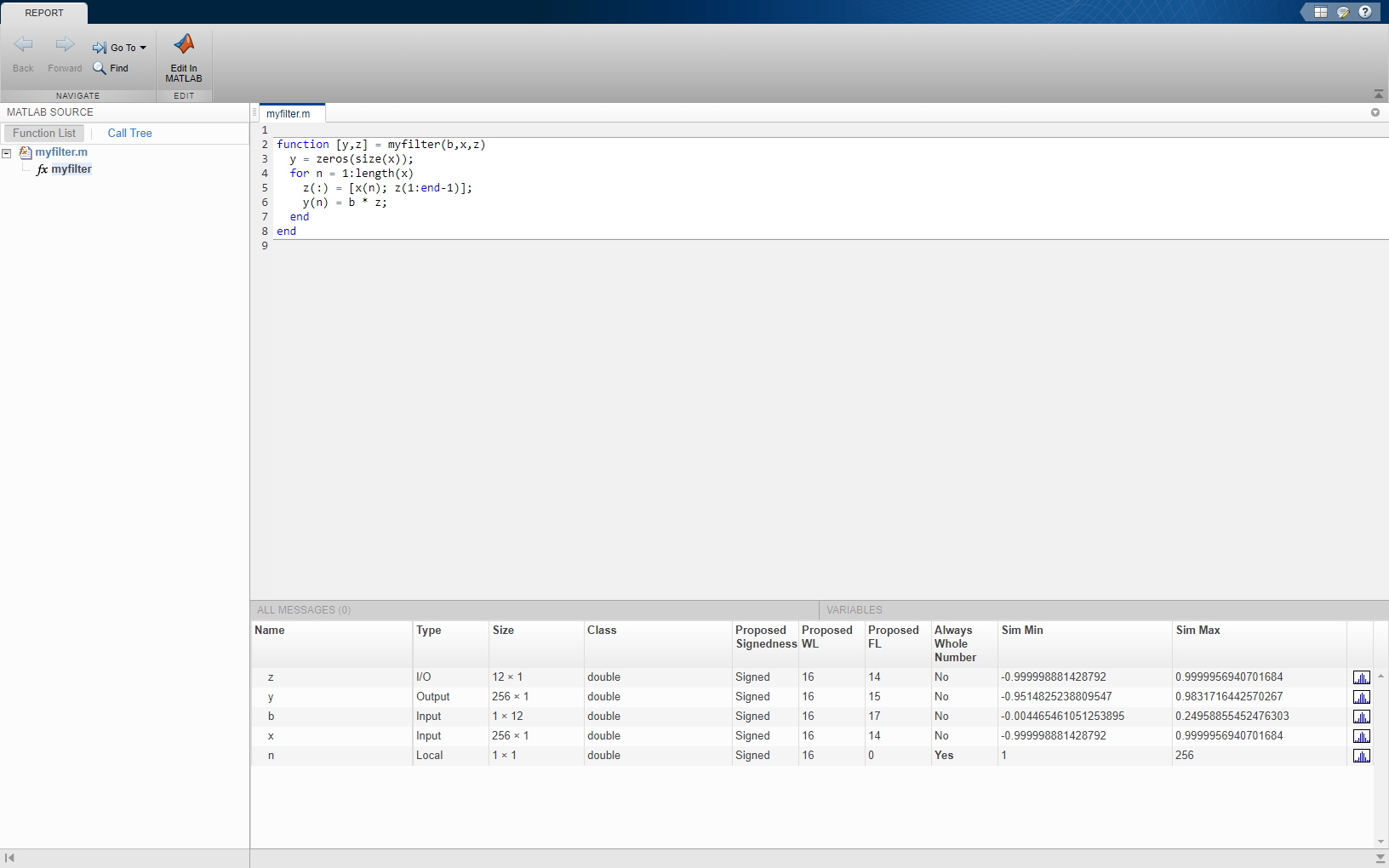
Создайте таблицу типов с помощью структуры с прототипами для переменных. Предложенные типы вычисляются из запусков симуляции. Долгая симуляция, запущенная с широким спектром ожидаемых данных, производит лучшие предложения. Можно использовать предложенные типы или использовать знание алгоритма и ограничений реализации, чтобы улучшить предложения.
Поскольку типы данных, не значения, используются, задают прототипные значения как пустые ([]).
В некоторых случаях может быть более эффективно оставить некоторые части кода в плавающей точке. Например, когда существует расширенный динамический диапазон, или та часть кода чувствительна к ошибкам округления.
| Код алгоритма | Таблицы типов | Тестовый файл |
|---|---|---|
function [y,z]=myfilter(b,x,z,T)
y = zeros(size(x),'like',T.y);
for n = 1:length(x)
z(:) = [x(n); z(1:end-1)];
y(n) = b * z;
end
end
|
function T = mytypes(dt)
switch dt
case 'double'
T.b = double([]);
T.x = double([]);
T.y = double([]);
case 'fixed16'
T.b = fi([],true,16,15);
T.x = fi([],true,16,15);
T.y = fi([],true,16,14);
end
end
|
% Test inputs
b = fir1(11,0.25);
t = linspace(0,10*pi,256)';
x = sin((pi/16)*t.^2);
% Linear chirp
% Cast inputs
T=mytypes('fixed16');
b=cast(b,'like',T.b);
x=cast(x,'like',T.x);
z=zeros(size(b'),'like',T.x);
% Run
[y,z] = myfilter(b,x,z,T);
|
Создайте тестовый файл, чтобы подтвердить это, алгоритм с плавающей точкой работает как ожидалось прежде, чем преобразовать его в фиксированную точку. Можно использовать тот же тестовый файл, чтобы предложить типы данных с фиксированной точкой и сравнить результаты фиксированной точки с базовой линией с плавающей точкой после преобразования.
Используйте масштабируемый, удваивается, чтобы обнаружить потенциальное переполнение. Масштабируемый удваивается, гибрид между числами и фиксированной точки с плавающей точкой. Fixed-Point Designer хранит их, как удваивается с масштабированием, знаком и сохраненной информацией о размере слова. Использовать масштабируемый удваивается, можно использовать свойство переопределения типа данных (DTO), или можно установить 'DataType' свойство к 'ScaledDouble' в fi или numerictype конструктор.
| К... | Использование... | Пример |
|---|---|---|
Установите переопределение типа данных локально |
|
T.a = fi([],1,16,13,'DataType', 'ScaledDouble'); a = cast(pi, 'like', T.a) a =
3.1416
DataTypeMode: Scaled double: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 13
|
Установите переопределение типа данных глобально |
|
fipref('DataTypeOverride','ScaledDoubles') T.a = fi([],1,16,13); a =
3.1416
DataTypeMode:Scaled double: binary point scaling
Signedness: Signed
WordLength:16
FractionLength:13 |
Для получения дополнительной информации смотрите Масштабированный, Удваивается.
Чтобы подстроить настройки фиксированной точки, запуститесь buildInstrumentedMex функция с –histogram отметьте и затем запустите сгенерированную MEX-функцию со своими желаемыми тестовыми воздействиями. Когда вы используете showInstrumentationResults чтобы отобразить отчет генерации кода, отчет отображает Иконку гистограммы. Кликните по значку, чтобы открыть NumericTypeScope и просмотреть распределение значений, наблюдаемых в вашей симуляции для выбранной переменной.
Переполнение, обозначенное в красном в Отчете Генерации кода, показывает во "вне области значений" интервал в NumericTypeScope. Запустите NumericTypeScope для связанной переменной или выражения путем нажатия на значок представления гистограммы![]() .
.
Если у вас есть свой первый набор типов данных с фиксированной точкой, можно затем добавить различные изменения значений фиксированной точки к таблице типов. Можно изменить и выполнить итерации, чтобы избежать переполнения, настроить дробные длины и методы округления изменения, чтобы устранить смещение.
| Код алгоритма | Таблицы типов | Тестовый файл |
|---|---|---|
function [y,z] = myfilter(b,x,z,T) y = zeros(size(x),'like',T.y); for n = 1:length(x) z(:) = [x(n); z(1:end-1)]; y(n) = b * z; end end |
function T = mytypes(dt) switch dt case 'double' T.b = double([]); T.x = double([]); T.y = double([]); case 'fixed8' T.b = fi([],true,8,7); T.x = fi([],true,8,7); T.y = fi([],true,8,6); case 'fixed16' T.b = fi([],true,16,15); T.x = fi([],true,16,15); T.y = fi([],true,16,14); end end |
function mytest % Test inputs b = fir1(11,0.25); t = linspace(0,10*pi,256)'; x = sin((pi/16)*t.^2); % Linear chirp % Run y0 = entrypoint('double',b,x); y8 = entrypoint('fixed8',b,x); y16 = entrypoint('fixed16',b,x); % Plot subplot(3,1,1) plot(t,x,'c',t,y0,'k') legend('Input','Baseline output') title('Baseline') subplot(3,2,3) plot(t,y8,'k') title('8-bit fixed-point output') subplot(3,2,4) plot(t,y0-double(y8),'r') title('8-bit fixed-point error') subplot(3,2,5) plot(t,y16,'k') title('16-bit fixed-point output') xlabel('Time (s)') subplot(3,2,6) plot(t,y0-double(y16),'r') title('16-bit fixed-point error') xlabel('Time (s)') end function [y,z] = entrypoint(dt,b,x) T = mytypes(dt); b = cast(b,'like',T.b); x = cast(x,'like',T.x); z = zeros(size(b'),'like',T.x); [y,z] = myfilter(b,x,z,T); end |
fimath свойства задают правила для выполнения арифметических операций на fi объекты, включая математику, округление и свойства переполнения. Можно использовать fimath
ProductMode и SumMode свойства сохранить естественные типы данных для C и HDL. KeepLSB установка для ProductMode и SumMode моделирует поведение целочисленных операций на языке C, в то время как KeepMSB моделирует поведение многих устройств DSP. Различные методы округления требуют различных сумм служебного кода. Установка RoundingMethod свойство к Floor, то, которое эквивалентно дополнительному усечению two, обеспечивает самую эффективную реализацию округления. Точно так же стандартный метод для обработки переполнения состоит в том, чтобы перенести использование арифметика по модулю. Другие методы обработки переполнения создают дорогостоящую логику. Каждый раз, когда возможно, устанавливает OverflowAction к Wrap.
| КОД MATLAB | Лучшая практика | Сгенерированный код C |
|---|---|---|
% Code being compiled function y = adder(a,b) y = a + b; end With types defined with default fimath settings: T.a = fi([],1,16,0); T.b = fi([],1,16,0); a = cast(0,'like',T.a); b = cast(0,'like',T.b); | Проблема Дополнительный код сгенерирован, чтобы реализовать переполнение насыщения, самое близкое округление и арифметику полной точности. |
int adder(short a, short b)
{
int y;
int i;
int i1;
int i2;
int i3;
i = a;
i1 = b;
if ((i & 65536) != 0) {
i2 = i | -65536;
} else {
i2 = i & 65535;
}
if ((i1 & 65536) != 0) {
i3 = i1 | -65536;
} else {
i3 = i1 & 65535;
}
i = i2 + i3;
if ((i & 65536) != 0) {
y = i | -65536;
} else {
y = i & 65535;
}
return y;
}
|
Код скомпилирован function y = adder(a,b) y = a + b; end С типами, заданными с fimath настройками, которые совпадают с вашими типами процессора: F = fimath(... 'RoundingMethod','Floor', ... 'OverflowAction','Wrap', ... 'ProductMode','KeepLSB', ... 'ProductWordLength',32, ... 'SumMode','KeepLSB', ... 'SumWordLength',32); T.a = fi([],1,16,0,F); T.b = fi([],1,16,0,F); a = cast(0,'like',T.a); b = cast(0,'like',T.b); | Фиксация Чтобы сделать сгенерированный код более эффективным, выберите математические настройки фиксированной точки, которые совпадают с вашими типами процессора. |
int adder(short a, short b)
{
return a + b;
}
|
Некоторые встроенные функции MATLAB могут быть сделаны более эффективными для реализации фиксированной точки. Например, можно заменить встроенную функцию на реализацию Интерполяционной таблицы или реализацию CORDIC, которая требует только итеративных операций shift-add.
Часто, деление не полностью поддерживается оборудованием и может привести к медленной обработке. Когда ваш алгоритм потребует деления, рассмотрите заменяющий его на одну из следующих опций:
Используйте перемену бита, когда знаменатель будет степенью двойки. Например, bitsra(x,3) вместо x/8.
Умножьтесь инверсией, когда знаменатель будет постоянным. Например, x*0.2 вместо x/5.
Для более эффективного кода устраните переменные с плавающей точкой. Одним исключением к этому являются индексы цикла, потому что они обычно становятся целочисленными типами.