Триангуляции часто используются, чтобы представлять 2D и 3-D геометрические области в областях применения, таких как компьютерная графика, физическое моделирование, географические информационные системы, медицинская обработка изображений и т.д. Многоугольник карты показан здесь
может быть представлен триангуляцией на карте, показанной ниже.
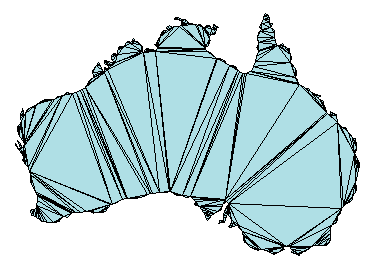
Триангуляция разлагает комплексный многоугольник на набор более простых треугольных многоугольников. Можно использовать эти многоугольники для разработки геометрических алгоритмов или графических приложений.
Точно так же можно представлять контур 3-D геометрической области с помощью триангуляции. Фигура ниже показов выпуклая оболочка набора точек в трехмерном пространстве. Каждый фасет оболочки является треугольником.
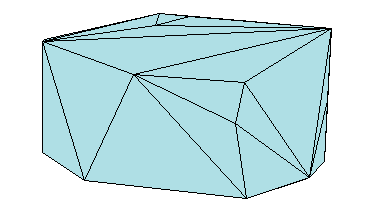
MATLAB® использует матричный формат, чтобы представлять триангуляции. Этот формат имеет две части:
Вершины, представленные как матрица, в которой каждая строка содержит координаты точки в триангуляции.
Возможность соединения триангуляции, представленная как матрица, в которой каждая строка задает треугольник или четырехгранник.
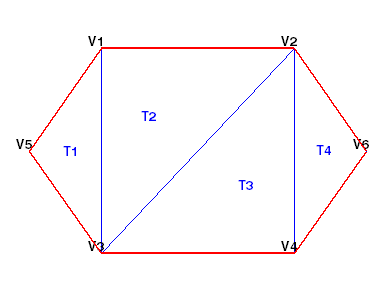
Этот рисунок показывает простую 2D триангуляцию.
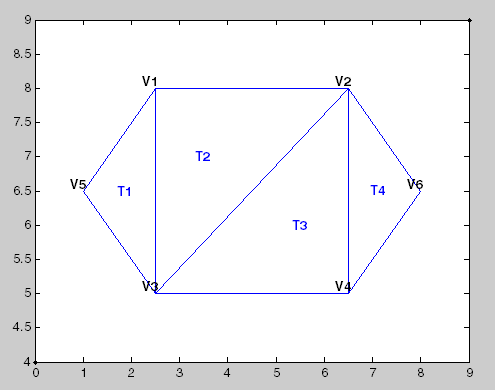
Следующая таблица показывает информацию о вершине.
| Вершины | ||
|---|---|---|
| ID вершины | x- | y- |
| V1 | 2.5 | 8.0 |
| V2 | 6.5 | 8.0 |
| V3 | 2.5 | 5.0 |
| V4 | 6.5 | 5.0 |
| V5 | 1.0 | 6.5 |
| V6 | 8.0 | 6.5 |
Данные в предыдущей таблице хранятся как матрица в среде MATLAB. Идентификаторы вершины являются метками, используемыми для идентификации определенных вершин. Они, как показывают, иллюстрируют концепцию ID вершины, но они не хранятся явным образом. Вместо этого номера строк матрицы служат идентификаторами вершины.
Данные о возможности соединения триангуляции показывают в этой таблице.
| Возможность соединения | |||
|---|---|---|---|
| Треугольный ID | Идентификаторы ограничения вершин | ||
| T1 | 5 | 3 | 1 |
| T2 | 3 | 2 | 1 |
| T3 | 3 | 4 | 2 |
| T4 | 4 | 6 | 2 |
Данные в этой таблице хранятся как матрица в среде MATLAB. Треугольные идентификаторы являются метками, используемыми для идентификации определенных треугольников. Они, как показывают, иллюстрируют концепцию треугольного ID, но они не хранятся явным образом. Вместо этого номера строк матрицы служат треугольными идентификаторами.
Вы видите тот треугольный T1 задан тремя вершинами, {V5, V3, V1}. Точно так же T4 задан вершинами, {V4, V6, V2}. Этот формат расширяет естественно к более высоким размерностям, которые требуют дополнительных столбцов данных. Например, четырехгранник в трехмерном пространстве задан четырьмя вершинами, каждая из которых имеют три координаты, (x, y, z).
Можно представлять и запросить следующие типы использования триангуляций MATLAB:
2D триангуляции, состоящие из треугольников, ограниченных вершинами и ребрами
3-D поверхностные триангуляции, состоящие из треугольников, ограниченных вершинами и ребрами
3-D триангуляции, состоящие из тетраэдров, ограниченных вершинами, ребрами и поверхностями
Матричный формат обеспечивает компактный низкий уровень, основанное на массиве представление для триангуляций. Когда вы используете триангуляции, чтобы разработать алгоритмы, вам может быть нужно больше информации о геометрических свойствах, топологии и информации о смежности.
Например, вы можете вычислить треугольные центры вписанной окружности прежде, чем построить аннотируемую триангуляцию, показанную ниже. В этом случае вы используете центры вписанной окружности, чтобы отобразить треугольные метки (T1, T2, и т.д.) в каждом треугольнике. Если вы хотите построить контур красного цвета, необходимо определить ребра, на которые ссылается только один треугольник.
Можно использовать triangulation создать представление в оперативной памяти любых 2D или 3-D данных о триангуляции, которые находятся в матричном формате, таком как матричный выход от delaunay функционируйте или другие программные инструменты. Когда ваши данные представлены с помощью triangulation, можно выполнить топологические и геометрические запросы, которые можно использовать, чтобы разработать геометрические алгоритмы. Например, можно прилагается треугольники или тетраэдры к вершине, те, которые совместно используют ребро, их центры описанной окружности и другие функции.
Можно создать triangulation одним из двух способов:
Передайте существующие данные, которые вы имеете в матричном формате к triangulation. Этими данными может быть выход от функции MATLAB, такой как delaunay или convhull. Также можно импортировать данные о триангуляции, которые были созданы другим программным обеспечением. Когда вы работаете с импортированными данными, быть уверенными ссылки на данные возможности соединения массив вершины, использующий индексацию на основе 1 вместо индексации на основе 0.
Передайте набор точек к delaunayTriangulation. Получившаяся Триангуляция Делоне является специальным видом triangulation. Это означает, что можно выполнить любой triangulation запросите на своих данных, а также любом Delaunay-специфичном запросе. В более формальных терминах языка MATLAB, delaunayTriangulation подкласс triangulation.
Создание триангуляции из Матричных Данных
В этом примере показано, как использовать матричные данные о триангуляции, чтобы создать триангуляцию, исследовать то, что это, и исследуйте то, что это может сделать.
Создайте матрицу, P, это содержит данные о вершине.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];Задайте возможность соединения, T.
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];Создайте triangulation из этих данных.
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Доступ к свойствам в triangulation таким же образом вы получаете доступ к полям struct. Например, исследуйте Points свойство, которое содержит координаты вершин.
TR.Points
ans = 6×2
2.5000 8.0000
6.5000 8.0000
2.5000 5.0000
6.5000 5.0000
1.0000 6.5000
8.0000 6.5000
Затем исследуйте возможность соединения.
TR.ConnectivityList
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Points и ConnectivityList свойства задают матричные данные для триангуляции.
triangulation класс является оберткой вокруг матричных данных. Реальная выгода является полноценностью triangulation методы класса. Методы похожи на функции, которые принимают triangulation и другие соответствующие входные данные.
triangulation класс обеспечивает простой способ индексировать в ConnectivityList матрица свойства. Доступ к первому треугольнику в триангуляции.
TR.ConnectivityList(1,:)
ans = 1×3
5 3 1
Другим способом получить первый треугольник является TR(1,:).
Исследуйте первую вершину первого треугольника.
TR(1,1)
ans = 5
Исследуйте вторую вершину первого треугольника.
TR(1,2)
ans = 3
Теперь исследуйте все треугольники в триангуляции.
TR(:,:)
ans = 4×3
5 3 1
3 2 1
3 4 2
4 6 2
Используйте triplot построить triangulation. triplot функцией не является triangulation метод, но это принимает и может построить triangulation.
figure
triplot(TR)
axis equal
Используйте triangulation метод, freeBoundary, запрашивать свободный контур и подсвечивать его в графике. Этот метод возвращает ребра триангуляции, которые совместно используются только одним треугольником. Возвращенные ребра описываются в терминах идентификаторов вершины.
boundaryedges = freeBoundary(TR)';
Теперь постройте граничные ребра как красную линию.
hold on plot(P(boundaryedges,1),P(boundaryedges,2),'-r','LineWidth',2) hold off

Можно использовать freeBoundary метод, чтобы подтвердить триангуляцию. Например, если бы вы наблюдали красные ребра во внутренней части триангуляции, затем это указало бы на проблему в том, как треугольники соединяются.
Создание триангуляции Используя delaunayTriangulation
В этом примере показано, как создать Триангуляцию Делоне с помощью delaunayTriangulation.
Когда вы создаете Триангуляцию Делоне с помощью delaunayTriangulation класс, вы автоматически получаете доступ к triangulation методы, потому что delaunayTriangulation подкласс triangulation.
Создайте delaunayTriangulation от набора точек.
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
DT = delaunayTriangulation(P)DT =
delaunayTriangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Constraints: []
Получившийся delaunayTriangulation объект имеет свойства, Points и ConnectivityList, точно так же, как triangulation объект.
Можно получить доступ к триангуляции, использующей прямую индексацию, точно так же, как triangulation. Например, исследуйте возможность соединения первого треугольника.
DT(1,:)
ans = 1×3
5 3 1
Затем исследуйте возможность соединения целой триангуляции.
DT(:,:)
ans = 4×3
5 3 1
3 4 1
1 4 2
4 6 2
Используйте triplot функционируйте, чтобы построить триангуляцию.
triplot(DT)
axis equal
Родительский класс, triangulation, обеспечивает incenter метод, чтобы вычислить центры вписанной окружности каждого треугольника.
IC = incenter(DT)
IC = 4×2
1.8787 6.5000
3.5000 6.0000
5.5000 7.0000
7.1213 6.5000
Возвращенное значение, IC, массив координат, представляющих центры вписанной окружности треугольников.
Теперь используйте центры вписанной окружности, чтобы найти положения для размещения треугольных меток на графике.
hold on numtri = size(DT,1); trilabels = arrayfun(@(P) {sprintf('T%d', P)}, (1:numtri)'); Htl = text(IC(:,1),IC(:,2),trilabels,'FontWeight','bold', ... 'HorizontalAlignment','center','Color','blue'); hold off

Вместо того, чтобы создать Триангуляцию Делоне с помощью delaunayTriangulation, вы могли использовать delaunay функция, чтобы создать данные о возможности соединения триангуляции, и затем передать данные о возможности соединения triangulation. Например,
P = [ 2.5 8.0
6.5 8.0
2.5 5.0
6.5 5.0
1.0 6.5
8.0 6.5];
T = delaunay(P);
TR = triangulation(T,P);
IC = incenter(TR);Оба подхода допустимы в этом примере, но если вы хотите создать Триангуляцию Делоне и выполнить запросы на нем, затем необходимо использовать delaunayTriangulation по этим причинам:
delaunayTriangulation класс обеспечивает дополнительные методы, которые полезны для работы с триангуляциями. Например, вы можете, чтобы выполнить ближайшего соседа и поисковые запросы точки в треугольнике.
Это позволяет вам редактировать триангуляцию, чтобы добавить, переместить, или удалить точки.
Это позволяет вам создавать ограниченные Триангуляции Делоне. Это позволяет вам создавать триангуляцию для 2D области.
delaunay | delaunayTriangulation | freeBoundary | triangulation | triplot