Извлеките ненулевые диагонали и создайте разреженную полосу и диагональные матрицы
Создайте трехдиагональную матрицу с помощью трех векторов, измените некоторые матричные диагонали, и затем извлеките диагонали.
Создайте 9 1 вектор из единиц, и затем создайте трехдиагональную матрицу с помощью вектора. Просмотрите элементы матрицы.
n = 9; e = ones(n,1); A = spdiags([e -2*e e],-1:1,n,n); full(A)
ans = 9×9
-2 1 0 0 0 0 0 0 0
1 -2 1 0 0 0 0 0 0
0 1 -2 1 0 0 0 0 0
0 0 1 -2 1 0 0 0 0
0 0 0 1 -2 1 0 0 0
0 0 0 0 1 -2 1 0 0
0 0 0 0 0 1 -2 1 0
0 0 0 0 0 0 1 -2 1
0 0 0 0 0 0 0 1 -2
Измените значения на основном (d = 0) диагональ A.
Bin = abs(-(n-1)/2:(n-1)/2)'; d = 0; A = spdiags(Bin,d,A); full(A)
ans = 9×9
4 1 0 0 0 0 0 0 0
1 3 1 0 0 0 0 0 0
0 1 2 1 0 0 0 0 0
0 0 1 1 1 0 0 0 0
0 0 0 1 0 1 0 0 0
0 0 0 0 1 1 1 0 0
0 0 0 0 0 1 2 1 0
0 0 0 0 0 0 1 3 1
0 0 0 0 0 0 0 1 4
Наконец, восстановите диагонали A как столбцы в матрице.
Bout = spdiags(A); full(Bout)
ans = 9×3
1 4 0
1 3 1
1 2 1
1 1 1
1 0 1
1 1 1
1 2 1
1 3 1
0 4 1
Извлеките ненулевые диагонали матрицы и исследуйте выходной формат spdiags.
Создайте матрицу, содержащую соединение ненулевых и нулевых диагоналей.
A = [0 5 0 10 0 0
0 0 6 0 11 0
3 0 0 7 0 12
1 4 0 0 8 0
0 2 5 0 0 9];Извлеките ненулевые диагонали из матрицы. Задайте два выходных параметров, чтобы возвратить диагональные числа.
[Bout,d] = spdiags(A)
Bout = 5×4
0 0 5 10
0 0 6 11
0 3 7 12
1 4 8 0
2 5 9 0
d = 4×1
-3
-2
1
3
Столбцы первого выхода Bout содержите ненулевые диагонали A. Второй выход d перечисляет индексы ненулевых диагоналей A. Самая длинная ненулевая диагональ в A находится в столбце 3 Bout. Дать все столбцы Bout та же длина, другие ненулевые диагонали A добавьте дополнительные нули в их соответствующие столбцы в Bout. Для m- n матрицы с m < n, правила:
Для ненулевых диагоналей ниже основной диагонали A, дополнительные нули добавляются в верхних частях столбцов (как в первых двух столбцах Bout).
Для ненулевых диагоналей выше основной диагонали A, дополнительные нули добавляются в нижних частях столбцов (как в последнем столбце Bout).
spdiags клавиатуры Bout с нулями этим способом, даже если самая длинная диагональ не возвращена в Bout.
Создайте случайную матрицу 5 на 5.
A = randi(10,5,5)
A = 5×5
9 1 2 2 7
10 3 10 5 1
2 6 10 10 9
10 10 5 8 10
7 10 9 10 7
Извлеките основную диагональ и первые диагонали выше и ниже его.
d = [-1 0 1]; Bout = spdiags(A,d)
Bout = 5×3
10 9 0
6 3 1
5 10 10
10 8 10
0 7 10
Попытайтесь извлечь пятую супердиагональ (d = 5). Поскольку A имеет только четыре супердиагонали, spdiags возвращает диагональ как все нули той же длины как основное (d = 0) диагональ.
B5 = spdiags(A,5)
B5 = 5×1
0
0
0
0
0
Исследуйте как spdiags создает диагонали, когда столбцы входной матрицы более длинны, чем диагонали, они заменяют.
Создайте 6 7 матрица чисел 1 - 6.
Bin = repmat((1:6)',[1 7])
Bin = 6×7
1 1 1 1 1 1 1
2 2 2 2 2 2 2
3 3 3 3 3 3 3
4 4 4 4 4 4 4
5 5 5 5 5 5 5
6 6 6 6 6 6 6
Используйте spdiags создать квадрат 6 6 матрица с несколькими из столбцов Bin как диагонали. Поскольку некоторые диагонали только имеют один или два элемента, существует несоответствие в размерах между столбцами в Bin и диагонали в A.
d = [-4 -2 -1 0 3 4 5]; A = spdiags(Bin,d,6,6); full(A)
ans = 6×6
1 0 0 4 5 6
1 2 0 0 5 6
1 2 3 0 0 6
0 2 3 4 0 0
1 0 3 4 5 0
0 2 0 4 5 6
Каждый из столбцов в Bin имеет шесть элементов, но только основную диагональ в A имеет шесть элементов. Поэтому все другие диагонали в A обрежьте элементы в столбцах Bin так, чтобы они соответствовали на выбранных диагоналях:
Путем spdiags обрезает диагонали, зависит от размера m- n матричный Aкогда , поведение как изображено выше:
Диагонали ниже основных диагональных элементов взятия от верхних частей столбцов сначала.
Диагонали выше основных диагональных элементов взятия от нижних частей столбцов сначала.
Это поведение инвертирует когда :
A = spdiags(Bin,d,5,6); full(A)
ans = 5×6
1 0 0 1 1 1
2 2 0 0 2 2
3 3 3 0 0 3
0 4 4 4 0 0
5 0 5 5 5 0
Диагонали выше основных диагональных элементов взятия от верхних частей столбцов сначала.
Диагонали ниже основных диагональных элементов взятия от нижних частей столбцов сначала.
A — Введите матрицуВведите матрицу. Эта матрица обычно (но не обязательно) разреженна.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного числа: Да
d — Диагональные числаДиагональные числа в виде скаляра или вектора из положительных целых чисел. Диагональные числа следуют тем же соглашениям как diag:
d < 0 ниже основной диагонали и удовлетворяет d >= -(m-1).
d = 0 основная диагональ.
d > 0 выше основной диагонали и удовлетворяет d <= (n-1).
m- n матричный A имеет (m + n - 1) диагонали. Эти диагонали заданы в векторном d использование индексов от -(m-1) к (n-1). Например, если A 5 6, это имеет 10 диагоналей, которые заданы в векторном d использование индексов-4,-3... 4, 5. Следующая схема иллюстрирует эту диагональную нумерацию.
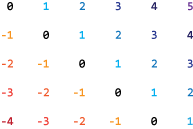
Если вы задаете диагональ, которая находится за пределами A (такие как d = 7 в примере выше), затем spdiags возвращает ту диагональ как все нули.
Пример: spdiags(A,[3 5]) извлекает третьи и пятые диагонали из A.
Bin — Диагональные элементыДиагональные элементы в виде матрицы. Эта матрица обычно (но не обязательно) полна. spdiags использует столбцы Bin заменять заданные диагонали в A. Если требуемым размером выхода является m- n, затем Bin должен иметь min(m,n) столбцы.
С синтаксисом S = spdiags(Bin,d,m,n), если столбец Bin имеет больше элементов, чем диагональ, которую это заменяет, и m >= nто spdiags берет элементы супердиагоналей от более низкой части столбца Bin, и элементы поддиагоналей от верхней части столбца Bin. Однако, если m < n , затем супердиагонали от верхней части столбца Bin, и поддиагонали от более низкой части. Для примера этого поведения см. Столбцы и Диагонали Различных Размеров.
Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного числа: Да
mN — Размеры размерностиРазмеры размерности в виде неотрицательных скалярных целых чисел. spdiags использование эти входные параметры, чтобы определить, как большой матрица, чтобы создать.
Пример: spdiags(Bin,d,300,400) создает 300 400 матрица со столбцами B помещенный по заданным диагоналям d.