fgoalattainРассмотрите разработку фильтра Конечной импульсной характеристики (FIR) линейной фазы. Проблема состоит в том, чтобы спроектировать фильтр lowpass с величиной один на всех частотах между 0 и 0,1 Гц и нуле величины между 0.15 и 0,5 Гц.
Частотная характеристика H (f) для такого фильтра задана
| (1) |
где A (f) является величиной частотной характеристики. Одно решение состоит в том, чтобы применить целевой метод достижения к величине частотной характеристики. Учитывая функцию, которая вычисляет величину, fgoalattain попытается варьироваться коэффициенты величины a (n), пока ответ величины не будет совпадать с желаемым ответом в некотором допуске. Функция, которая вычисляет ответ величины, дана в filtmin.m. Эта функция использует a, коэффициенты функции величины и w, дискретизация частотного диапазона интереса.
Чтобы настроить целевую проблему достижения, необходимо задать goal и weights для проблемы. Для частот между 0 и 0.1, целью является та. Для частот между 0,15 и 0.5, целью является нуль. Частоты между 0,1 и 0.15 не заданы, таким образом, никакие цели или веса не необходимы в этой области значений.
Эта информация хранится в переменной goal переданный fgoalattain. Длина goal совпадает с длиной, возвращенной функциональным filtmin. Так, чтобы целям одинаково удовлетворили, обычно weight был бы установлен в abs(goal). Однако, поскольку некоторыми целями является нуль, эффект использования weight=abs(goal) обеспечит цели с weight 0, чтобы быть удовлетворенным как трудные ограничения и цели с weight 1 возможно, чтобы быть underattained (см. Целевой Метод Достижения). Поскольку все цели близки в величине, с помощью weight из единицы для всех целей отдаст им равный приоритет. (Используя abs(goal) поскольку веса более важны когда величина goal отличается более значительно.) Кроме того, устанавливая
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal)); указывает, что каждая цель должна быть почти возможной к своему целевому значению (ни больше, ни меньше, чем).
function y = filtmin(a,w) n = length(a); y = cos(w'*(0:n-1)*2*pi)*a ;
% Plot with initial coefficients
a0 = ones(15,1);
incr = 50;
w = linspace(0,0.5,incr);
y0 = filtmin(a0,w);
clf, plot(w,y0,'-.b');
drawnow;
% Set up the goal attainment problem
w1 = linspace(0,0.1,incr) ;
w2 = linspace(0.15,0.5,incr);
w0 = [w1 w2];
goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))];
weight = ones(size(goal));
% Call fgoalattain
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));
[a,fval,attainfactor,exitflag]=fgoalattain(@(x)filtmin(x,w0),...
a0,goal,weight,[],[],[],[],[],[],[],options);
% Plot with the optimized (final) coefficients
y = filtmin(a,w);
hold on, plot(w,y,'r')
axis([0 0.5 -3 3])
xlabel('Frequency (Hz)')
ylabel('Magnitude Response (dB)')
legend('initial', 'final')
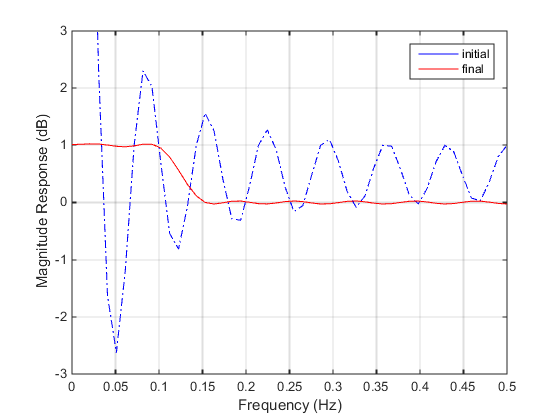
grid onСравните ответ величины, вычисленный с начальными коэффициентами и итоговыми коэффициентами (Ответ величины с Начальными и Итоговыми Коэффициентами Величины). Обратите внимание на то, что вы могли использовать firpm (Signal Processing Toolbox) функция в программном обеспечении Signal Processing Toolbox™, чтобы спроектировать этот фильтр.
Ответ величины с начальными и итоговыми коэффициентами величины