Spherical Joint
Соединение с одним сферическим примитивом
Библиотека
Соединения
Описание
Этот блок представляет соединение тремя вращательными степенями свободы. Один сферический примитив обеспечивает три вращательных степени свободы. Основа и системы координат последователя остаются совпадающими в процессе моделирования.
Объединенные степени свободы
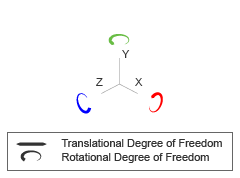
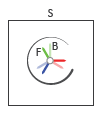
Блок шарнира представляет движение между базой и последующей системой координат как одно изменяющееся во времени преобразование. Сферический примитив (S) применяет это преобразование, которое заставляет систему координат последователя вращаться относительно базовой системы координат о произвольной 3-D оси. Этот объединенный примитив не восприимчив, чтобы установить в карданном подвесе блокировку.
Объединенное преобразование
Набор дополнительного состояния предназначается для блока руководства для каждого объединенного примитива. Цели включают положение и скорость. Приоритетный уровень устанавливает относительную важность целей состояния. Если две цели несовместимы, приоритетный уровень определяет который из целей, чтобы удовлетворить.
Внутренние параметры механики составляют аккумулирование энергии и рассеяние в каждом объединенном примитиве. Спрингское действие как элементы аккумулирования энергии, сопротивляясь любой попытке переместить объединенный примитив от его положения равновесия. Объединенные демпферы действуют как энергетические элементы рассеяния. Спрингс и демпферы строго линейны.
В почти ведущем винте и постоянных скоростных примитивах, объединенные пределы служат, чтобы обуздать область значений движения между системами координат. Объединенный примитив может иметь нижнюю границу, верхнюю границу, обоих, или, в состоянии по умолчанию, ни одном. Чтобы осуществить границы, соединение добавляет в каждого пружинный демпфер. Чем более жесткий пружина, тем тяжелее остановка или возврат, если колебания возникают. Чем более сильный демпфер, тем глубже вязкие потери, которые постепенно уменьшают колебания контакта или в сверхослабленных примитивах, мешают им формироваться в целом.
Каждый объединенный примитив имеет набор дополнительного приведения в действие и распознающихся портов. Порты приведения в действие принимают входные параметры физического сигнала, которые управляют объединенными примитивами. Эти входные параметры могут быть силами и крутящими моментами или желаемой объединенной траекторией. Распознающиеся порты предоставляют физическому сигналу выходные параметры, которые измеряют объединенное примитивное движение, а также силы приводов и крутящие моменты. Режимы приведения в действие и распознающиеся типы меняются в зависимости от объединенного примитива.
Параметры
Сферический примитив: цели состояния
Задайте желаемые начальные состояния сферического объединенного примитива и их относительных приоритетных уровней. Состояния, для которых можно предназначаться, включают положение и скорость. Используйте приоритетный уровень, чтобы помочь алгоритму блока решить, какое из состояния предназначается в модели, чтобы более точно удовлетворить, должен конфликты между ними возникать.
Даже в отсутствие целевых конфликтов состояния, истинные начальные состояния могут отличаться от заданных здесь. Такие несоответствия могут произойти из-за кинематических ограничений, являющихся результатом других частей модели. Если цели состояния нельзя удовлетворить точно, ей удовлетворяют приблизительно. Несоответствия отмечены в Средстве просмотра Переменной Simscape (в галерее Apps, нажмите Simscape Variable Viewer).
- Specify Position Target
Проверяйте, чтобы задать желаемое вращение системы координат последователя относительно базовой системы координат в начале симуляции.
- Priority
Выберите целевой приоритет состояния. Это - уровень важности, присвоенный цели состояния. Если всем целям состояния нельзя одновременно удовлетворить, приоритетный уровень определяет, каким целям удовлетворить сначала и как тесно удовлетворить им. Эта опция применяется и к целям состояния положения и скорости.
Приоритетный уровень Описание High (desired)Удовлетворите цели состояния точно Low (approximate)Удовлетворите цели состояния приблизительно Примечание
Во время сборки высокоприоритетные цели ведут себя как точные руководства. Низкоприоритетные цели ведут себя как грубые руководства.
- Value
Выберите метод, чтобы задать объединенную примитивную цель состояния.
Метод Описание NoneОграничьте базу и последующую систему координат совместно использовать ту же ориентацию. Aligned AxesУстановите вращение системы координат путем выравнивания двух осей системы координат последователя с двумя осями базовой системы координат. Standard AxisЗадайте вращение системы координат как угол о стандартной оси (x, y или z). Arbitrary AxisЗадайте вращение системы координат как угол о генерале [x, y, z] ось. Rotation SequenceЗадайте вращение системы координат как последовательность трех элементарных вращений. Rotation MatrixЗадайте вращение системы координат как предназначенную для правой руки ортогональную матрицу вращения.
Aligned AxesВыберите две пары осей системы координат основного последователя.
Параметр Описание Pair 1 Первая пара осей системы координат основного последователя, которая выровняется. Pair 2 Вторая пара осей системы координат основного последователя, чтобы выровняться. Выбор оси зависит от выборов оси Pair 1. Standard AxisВыберите стандартную ось вращения, разрешенную в базовой системе координат, и укажите, что последователь структурирует угол поворота.
Параметр Описание Axis Стандартная ось вращения (X, Y, или Z) разрешенный в базовой системе координат. Angle Угол поворота системы координат последователя приблизительно ось вращения относительно базовой системы координат. Arbitrary AxisВыберите общую 3-D ось вращения, разрешенную в базовой системе координат, и укажите, что последователь структурирует угол поворота.
Параметр Описание Axis Общая ось вращения [X Y Z] разрешенный в базовой системе координат. Angle Угол поворота системы координат последователя приблизительно ось вращения относительно базовой системы координат. Rotation SequenceЗадайте последовательность трех элементарных вращений вокруг выбранного сочетания x, y, и оси z. Эти последовательности вращения также известны как последовательности Тайта-Брайана и Эйлера. Вращения являются теми из системы координат последователя относительно системы координат, выбранной в параметре Rotate About.
Если вы устанавливаете параметр Rotate About на
Follower Frame, система координат последователя вращается о ее собственных осях. Эти оси изменяют ориентацию с каждым последовательным вращением. Если вы устанавливаете параметр Rotate About наBase Frame, система координат последователя вращается о фиксированных осях базовой системы координат.Параметр Описание Rotation About Структурируйте чьи оси, чтобы вращать систему координат последователя о. Sequence Последовательность осей, вокруг которых можно применить элементарные вращения. Angles Трехэлементный вектор с элементарными углами поворота приблизительно оси задан в параметре Sequence. Rotation MatrixЗадайте 3×3 матрица преобразования соответствующего вращения между базой и последующей системой координат. Матрица должна быть ортогональной и иметь определитель +1. Матрицей по умолчанию является
[1 0 0; 0 1 0; 0 0 1].
- Specify Velocity Target
Проверяйте, чтобы задать желаемую вращательную скорость системы координат последователя относительно базовой системы координат в начале симуляции.
- Value
Введите относительную вращательную скорость системы координат последователя против базовой системы координат, как спроектировано на осях выбранного Resolution Frame (
Followerпо умолчанию). Этот параметр требует трехэлементного вектора с [x y z] компоненты разрешенной относительной скорости.- Resolution Frame
Выберите систему координат, в которой можно разрешить компоненты скоростной цели. Система координат разрешения не является системой координат измерения — заданная скорость всегда является скоростью системы координат последователя относительно базовой системы координат. Система координат разрешения просто обеспечивает альтернативный набор осей, относительно которых можно интерпретировать относительные скоростные компоненты. Настройкой по умолчанию является
Follower.
Сферический примитив: внутренняя механика
Задайте сферическую примитивную внутреннюю механику. Это включает линейные упругие и демпфирующие силы, составляя аккумулирование энергии и рассеяние, соответственно. Чтобы проигнорировать внутреннюю механику, сохраните пружинную жесткость и значения коэффициента демпфирования в значении по умолчанию 0.
- Equilibrium Position
Выберите метод, чтобы задать пружинное положение равновесия. Положение равновесия является углом поворота между основой и системами координат порта последователя, в которых пружинный крутящий момент является нулем.
Метод Описание NoneОграничьте базу и последующую систему координат совместно использовать ту же ориентацию. Aligned AxesУстановите вращение системы координат путем выравнивания двух осей системы координат последователя с двумя осями базовой системы координат. Standard AxisЗадайте вращение системы координат как угол о стандартной оси (x, y или z). Arbitrary AxisЗадайте вращение системы координат как угол о генерале [x, y, z] ось. Rotation SequenceЗадайте вращение системы координат как последовательность трех элементарных вращений. Rotation MatrixЗадайте вращение системы координат как предназначенную для правой руки ортогональную матрицу вращения.
Aligned AxesВыберите две пары осей системы координат основного последователя.
Параметр Описание Pair 1 Первая пара осей системы координат основного последователя, которая выровняется. Pair 2 Вторая пара осей системы координат основного последователя, чтобы выровняться. Выбор оси зависит от выборов оси Pair 1. Standard AxisВыберите стандартную ось вращения, разрешенную в базовой системе координат, и укажите, что последователь структурирует угол поворота.
Параметр Описание Axis Стандартная ось вращения (X, Y, или Z) разрешенный в базовой системе координат. Angle Угол поворота системы координат последователя приблизительно ось вращения относительно базовой системы координат. Arbitrary AxisВыберите общую 3-D ось вращения, разрешенную в базовой системе координат, и укажите, что последователь структурирует угол поворота.
Параметр Описание Axis Общая ось вращения [X Y Z] разрешенный в базовой системе координат. Angle Угол поворота системы координат последователя приблизительно ось вращения относительно базовой системы координат. Rotation SequenceЗадайте последовательность трех элементарных вращений вокруг выбранного сочетания x, y, и оси z. Эти последовательности вращения также известны как последовательности Тайта-Брайана и Эйлера. Вращения являются теми из системы координат последователя относительно системы координат, выбранной в параметре Rotate About.
Если вы устанавливаете параметр Rotate About на
Follower Frame, система координат последователя вращается о ее собственных осях. Эти оси изменяют ориентацию с каждым последовательным вращением. Если вы устанавливаете параметр Rotate About наBase Frame, система координат последователя вращается о фиксированных осях базовой системы координат.Параметр Описание Rotation About Структурируйте чьи оси, чтобы вращать систему координат последователя о. Sequence Последовательность осей, вокруг которых можно применить элементарные вращения. Angles Трехэлементный вектор с элементарными углами поворота приблизительно оси задан в параметре Sequence. Rotation MatrixЗадайте 3×3 матрица преобразования соответствующего вращения между базой и последующей системой координат. Матрица должна быть ортогональной и иметь определитель +1. Матрицей по умолчанию является
[1 0 0; 0 1 0; 0 0 1].
- Spring Stiffness
Введите линейный коэффициент упругости. Это - крутящий момент, требуемый переместить объединенный примитив модульным углом. Линейный термин относится к математической форме пружинного уравнения.
Значением по умолчанию является 0. Выберите физическую единицу измерения. Значением по умолчанию являетсяN*m/deg.- Damping Coefficient
Введите линейный коэффициент демпфирования. Это - крутящий момент, требуемый обеспечить постоянную объединенную примитивную скорость вращения между базой и последующей системой координат.
Значением по умолчанию является 0. Выберите физическую единицу измерения. Значением по умолчанию являетсяN*m/(deg/s).
Сферический примитив: пределы
Ограничьте область значений движения объединенного примитива. Соединение ограничивает пружинные демпферы использования, чтобы сопротивляться перемещению мимо границ области значений. Объединенный примитив может иметь нижнюю границу, верхнюю границу, обоих, или, в состоянии по умолчанию, ни одном. Чем более жесткий пружина, тем тяжелее остановка или возврат, если колебания возникают. Чем более сильный демпфер, тем больше вязкие потери, которые постепенно уменьшают колебания контакта или в сверхослабленных примитивах, мешают им формироваться в целом.
- Specify Lower Limit
Выберите, чтобы добавить нижнюю границу в область значений движения объединенного примитива.
- Specify Upper Limit
Выберите, чтобы добавить верхнюю границу в область значений движения объединенного примитива.
- Value
Местоположение мимо, чтобы сопротивляться объединенному перемещению. Местоположение является смещением от основы до последователя, как измерено в базовой системе координат, в которой начинается контакт. Это - расстояние вдоль оси в призматических примитивах, углу об оси во вращательных примитивах и углу между двумя осями в сферических примитивах.
- Spring Stiffness
Сопротивление пружины контакта к смещению мимо объединенного предела. Пружина линейна, и ее жесткость является постоянной. Чем больше значение, тем тяжелее остановка. Пропорция пружины силам демпфера определяет, является ли остановка underdamped и подверженный колебаниям на контакте.
- Damping Coefficient
Сопротивление демпфера контакта, чтобы двинуться мимо объединенного предела. Демпфер линеен, и его коэффициент является постоянным. Чем больше значение, тем больше вязкие потери, которые постепенно уменьшают колебания контакта, если кто-либо возникает. Пропорция пружины силам демпфера определяет, является ли остановка underdamped и подверженный колебаниям на контакте.
- Transition Region
Область, по которой можно повысить силу пружинного демпфера до ее полного значения. Область является расстоянием вдоль оси в призматических примитивах, углу об оси во вращательных примитивах и углу между двумя осями в сферических примитивах.
Чем меньший область, тем более резкое начало контакта и меньшего такт требуется из решателя. В компромиссе между точностью симуляции и скоростью симуляции, уменьшая область перехода улучшает точность, в то время как расширение его улучшает скорость.
Сферический примитив: приведение в действие
Задайте опции приведения в действие для сферического объединенного примитива. Режимы приведения в действие включают Torque только. Выбор входа крутящего момента добавляет соответствующий порт физического сигнала в блок. Используйте этот порт, чтобы задать сигнал крутящего момента приведения в действие.
- Torque
Выберите источник для крутящего момента приведения в действие.
Настройкой по умолчанию является None.Установка крутящего момента приведения в действие Описание NoneНе примените крутящий момент приведения в действие. Provided by InputПримените крутящий момент приведения в действие на основе физического сигнала. Сигнал задает крутящий момент, действующий на систему координат последователя относительно базовой системы координат. Равный и противоположный крутящий момент действует на базовую систему координат. Выбирание этой опции отсоединяет дополнительные параметры. - Torque (X), Torque (Y), Torque (Z)
Выберите для того, чтобы привести в движение сферический объединенный примитив о каждой стандартной Оси декартовой системы координат (X, Y, Z) отдельно. Блок осушает соответствующие порты физического сигнала. Используйте эти порты, чтобы задать сигналы крутящего момента приведения в действие. Сигналы должны быть скалярными значениями.
- Torque (XYZ)
Выберите для того, чтобы привести в движение сферический объединенный примитив о произвольной оси [X Y Z]. Блок осушает соответствующий порт физического сигнала. Используйте этот порт, чтобы задать сигнал крутящего момента приведения в действие. Сигнал должен быть 3-D вектором.
- Frame
Выберите систему координат, чтобы разрешить сигнал крутящего момента приведения в действие в. Оси этой системы координат устанавливают направления этих X, Y, и компоненты крутящего момента Z. Настройкой по умолчанию является
Base.
Сферический примитив: обнаружение
Выберите переменные движения, чтобы распознаться в сферическом объединенном примитиве. Блок добавляет соответствующие порты физического сигнала. Используйте эти порты, чтобы вывести численные значения переменных движения.
Блок измеряет каждую переменную движения для системы координат последователя относительно базовой системы координат. Это разрешает, что переменная в системе координат разрешения, что вы выбираете из Frame выпадающий список.
| Переменные движения | Описание |
|---|---|
| Position | Кватернион, описывающий последователя, структурирует вращение относительно базовой системы координат. Коэффициенты кватерниона . Измерение является тем же самым во всех системах координат измерения. |
| Velocity (X), Velocity (Y), Velocity (Z) | Компоненты скорости вращения приблизительно X, Y, и оси Z. |
| Velocity | 3-D вектор скорости вращения с компонентами приблизительно X, Y, и оси Z. |
| Acceleration (X), Acceleration (Y), Acceleration (Z) | Угловые ускоряющие компоненты приблизительно X, Y, и оси Z. |
| Acceleration | 3-D угловой ускоряющий вектор с компонентами приблизительно X, Y, и оси Z. |
- Frame
Выберите систему координат, чтобы разрешить измерение в. Оси этой системы координат устанавливают направления X, Y, и векторные компоненты Z. Настройкой по умолчанию является
Base.
Настройка режима
Задайте режим соединения. Объединенный режим может быть нормален или разъединен в течение симуляции, или можно обеспечить входной сигнал, чтобы изменить режим во время симуляции.
- Режим
Выберите одну из следующих опций, чтобы задать режим соединения. Настройкой по умолчанию является
Normal.Метод Описание NormalСоединение обычно ведет себя в течение симуляции. DisengagedСоединение расцеплено в течение симуляции. Provided by InputЭта опция осушает порт mode, который можно соединить с входным сигналом, чтобы изменить объединенный режим во время симуляции. Объединенный режим нормален, когда входным сигналом является 0и расцепленный, когда входным сигналом является-1. Объединенный режим может изменяться много раз во время симуляции.
Составное Обнаружение Силы/Крутящего момента
Выберите составные силы и крутящие моменты, чтобы распознаться. Их измерения охватывают все объединенные примитивы и не характерны ни для одного. Они прибывают в два вида: ограничение и общее количество.
Ограничительные измерения дают сопротивление против движения на заблокированных осях соединения. В призматических соединениях, например, которые запрещают перевод на xy плоскости, то сопротивление балансирует все возмущения в направлениях X и Y. Общие измерения дают сумму по всем силам, и закручивает из-за входных параметров приведения в действие, внутренние пружины и демпферы, объединенные пределы положения и кинематические ограничения, которые ограничивают степени свободы соединения.
- Direction
Вектор, чтобы распознаться от пары реакции действия между базой и последующей системой координат. Пара является результатом третьего закона Ньютона движения, которое, для блока соединений, требует, чтобы сила или крутящий момент на системе координат последователя сопровождали равную и противоположную силу или крутящий момент на базовой системе координат. Укажите, распознаться ли, который проявленный базовой системой координат на системе координат последователя или проявленный последователем структурирует на базовой системе координат.
- Resolution Frame
Структурируйте, на котором можно разрешить векторные компоненты измерения. Системы координат с различными ориентациями дают различные векторные компоненты для того же измерения. Укажите, получить ли те компоненты от осей базовой системы координат или от осей системы координат последователя. Выбор имеет значение только в соединениях с вращательными степенями свободы.
- Constraint Force
Динамическая переменная, чтобы измериться. Ограничение обеспечивает встречный перевод на заблокированных осях соединения при разрешении его на свободных осях его примитивов. Выберите, чтобы вывести ограничительный вектор силы через порт fc.
- Constraint Torque
Динамическая переменная, чтобы измериться. Ограничение закручивает встречное вращение на заблокированных осях соединения при разрешении его на свободных осях его примитивов. Выберите, чтобы вывести ограничительный вектор крутящего момента через порт tc.
- Total Force
Динамическая переменная, чтобы измериться. Общая сила является суммой через все объединенные примитивы по всем источникам — входные параметры приведения в действие, внутренние пружины и демпферы, объединенные пределы положения и кинематические ограничения. Выберите, чтобы вывести общий вектор силы через порт ft.
- Total Torque
Динамическая переменная, чтобы измериться. Общий крутящий момент является суммой через все объединенные примитивы по всем источникам — входные параметры приведения в действие, внутренние пружины и демпферы, объединенные пределы положения и кинематические ограничения. Выберите, чтобы вывести общий вектор крутящего момента через порт tt.
Порты
Этот блок имеет два порта системы координат. Это также имеет дополнительные порты физического сигнала для определения входных параметров приведения в действие и обнаружения динамических переменных, таких как силы, крутящие моменты и движение. Вы осушаете дополнительный порт путем установки распознающегося флажка, соответствующего тому порту.
Структурируйте порты
B Базовая система координат
F Система координат последователя
Порты приведения в действие
Сферический объединенный примитив обеспечивает следующие порты приведения в действие:
t Вектор крутящего момента приведения в действие [tx, ty, tz] действующий на сферический объединенный примитив
tx, ty, tz — X, Y, и компоненты Z крутящего момента приведения в действие, действующего на сферический объединенный примитив
Обнаружение портов
Сферический примитив обеспечивает следующие порты обнаружения:
Q Ориентация сферического объединенного примитива в форме кватерниона
wx, wy, wz — X, Y, и компоненты скорости вращения Z сферического объединенного примитива
w Скорость вращения [wx, wy, wz] сферического объединенного примитива
основной обмен, bz — X, Y, и угловые ускоряющие компоненты Z сферического объединенного примитива
b Угловое ускорение [bx, by, bz] сферического объединенного примитива
tll — Закрутите должный связаться с нижним пределом сферического объединенного примитива, данного как величина со знаком вектора крутящего момента
tul — Закрутите должный связаться с верхним пределом сферического объединенного примитива, данного как величина со знаком вектора крутящего момента
Следующие порты обнаружения предоставляют составным силам и крутящим моментам, действующим на соединение:
фК Ограничительная сила
tc — Ограничительный крутящий момент
ft — Общая сила
tt — Общий крутящий момент
Порт режима
Настройка режима обеспечивает следующий порт:
режим — Значение режима соединения. Если вход равен
0, соединение обычно ведет себя. Если вход равен-1, соединение ведет себя, как расцеплено.