power_lineparam

Вычислите параметры RLC служебной линии электропередачи от ее проводниковых характеристик и геометрии башни

Синтаксис

LDATA = power_lineparam('new') LDATA = power_lineparam(LDATA) LDATA = power_lineparam('MYLINEDATA') power_lineparam(LDATA,'BLK') power_lineparam('MYLINEDATA','BLK')

Описание

LDATA = power_lineparam('new') возвращает переменную структуры параметрами геометрии линии по умолчанию. Можно использовать LDATA как переменная шаблона, чтобы сконфигурировать геометрию новой строки и вычислить параметры линии RLC.

LDATA структура с полями в этой таблице.

Поле	Описание
`comments`	Задайте комментарии пользователей, связанные с параметрами линии.
`units`	Модули параметров линии. Установите на `metric` задавать проводниковый диаметр, GMR, и диаметр пакета в сантиметрах и проводниковое положение в метрах. Установите на `English` задавать проводниковый диаметр, GMR, и диаметр пакета в дюймах и проводниковое положение в ногах. Значением по умолчанию является `metric`.
`frequency`	Частота, в герц, чтобы оценить параметры линии RLC. Значением по умолчанию является `60`.
`groundResistivity`	Наземное удельное сопротивление, в омметрах. Установите на `0` задавать отлично проводящую землю.
`Geometry`	Структура, задающая геометрию линии и проводниковые типы.
`Conductors`	Структура, задающая проводниковые характеристики для каждого типа.

Geometry структура с полями в этой таблице.

Поле	Описание
`NPhaseBundle`	Количество проводников фазы (одиночные проводники или пакеты подпроводников). Значением по умолчанию является `3`.
`NGroundBundle`	Количество заземляющих проводов (одиночные проводники или пакеты подпроводников). Значением по умолчанию является `2`.
`PhaseNumber`	1- `NPhaseBundle` + `NGroundBundle` вектор. Эта установка представляет номер фазы, которому принадлежат проводники. Несколько проводников могут иметь тот же номер фазы. Количеством фазы земли является `0`. Значением по умолчанию является `[1 2 3 0 0]`.
`X`	1- `NPhaseBundle` + `NGroundBundle` вектор. Эта установка представляет горизонтальное положение проводников в метрах или футах. Местоположение нулевого ссылочного положения произвольно. Для симметричной линии вы обычно выбираете `X = 0` в центре линии. Значением по умолчанию является `[-12 0 12 -8 8]`.
`Ytower`	1- `NPhaseBundle` + `NGroundBundle` вектор. Эта установка представляет вертикальное положение проводников (в башне) относительно земли в метрах или футах. Значением по умолчанию является `[20 20 20 33 33]`.
`Ymin`	1- `NPhaseBundle` + `NGroundBundle` вектор. Эта установка представляет вертикальное положение проводников относительно земли в середине промежутка в метрах или футах. Значением по умолчанию является `[20 20 20 33 33]`.
`ConductorType`	1- `NPhaseBundle` + `NGroundBundle` вектор. Эта установка представляет тип проводника. Числа соответствуют элементам вектора, заданного в `Conductors` структура. Значением по умолчанию является `[1 1 1 2 2]`.

Conductors структура с полями в этой таблице. Длина Conductors структура соответствует количеству проводниковых типов в ваших параметрах линии:

Поле	Описание
`Diameter`	Проводник вне диаметра, в cm. Значением по умолчанию является `[3.5500 1.2700]`.
`ThickRatio`	Отношение T/D полого проводника. T является толщиной материала проведения, и D является внешним диаметром. Этот параметр может варьироваться между `0` и `0.5`. Значение T/D `0.5` указывает на твердый проводник. Для проводников Алюминиевой укрепленной стали кабеля (ACSR) можно проигнорировать стальное ядро и рассмотреть полый алюминиевый проводник (типичные отношения T/D между `0.3` и `0.4`). Значением по умолчанию является `[0.3700 0.5000]`.
`GMR`	Геометрический средний радиус.
`Xa`	Реактивное сопротивление Xa, в Омах/км. `Значением по умолчанию является 0`.
`Res`	Проводниковое сопротивление DC, в Омах/км. Значением по умолчанию является `[0.0430 3.1060]`.
`Mur`	Проводниковая относительная проницаемость. Значением по умолчанию является `[1 1]`.
`NConductors`	Количество проводников на пакет. Значением по умолчанию является `[4 1]`.
`BundleDiameter`	Диаметр пакета, в cm или дюймах. Значением по умолчанию является `[65 0]`.
`AngleConductor1`	Угол, в градусах, который определяет положение первого проводника в пакете относительно горизонтальной линии, параллельной земле. Этот угол определяет ориентацию пакета. Значением по умолчанию является `[45 0]`.
`skinEffect`	Установите на да, чтобы включать удар частоты на проводниковом сопротивлении AC и индуктивности (эффект кожи). Если установлено в не, сопротивление сохранено постоянным в значении, заданном `Res` поле и индуктивность сохранены постоянными в значении, вычисленном в DC, с помощью `Diameter` поле и `ThickRatio` поле .

LDATA = power_lineparam(LDATA) вычисляет параметры линии RLC для геометрических параметров линии в LDATA структура. Возвращенная структура содержит и геометрические данные и вычисленные параметры линии RLC.

LDATA структура увеличивается с полями параметров линии RLC в этой таблице:

Поле	Описание
`R`	N-by-N матрица сопротивления линии, в Омах/км.
`L`	N-by-N матрица индуктивности линии, в Генри/км.
`C`	N-by-N матрица емкости линии, в Фарадах/км.
`R10`	Для трехфазной линии эта установка представляет положительную последовательность и сопротивления нулевой последовательности в Омах/км. Для шестифазовой линии (две двойных трехфазных схемы), эта установка представляет положительную последовательность и сопротивления нулевой последовательности схемы 1, взаимное сопротивление нулевой последовательности между схемой 1 и схемой 2, и положительную последовательность и сопротивления нулевой последовательности схемы 2.
`L10`	Для трехфазной линии, положительной последовательности и индуктивности нулевой последовательности, в Генри/км. Для шестифазовой линии (две двойных трехфазных схемы), эта установка представляет положительную последовательность и индуктивность нулевой последовательности схемы 1, взаимную индуктивность нулевой последовательности между схемой 1 и схемой 2, и положительную последовательность и индуктивность нулевой последовательности схемы 2.
`C10`	Для трехфазной линии эта установка представляет положительную последовательность и емкости нулевой последовательности в Фарадах/км. Для шестифазовой линии (две двойных трехфазных схемы), эта установка представляет положительную последовательность и емкости нулевой последовательности схемы 1, взаимную емкость нулевой последовательности между схемой 1 и схемой 2, и положительную последовательность и емкости нулевой последовательности схемы 2.

LDATA = power_lineparam('MYLINEDATA') вычисляет параметры линии RLC для геометрических параметров линии в заданном файле. 'MYLINEDATA' имя MAT-файла. MAT-файл должен содержать переменную структуры того же формата как LDATA переменная.

power_lineparam(LDATA,'BLK'), и power_lineparam('MYLINEDATA','BLK') загрузите параметры линии RLC в заданной Линии Раздела PI, Кабеле Раздела PI, Линии Распределенных параметров или блоке Three-Phase PI Section Line. 'BLK' путь блока.

power_lineparam функция вычисляет сопротивление, индуктивность и матрицы емкости произвольного расположения проводников служебной линии электропередачи. Для трехфазной линии также вычисляются симметричные значения RLC компонента.

Следующий рисунок показывает типичное проводниковое расположение относительно трехфазной двухконтурной линии. Эта настройка линии иллюстрирует различные параметры линии, которые вы задаете в LDATA структура.

Настройка трехфазной двухконтурной линии

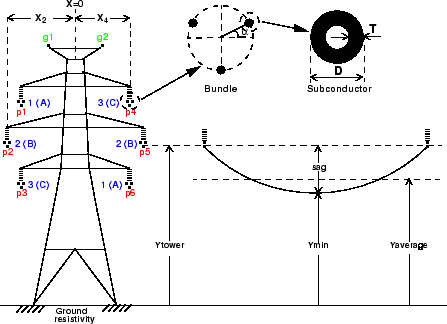
Для набора проводников N, power_lineparam вычисляет три N-by-N матрицы: серийные матрицы сопротивления и индуктивности [R] и [L] и матрица [C] емкости шунта. Эти матрицы требуются блоком Distributed Parameters Line для моделирования N - фаза асимметричные линии и однофазным блоком PI Section Line. power_lineparam также вычисляет симметричные параметры RLC компонента, требуемые блоком Three-Phase PI Section Line. Для двух двойных проводников i и k, сам и взаимные условия R, L, и матрицы C вычисляемся с помощью концепции проводников изображений [1].

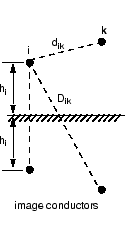
Сам и взаимные условия сопротивления:

$\begin{matrix} R_{i i} = R_{int} + Δ R_{i i} & Ω / км \end{matrix}$

$\begin{matrix} R_{i k} = Δ R_{i k} & Ω / км \end{matrix}$

Сам и взаимные условия индуктивности:

$\begin{matrix} L_{i i} = L_{int} + \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{r_{i}} + Δ L_{i i} & H / км \end{matrix}$

$\begin{matrix} L_{i k} = \frac{μ_{0}}{2 π} \cdot \log \frac{D_{i k}}{d_{i k}} + Δ L_{i k} & H / км \end{matrix}$

Сам и взаимные потенциальные содействующие условия:

$\begin{matrix} P_{i i} = \frac{1}{2 π ε_{0}} \cdot \log \frac{2 h_{i}}{r_{i}} & км / F \end{matrix}$

$\begin{matrix} P_{i k} = \frac{1}{2 π ε_{0}} \cdot \log \frac{D_{i k}}{d_{i k}} & км / F \end{matrix}$

$\begin{matrix} [C] = {[P]}^{- 1} & F / км \end{matrix}$

где:

_µ0 проницаемость свободного пространства = ^4π.10−4 H/km
_ɛ0 проницаемость свободного пространства = ^{8.8542.10−9} F/km
_ri является радиусом проводника i в метрах
_dik является расстоянием между проводниками i и k в метрах
_Dik является расстоянием между проводником i и изображением k в метрах
_привет средняя высота проводника i находящийся над землей, в метрах
Rint, Линт является внутренним сопротивлением и индуктивностью проводника
_ΔRii, _ΔRik являются условиями коррекции Карсона Р, должными основать удельное сопротивление
_ΔLii, _ΔLik являются условиями коррекции Карсона Л, должными основать удельное сопротивление

Проводниковая самоиндукция вычисляется из распространения магнитного потока внутри и снаружи проводника и производится текущим течением в самом проводнике. Часть распространения потока в материале проведения способствует внутреннему Линту индуктивности, который зависит от проводниковой геометрии. Принимая полый или твердый проводник, внутренняя индуктивность вычисляется из отношения T/D, где D является проводниковым диаметром, и T является толщиной материала проведения. Смотрите фигуру Настройка Трехфазной Двухконтурной Линии. Проводниковая самоиндукция вычисляется посредством модифицированных Функций Бесселя от проводникового диаметра, отношения T/D, удельного сопротивления и относительной проницаемости проведения материала и заданной частоты [1].

Проводниковая самоиндукция может также быть вычислена из параметров, которые обычно находятся в таблицах, предоставленных проводниковыми производителями: Геометрический средний радиус (GMR) или "Реактивное сопротивление при интервале одного фута".

GMR является радиусом эквивалентного полого проводника с нулевой толщиной, не производя внутреннего потока, давая ту же самоиндукцию. Проводниковая самоиндукция затем выведена из GMR использование следующего уравнения:

$\begin{matrix} L_{i i} = \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{G M R} + Δ L_{i i} & H / км \end{matrix}$

Для твердого проводника (T/D=0.5) GMR

$G M R = r \cdot e^{- μ_{r} / 4}$

r = радиус проводника

_μr = относительная проницаемость проведения материала

GMR, полученный из этого уравнения, принимает универсальную плотность тока в проводнике. Это предположение строго допустимо в DC. В AC GMR немного выше. Например, для твердого алюминиевого проводника 3 см диаметром (Rdc = 0.040 Ω/km), GMR увеличивается с 1,1682 см в DC к 1,1784 см на уровне 60 Гц. Производители обычно дают GMR на системной частоте номинала (50 Гц или 60 Гц).

Реактивное сопротивление _Xa при интервале 1 фута (или интервале 1 метра, если метрические модули используются) является реактивным сопротивлением положительной последовательности трехфазной линии, имеющей один фут (или один метр) располагающий с интервалами между этими тремя фазами и бесконечными проводниковыми высотами. Реактивное сопротивление при интервале 1 фута (или интервале 1 метра) на частоте f связано с GMR следующим уравнением:

$\begin{matrix} X_{a} = ω \cdot \frac{μ_{0}}{2 π} \cdot \log \frac{1}{G M R} & Ω / км \end{matrix}$

GMR = Геометрический средний Радиус в футах или метрах

ω = 2π.f в rad/s

f = частота в герц

Проводниковая матрица сопротивления на особой частоте зависит от сопротивления DC проводника, откорректированного для эффекта кожи и наземного удельного сопротивления. И матрица сопротивления и матрица индуктивности зависят от наземного удельного сопротивления и частоты. Условия коррекции для условий R и L, как разработано Дж.Р. Карсоном в 1 926 [2] реализованы в power_lineparam.

Примеры

Первый пример использует простую линию, состоящую из двух проводников, расположенных с интервалами на 1 метр на средней высоте на 8 метров выше совершенной земли (наземное удельное сопротивление _ρg= 0). Эти два проводника являются твердыми алюминиевыми проводниками (удельное сопротивление _ρc= 28.3 ¹⁰⁻⁹ Ω.m в ^20º C), которые имеют 15 мм в диаметре.

Сопротивление DC на км каждого проводника:

$\begin{matrix} r = \frac{ρ_{c} \cdot l}{A} = \frac{28.3 \times 10^{- 9} \times 1000}{π \cdot {(\frac{15 \times 10^{- 3}}{2})}^{2}} = 0.1601 & Ω / км \end{matrix}$

Когда земля, как предполагается, совершенна, недиагональные условия матрицы R являются нулем, и диагональные термины представляют проводниковые сопротивления:

$R = [\begin{matrix} 0.1601 & 0 \\ 0 & 0.1601 \end{matrix}] Ω / км$

Для твердых проводников GMR:

$\begin{matrix} G M R = r \cdot e^{- μ_{r} / 4} = \frac{1.5}{2} e^{- 1 / 4} = 0.5841 & cm \end{matrix}$

Само - и взаимная индуктивность вычисляются можно следующим образом. ΔL условия коррекции проигнорированы, потому что наземное удельное сопротивление является нулем.

$\begin{matrix} L_{11} = L_{22} = \frac{μ_{0}}{2 π} \cdot \log \frac{2 h_{i}}{G M R} = 2 \times 10^{- 4} \log \frac{2 \times 8}{0.5841 \times 10^{- 2}} = 1.583 \times 10^{- 3} H / км \\ L_{12} = L_{21} = \frac{μ_{0}}{2 π} \cdot \log \frac{D_{12}}{d_{12}} = 2 \times 10^{- 4} \log \frac{\sqrt{16^{2} + 1}}{1} = 0.5549 \times 10^{- 3} H / км \\ L = [\begin{matrix} L_{11} & L_{12} \\ L_{21} & L_{22} \end{matrix}] = [\begin{matrix} 1.583 \times 10^{- 3} & 0.5549 \times 10^{- 3} \\ 0.5549 \times 10^{- 3} & 1.583 \times 10^{- 3} \end{matrix}] H / км \end{matrix}$

Само - и взаимные емкости вычисляются можно следующим образом:

$\begin{matrix} P_{11} = P_{22} = \frac{1}{2 π ε_{o}} \log \frac{2 h}{r_{i}} = 1.7975 \times 10^{7} \log \frac{2 \times 8}{0.75 \times 10^{- 2}} = 1.3779 \times 10^{8} км / F \\ P_{12} = P_{21} = \frac{1}{2 π ε_{o}} \log \frac{D_{12}}{d_{12}} = 1.7975 \times 10^{7} \log \frac{\sqrt{16^{2} + 1}}{1} = 4.9872 \times 10^{7} км / F \\ C = {[\begin{matrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{matrix}]}^{- 1} = [\begin{matrix} 8.352 \times 10^{- 9} & - 3.023 \times 10^{- 9} \\ - 3.023 \times 10^{- 9} & 8.352 \times 10^{- 9} \end{matrix}] F / км \end{matrix}$

Вы сначала создаете шаблон LDATA структура, чтобы задать геометрию линии и тип проводников этой линии. В подсказке MATLAB^® введите:

LDATA = power_lineparam('new');

Затем установите следующие поля с определенными значениями:

 LDATA.frequency = 50;
 LDATA.groundResistivity = 0;
 LDATA.Geometry.NPhaseBundle = 2;
 LDATA.Geometry.NGroundBundle = 0;
 LDATA.Geometry.PhaseNumber = [1,2];
 LDATA.Geometry.X = [0,1];
 LDATA.Geometry.Ytower = [8,8];
 LDATA.Geometry.Ymin = [8,8];
 LDATA.Geometry.ConductorType = [1,1];
 % define conductor Type 1:
 LDATA.Conductors.Diameter = [1.5];
 LDATA.Conductors.ThickRatio = [0.5];
 LDATA.Conductors.GMR = [0.5841];
 LDATA.Conductors.Res = [0.1601];
 LDATA.Conductors.Mur = [1];
 LDATA.Conductors.Nconductors = [1];
 LDATA.Conductors.BundleDiameter =[0];
 LDATA.Conductors.AngleConductor1 = [0];
 LDATA.Conductors.skinEffect = 'no';

Затем вы вычисляете параметры линии RLC с командой:

 LDATA = power_lineparam(LDATA);
 disp(LDATA.R),disp(LDATA.L),disp(LDATA.C)

Модель PI для 1-километровой линии получена из R, L, и матриц C. PI значения RLC выведен из само - и взаимные условия R, L, и матрицы C. Индексы s и m определяют само - и взаимные условия в R, L, и матрицы C.

R_p1 = R_p2 = R _s = 0,1601 Ω / км

L_p1 = L_p2 = L _s = 1,583 мГн/км

C_p1 = C_p2 = C _s + C _m = 8.352 – 3.023 = 5,329 нФ/км (2,664 нФ в каждом конце раздела PI)

C_p1p2 = – C _m = 3,023 нФ/км (1,511 нФ в каждом конце раздела PI)

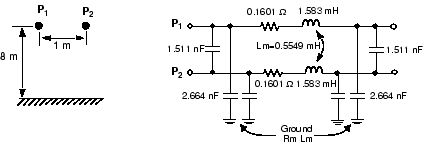
Можно также варьироваться наземное удельное сопротивление и частота, чтобы заметить, что их удар на сопротивление и индуктивность проводника и земли возвращается.

Следующий код варьируется наземное удельное сопротивление от нуля до 10 000 Ω.m:

Rground = [0,10,100,10000]
for k=1:4
   LDATA.groundResitivity = Rground(k);
   LDATA = power_lineparam(LDATA);
   ConductorRS_RM(k) = LDATA.R(1,1)-LDATA.R(1,2);
   GroundRm(k) = LDATA.R(1,2);
   ConductorLs_Lm(k) = LDATA.L(1,1)-LDATA.L(1,2);
   GroundLm(k) = LDATA.L(1,2);
end

Необходимо перечислить значения в следующей таблице. Комната RS выражений и Ls-Lm представляют соответственно сопротивление и индуктивность проводника, тогда как Rm и Lm являются сопротивлением, и индуктивность земли возвращаются.

Удар наземного удельного сопротивления (частота = 50 Гц; эффект кожи, не включенный)

Земля Удельное сопротивление (Ω.m)	Проводник Комната RS (Ω / км)	Земля \rm (Ω / км)	Проводник Ls-Lm (mH/km)	Земля Lm (mH/km)
0	0.1601	0	1.028	0.5549
10	0.1601	0.04666	1.029	1.147
100	0.1601	0.04845	1.029	1.370
10 000	0.1601	0.04925	1.029	1.828

Когда наземное удельное сопротивление варьируется по нормальной области значений (между 10 Ω.m для влажной почвы и 10 000 Ω.m для сухой, скалистой земли), наземное сопротивление остается почти постоянным в 0.05 Ω/km, тогда как его индуктивность увеличивается с 1,15 мГн/км до 1,83 мГн/км.

Используя следующий код, повторите расчет с различными частотами в пределах от от 0,05 Гц до 50 кГц и с проводниковым эффектом кожи, смоделированным для наземного удельного сопротивления 100 Ом-m.

LDATA.groundResitivity = 100;
Frequencies = [0.05,50,500,5000,50000]
for k=1:5
   LDATA.frequency = Frequencies(k);
   LDATA = power_lineparam(LDATA);
   ConductorRS_RM(k) = LDATA.R(1,1)-LDATA.R(1,2);
   GroundRm(k) = LDATA.R(1,2);
   ConductorLs_Lm(k) = LDATA.L(1,1)-LDATA.L(1,2);
   GroundLm(k) = LDATA.L(1,2);
end

Удар частоты (наземное удельное сопротивление = 100 Ω.m; с проводниковым эффектом кожи)

Частота (Гц)	Проводник Комната RS (Ω / км)	Земля \rm (Ω / км)	Проводник Ls-Lm (mH/km)	Земля Lm (mH/km)
0.05	0.1601	4.93e-5	1.029	2.058
50	0.1606	0.04844	1.029	1.370
500	0.2012	0.4666	1.022	1.147
5000	0.5442	4.198	0.9944	0.9351
50 000	1.641	32.14	0.9836	0.7559

Эта таблица показывает, что частота оказывает очень большое влияние на наземное сопротивление, но намного более низкое влияние на наземную индуктивность. Из-за эффекта кожи в земле, когда частота увеличивается, блуждающий ток течет ближе на поверхность, уменьшая эквивалентный раздел заземляющего проводника и таким образом увеличивая его сопротивление. Когда блуждающий ток перемещается на более низкой глубине на высоких частотах, индуктивность цикла проводника плюс земля возвращают (или самоиндукция, Ls) уменьшения.

Из-за проводникового эффекта кожи частота оказывает значимое влияние на проводниковое сопротивление от нескольких сотен из герц, но незначительный удар на проводниковую индуктивность. На номинальной системной частоте (50 Гц или 60 Гц), увеличение проводникового сопротивления относительно сопротивления DC (0.1601 Ω/km) составляет только 0,3%.

Второй пример соответствует 500 кВ, трехфазная, двухконтурная линия.

Степень передается более чем шесть проводников фазы, формирующих две трехфазных схемы. Линия защищена от молнии двумя заземляющими проводами. Проводники фазы используют пакеты трех подпроводников. Подпроводники расположены во главе равностороннего треугольника сторон на 50 см, соответствуя диаметру пакета на 57,735 см. Эта настройка линии соответствует одной показанной на рисунке Настройке Трехфазной Двухконтурной Линии.

Нумерация фазы собиралась получить параметры линии трехфазной линии, эквивалентной этим двум схемам, соединенным параллельно. В разделе Compute нажмите RLC Line Parameters, чтобы отобразить R, L, и матрицы C и параметры последовательности.

Положительная последовательность и параметры нулевой последовательности транспонированной линии отображены в разделе Computed Parameters в R10 и векторах L10:

R1 = 0,009009 Ω/km R0=0.2556 Ω/km

L1 = L0 на 0,4408 мГн/км = 2,601 мГн/км

C0=11.62 nF/km C1 =25.87 нФ/км

Можно также получить параметры двух отдельных схем и иметь доступ к шести проводникам фазы. Измените количества фазы проводников p4, p5, и p6 (схема 2) к 6, 5, и 4, соответственно. Положительная последовательность, нулевая последовательность и взаимные параметры нулевой последовательности транспонированной линии:

R1 = 0,01840 Ω/km R0 =0.2649 Ω/km R0m = 0.2462 Ω/km

L1 = L0 на 0,9296 мГн/км = фунт на 3,202 мГн/км 0m = 2,0 мГн/км

C1 C0 на =12.57 нФ/км C0m на =7.856 нФ/км = −2.044 nF/km

Когда линия симметрична, положительные - и параметры нулевой последовательности для схемы 2 идентичны параметрам схемы 1.

Ссылки

[1] Dommel, H., и др., Электромагнитный Переходный Справочник Программы (Книга Теории EMTP), 1986.

[2] Карсон, J. R. "Распространение волны в Воздушных проводах с Землей Возвращается", Системы Bell Технический Журнал, Издание 5, стр 539-554, 1926.

Документация

power_lineparam

Синтаксис

Описание

Примеры

Ссылки

Смотрите также

Документация Simscape Electrical

Поддержка