Извилистая машина

Введение

Извилистые машины, также названные лентопротяжными механизмами, используются в целлюлозно-бумажной промышленности, а также в ткани, стали и пластмассовых отраслях промышленности.

Важная характеристика большинства лентопротяжных механизмов - то, что сила, действующая на извилистый материал, должна остаться постоянной. Это понято путем управления крутящим моментом лентопротяжного механизма пропорционально к радиусу переменной списка. Обратите внимание на то, что это принято здесь, что материал питается лентопротяжный механизм на постоянной скорости. Последний подразумевает, что лентопротяжный механизм угловая скорость обеспечен, чтобы уменьшиться пропорционально к радиусу списка. Следовательно извилистая машина является постоянным приложением степени, потому что продукт крутящего момента механического устройства лентопротяжного механизма и его угловой скорости является постоянным.

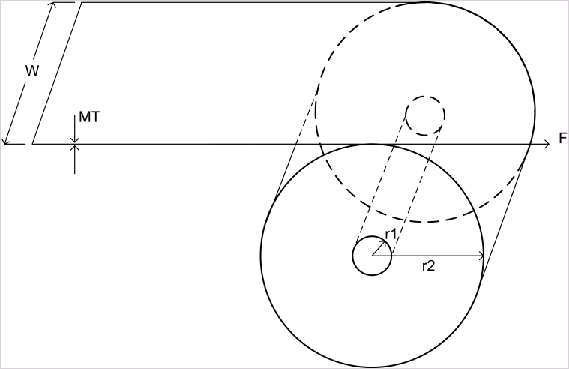
Описание лентопротяжного механизма

Следующие графические показы физическое представление лентопротяжного механизма, где W является шириной списка, _r1базовый радиус, _r2радиус списка и MT толщина материала.

Физическое представление лентопротяжного механизма

Около переменных, описанных выше, симуляция также требует следующих параметров и переменных:

MV	Масса материала на единичный объем
L	Длина материала
M	Масса материала
_Jr	Материальная инерция
_Jc	Инерция ядра лентопротяжного механизма
_Bω	Коэффициент вязкого трения лентопротяжного механизма

Схема полной извилистой системы

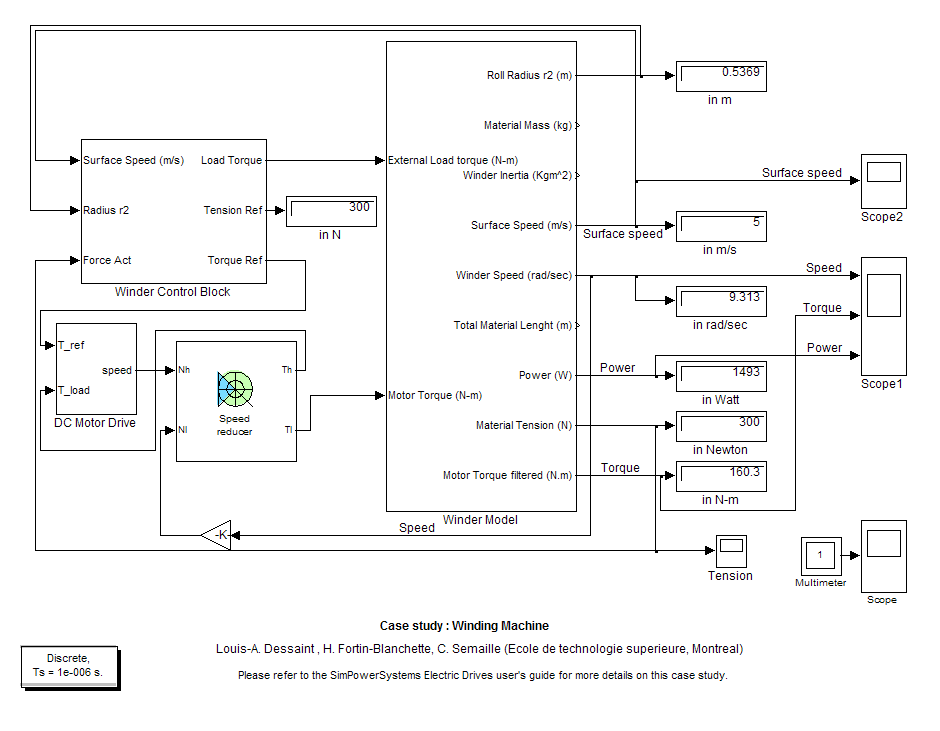
Схема Полной Извилистой Системы показывает схему Simulink^® полной извилистой системы. Эта система состоит из четырех блоков: блок Winder Control, блок DC Motor Drive, блок Speed Reducer и блок Winder Model.

Блокируйте описание

Блок Model лентопротяжного механизма

Этот блок вычисляет различные переменные лентопротяжного механизма с помощью следующих уравнений.

Поверхностная скорость S

$S = ω \cdot r_{2}$

где ω является лентопротяжным механизмом угловая скорость.

Длина материала L

$L = \int S d t$

Прокрутите радиус _r2

$r_{2} = \sqrt{\frac{L \cdot M T}{π} + r_{1}^{2}}$

Материальный массовый M

$M = M V \cdot π \cdot W \cdot (r_{2}^{2} - r_{1}^{2})$

Общая инерция лентопротяжного механизма _Jtи материальная инерция _Jω

$J_{t} = J_{ω} + J_{c}$

где

$J_{ω} = \frac{1}{2} \cdot M \cdot (r_{2}^{2} + r_{1}^{2})$

Лентопротяжный механизм угловая скорость вычисляется с помощью следующего дифференциального уравнения

$T_{e} = J_{t} \frac{d ω}{d t} + B \cdot ω + T_{l}$

где _Tlявляется крутящим моментом нагрузки лентопротяжного механизма, и _Teявляется электроприводом электрический крутящий момент. Вычисление силы или силы, F, примененный на извилистый материал, основан на том же дифференциальном уравнении как выше, где крутящий момент нагрузки описывается как _Tl = F · _{r2 .} Реорганизация уравнений с точки зрения выражений F

$F = \frac{T_{e} - (J_{t} \cdot \dot{ω}) - (B \cdot ω)}{r_{2}}$

Эта предполагаемая сила возвращена с блоком Winder Control для того, чтобы быть отрегулированной.

Обратите внимание на то, что в вышеупомянутых двух уравнениях, термине $ω \cdot {\dot{J}}_{t}$ не использован, потому что это, как находили, было незначительно для случая, рассмотренного здесь.

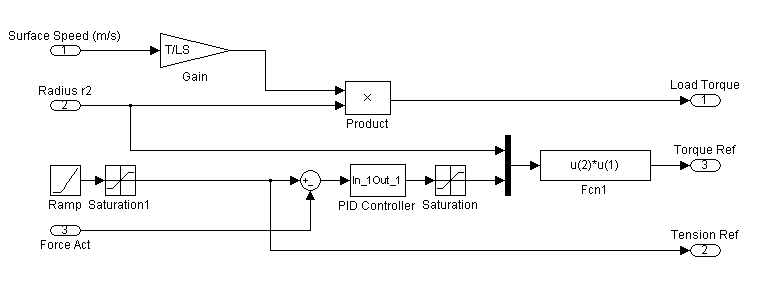
Блок управления лентопротяжного механизма

Этот блок содержит ПИД-регулятор, который регулирует силу, примененную на извилистый материал. Выход этого контроллера силы является точкой множества элементарных исходов крутящего момента для электропривода лентопротяжного механизма. Блок Winder Control, показанный в Блоке управления Лентопротяжного механизма также, содержит силу по сравнению с характеристикой скорости внешнего процесса, предоставляющего материал к лентопротяжному механизму на постоянной скорости. Эта характеристика состоит в прямой линии наклона, равного отношению ссылочной существенной силы на постоянной поверхностной скорости.

Блок управления лентопротяжного механизма

Блок диска двигателя постоянного тока

Этот блок содержит полный 2D квадрантный диск DC трехфазного выпрямителя со своим трехфазным источником напряжения. Диск DC оценивается 5 л. с., 220 В, 50 Гц и является отрегулированным крутящим моментом.

Блок редуктора скорости

Двигатель постоянного тока соединяется с лентопротяжным механизмом блоком Speed Reducer. Отношение сокращения скорости равняется 10, позволяя лентопротяжному механизму стать в 10 раз медленнее, чем двигатель, в то время как переданный валом крутящий момент почти в 10 раз выше на низкоскоростной стороне. Крутящий момент, требуемый лентопротяжным механизмом в этом тематическом исследовании, является приблизительно 200 N.m.

Результаты симуляции

Извилистая имитационная модель машины содержится в файле cs_winder. Параметры симуляции являются теми из статьи извилистое приложение, где ширина списка составляет 10 м. Откройте файл и посмотрите на параметры в масках Simulink блока Winder Model, блока Winder Control, блока DC Motor Drive и блока Speed Reducer. В блоке Winder Control вы будете видеть, что сетбол силы составляет 300 Н, и поверхностный сетбол скорости составляет 5 м/с.

Скорость изменения сетбола силы ограничивается внутренне 25 Н/с так, чтобы сетбол силы потребовал, чтобы 12 с достигли его окончательного значения. Обратите внимание на то, что шаг времени симуляции полной модели составляет 1 мкс для того, чтобы выполнить редуктор скорости, который является блоком, который требует самого маленького шага времени симуляции.

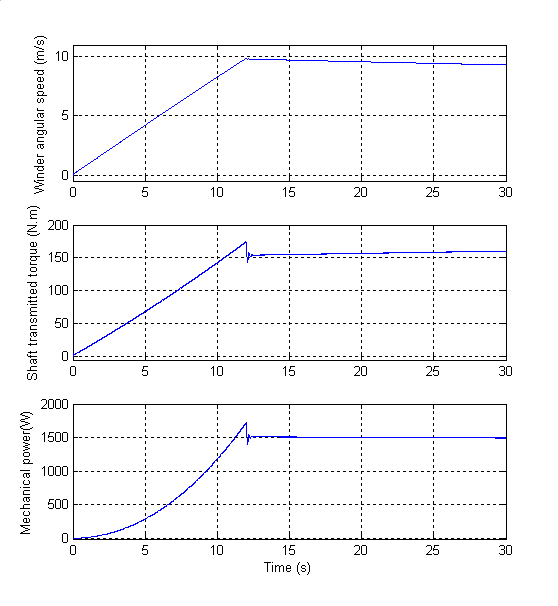
Запустите симуляцию и наблюдайте, как хорошо существенная сила и поверхностная скорость сползают к их заданным значениям в Существенной Силе и Поверхностной Скорости соответственно. Лентопротяжный механизм Угловая Скорость, Механический Крутящий момент и Степень показывает лентопротяжному механизму угловую скорость, механический крутящий момент и степень. Обратите внимание на то, что, если рабочая точка достигнута (300 Н, 5 м/с), угловые уменьшения скорости и увеличения крутящего момента, оба линейно, так, чтобы степень была приблизительно постоянной. Причина, почему механическая энергия не является точно постоянной, но уменьшения немного, состоит в том, что уменьшающийся лентопротяжный механизм скорости собственная инерция предоставляет небольшую часть постоянной степени, требуемой лентопротяжным механизмом.

Существенная сила

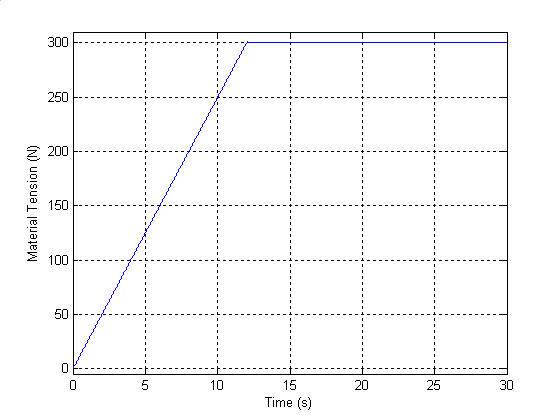
Поверхностная скорость

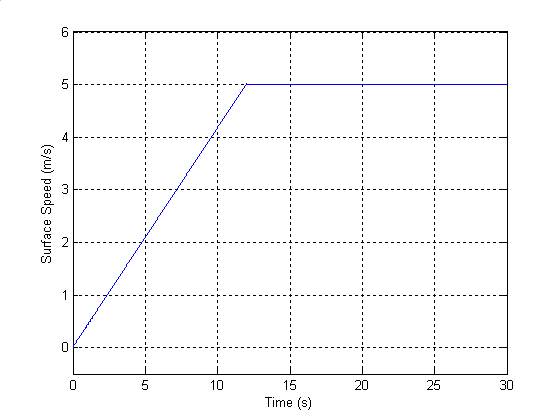
Лентопротяжный механизм угловая скорость, механический крутящий момент и степень

Документация