Считайте многомерную систему управления с обратной связью показанной в следующем рисунке. Для того, чтобы определить количество многомерных запасов устойчивости и эффективности таких систем, можно использовать сингулярные значения матриц передаточной функции с обратной связью от r до каждых из этих трех выходных параметров e, u, и y, то есть.
где L (s) является матрицей передаточной функции цикла
| (1) |
Блок-схема многомерной системы управления с обратной связью

Эти две матрицы S (s) и T (s) известны как функцию чувствительности и дополнительную функцию чувствительности, соответственно. Матричный R (s) не имеет никакого общего названия. Диаграммы Боде сингулярного значения каждой из трех матриц передаточной функции S (s), R (s) и T (s) играют важную роль в устойчивом многомерном проекте системы управления. Сингулярные значения матрицы передаточной функции цикла, L (s) важен, потому что L (s) определяет матрицы S (s) и T (s).
Сингулярные значения S (j ω) определяют затухание воздействия, потому что S (s) является на самом деле передаточной функцией с обратной связью от воздействия, d, чтобы посадить выход y — видит Блок-схему Многомерной Системы Управления с обратной связью. Таким образом требования по производительности затухания воздействия могут быть записаны как
| (2) |
где желаемый фактор затухания воздействия. Разрешение чтобы зависеть от частоты, ω позволяет вам задать различный фактор затухания для каждой частоты ω.
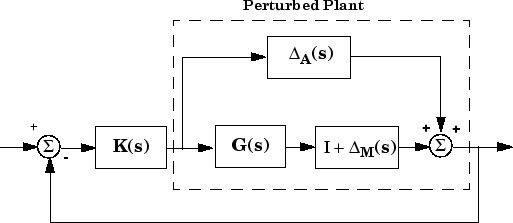
Диаграммы Боде сингулярного значения R (s) и T (s) используются, чтобы измерить запасы устойчивости многомерных проектов обратной связи перед лицом аддитивных возмущений объекта ΔA и мультипликативные возмущения объекта ΔM, соответственно. Смотрите следующую фигуру.
Рассмотрите, как Диаграмма Боде сингулярного значения дополнительной чувствительности T (s) определяет запас устойчивости для мультипликативных возмущений ΔM. Мультипликативный запас устойчивости является, по определению, "размером" самого маленького устойчивого ΔM (s), который дестабилизирует систему на рисунке ниже когда ΔA = 0.
Аддитивная/Мультипликативная Неопределенность
Взятие чтобы быть определением "размера" ΔM (jω), у вас есть следующая полезная характеристика "мультипликативной" робастности устойчивости:
Мультипликативная робастность:
Размер наименьшей дестабилизирующей мультипликативной неопределенности ΔM (s):
Меньшее , чем больше будет размер самого маленького дестабилизирующего мультипликативного возмущения, и следовательно, тем больше будет запас устойчивости.
Подобный результат доступен для связи запаса устойчивости перед лицом аддитивных возмущений объекта ΔA (s) к R (s), если вы берете быть определением "размера" ΔA (jω) на частоте ω.
Аддитивная робастность:
Размер наименьшей дестабилизирующей аддитивной неопределенности ΔA:
В результате теорем робастности 1 и 2, распространено задать запасы устойчивости систем управления через неравенства сингулярного значения такой как
| (3) |
| (4) |
где |W2 (jω) | и |W3 (jω) | являются соответствующими размерами крупнейших ожидаемых аддитивных и мультипликативных возмущений объекта.
Это - установившаяся практика, чтобы смешать эффекты всей неопределенности объекта в одно фиктивное мультипликативное возмущение ΔM, так, чтобы требования системы управления могли быть записаны
как показано в Технических требованиях Сингулярного значения на L, S, и T.
Интересно отметить это в верхней половине фигуры (выше линии на 0 дБ),
в то время как в более низкой половине Технических требований Сингулярного значения на L, S, и T (ниже линии на 0 дБ),
Это следует из факта это
если , и
если .
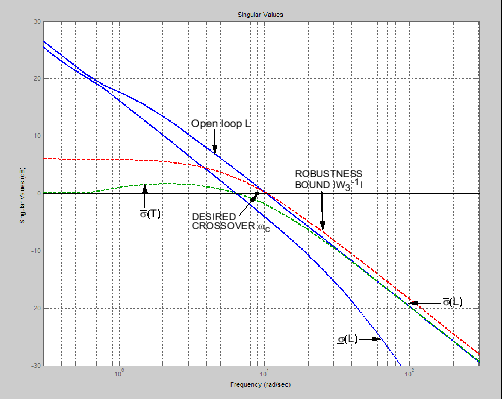
Технические требования сингулярного значения на L, S, и T
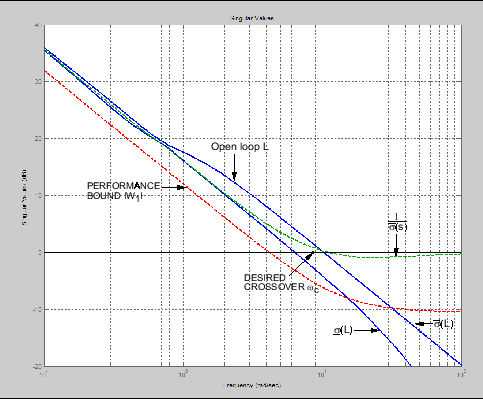
Таким образом весьма распространено видеть технические требования на затухании воздействия и мультипликативном запасе устойчивости, описанном непосредственно в терминах запретных областей для Диаграмм Боде σi (L (jω)) как "цикл сингулярного значения, формирующий" требования, или как заданные верхние / нижние границы или когда цель желала, чтобы форма цикла — видела предыдущую фигуру.
Для тех, кто более доволен классическими одноконтурными концепциями, существуют важные связи между мультипликативными запасами устойчивости, предсказанными и предсказанные классическими M-кругами, как найдено на графике Николса. Действительно в single-input/single-output случае,
который является точно количеством, вы получаете из M-кругов графика Николса. Таким образом, многоконтурное обобщение резонансной пиковой величины с обратной связью, которая, как классические эксперты по управлению распознают, тесно связана с коэффициентом затухания доминирующих полюсов с обратной связью. Кроме того, оказывается, что можно иметь отношение , к классическому запасу по амплитуде GM и запас по фазе θM в каждой обратной связи многомерной системы с обратной связью Блок-схемы Многомерной Системы Управления с обратной связью через формулы:
(См. [6].) Эти формулы допустимы обеспеченный и больше, чем 1, когда обычно имеет место. Поля применяются, даже когда возмущения усиления или возмущения фазы происходят одновременно в нескольких каналах обратной связи.
Нормы по бесконечности S и T также дают к допускам сокращения усиления. Допуск сокращения усиления gm задан, чтобы быть минимальной суммой, которой должны были бы быть уменьшены усиления в каждом цикле для того, чтобы дестабилизировать систему. Верхние границы на gm следующие:
Команда loopsyn позволяет вам спроектировать стабилизировавшийся контроллер обратной связи, чтобы оптимально сформировать частотную характеристику разомкнутого контура системы управления с обратной связью MIMO, чтобы соответствовать максимально тесно, желаемый цикл формирует Gd. Базовый синтаксис loopsyn формирующая цикл команда синтеза контроллера:
K = loopsyn(G,Gd)
Здесь G матрица передаточной функции LTI модели объекта управления MIMO, Gd желаемая форма цикла цели для передаточной функции цикла L=G*K, и K оптимальный формирующий цикл контроллер. Контроллер LTI K имеет свойство, что оно формирует цикл L=G*K так, чтобы это совпадало с частотной характеристикой Gd максимально тесно согласно ограничению, что компенсатор должен стабилизировать модель объекта управления G.