Иерархические данные групп кластеризации по множеству шкал путем создания кластерного дерева или dendrogram. Дерево не является ни одним набором кластеров, а скорее многоуровневой иерархией, где к кластерам на одном уровне соединяют как кластеры на следующем уровне. Это позволяет вам решать уровень или шкалу кластеризации, которая наиболее подходит для вашего приложения. Функция clusterdata поддерживает агломерационную кластеризацию и выполняет все необходимые шаги для вас. Это соединяется pdist, linkage, и cluster функции, которые можно использовать отдельно для более детального анализа. dendrogram графики функций кластерное дерево.
Чтобы выполнить агломерационный иерархический кластерный анализ набора данных с помощью функций Statistics and Machine Learning Toolbox™, выполните эту процедуру:
Найдите подобие или несходство между каждой парой объектов в наборе данных. На этом шаге вы вычисляете расстояние между объектами с помощью pdist функция. pdist функционируйте поддерживает много различных способов вычислить это измерение. Смотрите Меры по Подобию для получения дополнительной информации.
Сгруппируйте объекты в двоичный файл, иерархическое кластерное дерево. На этом шаге вы соединяете пары объектов, которые находятся в непосредственной близости с помощью linkage функция. linkage функционируйте использует информацию о расстоянии, сгенерированную на шаге 1, чтобы определить близость объектов друг другу. Когда объекты соединяются в бинарные кластеры, недавно сформированные кластеры сгруппированы в большие кластеры, пока иерархическое дерево не формируется. Смотрите Рычажные устройства для получения дополнительной информации.
Определите, где сократить иерархическое дерево в кластеры. На этом шаге вы используете cluster функционируйте, чтобы сократить, отклоняется нижняя часть иерархического дерева, и присвойте все объекты ниже каждого сокращения к одному кластеру. Это создает раздел данных. cluster функция может создать эти кластеры путем обнаружения естественных группировок в иерархическом дереве или путем отключения иерархического дерева в произвольной точке.
Следующие разделы предоставляют больше информации о каждом из этих шагов.
Примечание
Функция clusterdata выполняет все необходимые шаги для вас. Вы не должны выполняться pdist, linkage, или cluster функции отдельно.
Вы используете pdist функция, чтобы вычислить расстояние между каждой парой объектов в наборе данных. Для набора данных, составленного из объектов m, существует m* (m – 1)/2 пары в наборе данных. Результат этого расчета обычно известен как матрицу несходства или расстояние.
Существует много способов вычислить эту информацию о расстоянии. По умолчанию, pdist функция вычисляет Евклидово расстояние между объектами; однако, можно задать одну из нескольких других опций. Смотрите pdist для получения дополнительной информации.
Примечание
Можно опционально нормировать значения в наборе данных прежде, чем вычислить информацию о расстоянии. В наборе данных реального мира переменные могут быть измерены против различных шкал. Например, одна переменная может измерить экзаменационные отметки Коэффициента умственного развития (IQ), и другая переменная может измерить окружность головы. Эти несоответствия могут исказить вычисления близости. Используя zscore функция, можно преобразовать все значения в наборе данных, чтобы использовать ту же пропорциональную шкалу. Смотрите zscore для получения дополнительной информации.
Например, рассмотрите набор данных, X, составленный из пяти объектов, где каждый объект является набором x, y координаты.
Объект 1: 1, 2
Объект 2: 2.5, 4.5
Объект 3: 2, 2
Объект 4: 4, 1.5
Объект 5: 4, 2.5
Можно задать этот набор данных как матрицу
rng default; % For reproducibility X = [1 2;2.5 4.5;2 2;4 1.5;... 4 2.5];
и передайте его pdist. pdist функция вычисляет расстояние между объектом 1 и объектом 2, объект 1 и объект 3, и так далее пока расстояния между всеми парами не были вычислены. Следующая фигура строит эти объекты в графике. Евклидово расстояние между объектом 2 и объектом 3, как показывают, иллюстрирует одну интерпретацию расстояния.
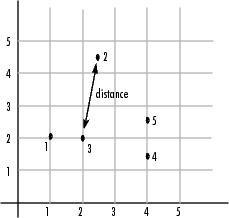
pdist функция возвращает эту информацию о расстоянии в векторе, Y, где каждый элемент содержит расстояние между парой объектов.
Y = pdist(X)
Y = 1×10
2.9155 1.0000 3.0414 3.0414 2.5495 3.3541 2.5000 2.0616 2.0616 1.0000
Облегчить видеть отношение между информацией о расстоянии, сгенерированной pdist и объекты в исходном наборе данных, можно переформатировать вектор расстояния в матрицу с помощью squareform функция. В этой матрице элемент i, j соответствует расстоянию между объектом i и объектом j в исходном наборе данных. В следующем примере элемент 1,1 представляет расстояние между объектом 1 и им (который является нулем). Элемент 1,2 представляет расстояние между объектом 1 и объектом 2 и так далее.
squareform(Y)
ans = 5×5
0 2.9155 1.0000 3.0414 3.0414
2.9155 0 2.5495 3.3541 2.5000
1.0000 2.5495 0 2.0616 2.0616
3.0414 3.3541 2.0616 0 1.0000
3.0414 2.5000 2.0616 1.0000 0
Если близость между объектами в наборе данных была вычислена, можно определить, как объекты в наборе данных должны быть сгруппированы в кластеры, с помощью linkage функция. linkage функционируйте берет информацию о расстоянии, сгенерированную pdist и пары ссылок объектов, которые являются близко друг к другу в бинарные кластеры (кластеры, составленные из двух объектов). linkage функционируйте затем соединяет эти недавно сформированные кластеры друг с другом и с другими объектами создать большие кластеры, пока все объекты в исходном наборе данных не соединены в иерархическом дереве.
Например, учитывая вектор расстояния Y сгенерированный pdist от множества x выборочных данных и y-координат, linkage функция генерирует иерархическое кластерное дерево, возвращая информацию о рычажном устройстве в матрице, Z.
Z = linkage(Y)
Z = 4×3
4.0000 5.0000 1.0000
1.0000 3.0000 1.0000
6.0000 7.0000 2.0616
2.0000 8.0000 2.5000
В этом выходе каждая строка идентифицирует ссылку между объектами или кластерами. Первые два столбца идентифицируют объекты, которые были соединены. Третий столбец содержит расстояние между этими объектами. Для множества x выборочных данных и y-координат, linkage функция начинается группировками объектов 4 и 5, которые имеют самую близкую близость (значение расстояния = 1.0000). linkage функция продолжается группировками объектов 1 и 3, которые также имеют значение расстояния 1,0000.
Третья строка указывает что linkage функциональные сгруппированные объекты 6 и 7. Если исходный набор выборочных данных содержал только пять объектов, что такое объекты 6 и 7? Объект 6 является недавно сформированным бинарным кластером, созданным группировкой объектов 4 и 5. Когда linkage функциональные группы два объекта в новый кластер, это должно присвоить кластер значение уникального индекса, начиная со значения m + 1, где m является количеством объектов в исходном наборе данных. (Значения 1 через m уже используются исходным набором данных.) Точно так же возражают 7, кластер, сформированный группировками объектов 1 и 3.
linkage расстояния использования, чтобы определить порядок, в котором это кластеризирует объекты. Вектор расстояния Y содержит расстояния между исходными объектами 1 - 5. Но рычажное устройство должно также смочь определить расстояния включающие кластеры, которые оно создает, такие как объекты 6 и 7. По умолчанию, linkage использует метод, известный как одно рычажное устройство. Однако существует много различных доступных методов. Смотрите linkage страница с описанием для получения дополнительной информации.
Как итоговый кластер, linkage функциональный сгруппированный объект 8, недавно сформированный кластер, составленный из объектов 6 и 7, с объектом 2 от исходного набора данных. Следующая фигура графически иллюстрирует путь linkage группирует объекты в иерархию кластеров.
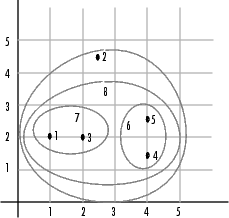
Иерархическое, бинарное кластерное дерево создается linkage функция является самой понятной, когда просматривается графически. Функция dendrogram строит дерево можно следующим образом.
dendrogram(Z)

На рисунке числа вдоль горизонтальной оси представляют индексы объектов в исходном наборе данных. Ссылки между объектами представлены как вверх тормашками U-образные линии. Высота U указывает на расстояние между объектами. Например, ссылка, представляющая кластер, содержащий, возражает 1, и 3 имеет высоту 1. Ссылка, представляющая кластер, которому группы возражают 2 вместе с объектами 1, 3, 4, и 5, (которые уже кластеризируются как объект 8), имеет высоту 2,5. Высота представляет расстояние linkage вычисляет между объектами 2 и 8. Для получения дополнительной информации о создании схемы древовидной схемы, смотрите dendrogram страница с описанием.
После соединения объектов в наборе данных в иерархическое кластерное дерево вы можете хотеть проверить что расстояния (то есть, высоты) в древовидном отражении исходные расстояния точно. Кроме того, вы можете хотеть исследовать естественные деления, которые существуют среди ссылок между объектами. Функции Statistics and Machine Learning Toolbox доступны для обеих из этих задач, как описано в следующих разделах.
В иерархическом кластерном дереве любые два объекта в исходном наборе данных в конечном счете соединены на некотором уровне. Высота ссылки представляет расстояние между двумя кластерами, которые содержат те два объекта. Эта высота известна как cophenetic расстояние между двумя объектами. Один способ измериться, как хорошо кластерное дерево, сгенерированное linkage функция отражает, что ваши данные должны сравнить cophenetic расстояния с исходными данными о расстоянии, сгенерированными pdist функция. Если кластеризация допустима, соединение объектов в кластерном дереве должно иметь сильную корреляцию с расстояниями между объектами на расстоянии вектор. cophenet функция сравнивает эти два множества значений и вычисляет их корреляцию, возвращение значения вызвало cophenetic коэффициент корреляции. Чем ближе значение cophenetic коэффициента корреляции к 1, тем более точно решение по кластеризации отражает ваши данные.
Можно использовать cophenetic коэффициент корреляции, чтобы сравнить результаты кластеризации того же набора данных с помощью различных методов расчета расстояния или кластеризируя алгоритмы. Например, можно использовать cophenet функция, чтобы оценить кластеры, созданные для набора выборочных данных.
c = cophenet(Z,Y)
c = 0.8615
Z матрица, выведенная linkage функция и Y вектор расстояния, выведенный pdist функция.
Выполните pdist снова на том же наборе данных, на этот раз задавая метрику городского квартала. После выполнения linkage функция на этом новом pdist выведите использование среднего метода рычажного устройства, вызовите cophenet оценивать решение по кластеризации.
Y = pdist(X,'cityblock'); Z = linkage(Y,'average'); c = cophenet(Z,Y)
c = 0.9047
cophenetic коэффициент корреляции показывает, что использование различного расстояния и метода рычажного устройства создает дерево, которое представляет исходные расстояния немного лучше.
Один способ определить естественные кластерные деления в наборе данных состоит в том, чтобы сравнить высоту каждой ссылки в кластерном дереве с высотами соседних ссылок ниже это в дереве.
Ссылка, которая является приблизительно той же высотой как ссылки ниже, это указывает, что нет никаких отличных делений между объектами, к которым соединяют на этом уровне иерархии. Эти ссылки, как говорят, показывают высокий уровень непротиворечивости, потому что расстояние между объектами, к которым соединяют, является приблизительно тем же самым как расстояниями между объектами, которые они содержат.
С другой стороны, ссылка, высота которой отличается заметно от высоты ссылок ниже, это указывает, что объекты, к которым соединяют на этом уровне в кластерном дереве, намного более далеки друг кроме друга, чем их компоненты, состояла в том, когда к ним соединили. Эта ссылка, как говорят, противоречива со ссылками ниже он.
В кластерном анализе противоречивые ссылки могут указать на границу естественного деления в наборе данных. cluster функционируйте использует количественные показатели несоответствия, чтобы определить, где разделить ваш набор данных в кластеры.
Следующая древовидная схема иллюстрирует противоречивые ссылки. Отметьте, как объекты в древовидной схеме попадают в две группы, которые соединяются ссылками в намного более высоком уровне в дереве. Эти ссылки противоречивы при сравнении со ссылками ниже их в иерархии.
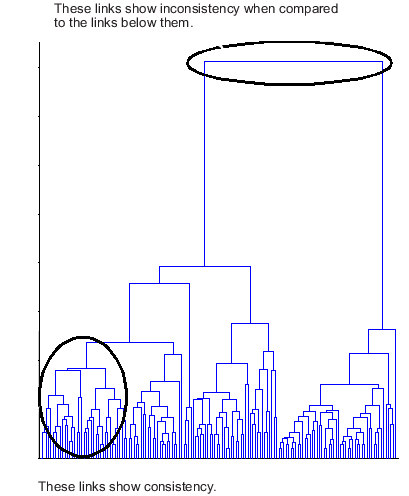
Относительная непротиворечивость каждой ссылки в иерархическом кластерном дереве может быть определена количественно и описана как коэффициент несоответствия. Это значение сравнивает высоту ссылки в кластерной иерархии со средней высотой ссылок ниже это. Ссылки, которые соединяют отличные кластеры, имеют высокий коэффициент несоответствия; ссылки, которые соединяют неясные кластеры, имеют низкий коэффициент несоответствия.
Чтобы сгенерировать список коэффициента несоответствия для каждой ссылки в кластерном дереве, используйте inconsistent функция. По умолчанию, inconsistent функция сравнивает каждую ссылку в кластерной иерархии со смежными ссылками, которые меньше двух уровней ниже его в кластерной иерархии. Это называется глубиной сравнения. Можно также задать другие глубины. Объекты в нижней части кластерного дерева, названного вершинами, которые не имеют никаких дальнейших объектов ниже их, имеют коэффициент несоответствия нуля. Кластеры, которые соединяют два листа также, имеют нулевой коэффициент несоответствия.
Например, можно использовать inconsistent функция, чтобы вычислить значения несоответствия для ссылок, созданных linkage функция в Рычажных устройствах.
Во-первых, повторно вычислите расстояние и значения рычажного устройства с помощью настроек по умолчанию.
Y = pdist(X); Z = linkage(Y);
Затем используйте inconsistent вычислить значения несоответствия.
I = inconsistent(Z)
I = 4×4
1.0000 0 1.0000 0
1.0000 0 1.0000 0
1.3539 0.6129 3.0000 1.1547
2.2808 0.3100 2.0000 0.7071
inconsistent функция возвращает данные о ссылках в (m-1)-by-4 матрица, столбцы которой описаны в следующей таблице.
| Столбец | Описание |
|---|---|
1 | Среднее значение высот всех ссылок включено в вычисление |
2 | Стандартное отклонение всех ссылок включено в вычисление |
3 | Количество ссылок включено в вычисление |
4 | Коэффициент несоответствия |
В демонстрационном выходе первая строка представляет ссылку между объектами 4 и 5. Этот кластер присвоен индекс 6 linkage функция. Поскольку и 4 и 5 вершины, коэффициент несоответствия для кластера является нулем. Вторая строка представляет ссылку между объектами 1 и 3, оба из которых являются также вершинами. Этот кластер присвоен индекс 7 функцией рычажного устройства.
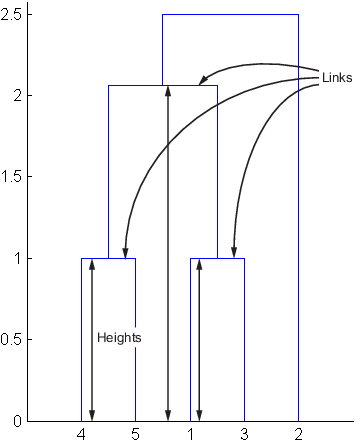
Третья строка оценивает ссылку, которая соединяет эти два кластера, объекты 6 и 7. (Этот новый кластер является присвоенным индексом 8 в linkage вывод . Столбец 3 указывает, что три ссылки рассматриваются в вычислении: сама ссылка и две ссылки непосредственно ниже его в иерархии. Столбец 1 представляет среднее значение высот этих ссылок. inconsistent функционируйте использует вывод информации высоты linkage функция, чтобы вычислить среднее значение. Столбец 2 представляет стандартное отклонение между ссылками. Последний столбец содержит значение несоответствия для этих ссылок, 1.1547. Вот в чем разница между текущей высотой ссылки и средним значением, нормированным на стандартное отклонение.
(2.0616 - 1.3539) / .6129
ans = 1.1547
Следующая фигура иллюстрирует ссылки и высоты, включенные в это вычисление.
Примечание
На предыдущем рисунке нижний предел на оси Y установлен в 0 показать высоты ссылок. Установить нижний предел на 0, выберите Axes Properties в меню Edit кликните по вкладке Y Axis и введите 0 в поле сразу справа от Y Limits.
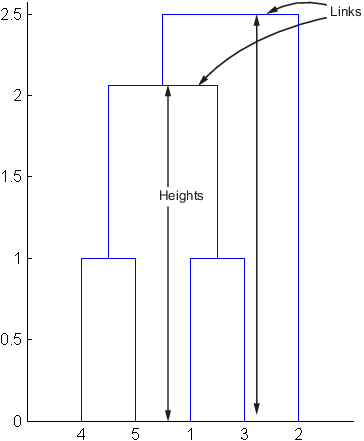
Строка 4 в выходной матрице описывает ссылку между объектом 8 и объектом 2. Столбец 3 указывает, что две ссылки включены в это вычисление: сама ссылка и ссылка непосредственно ниже его в иерархии. Коэффициент несоответствия для этой ссылки 0.7071.
Следующая фигура иллюстрирует ссылки и высоты, включенные в это вычисление.
После того, как вы создадите иерархическое дерево бинарных кластеров, можно сократить дерево, чтобы разделить данные в кластеры с помощью cluster функция. cluster функция позволяет вам создать кластеры двумя способами, как обсуждено в следующих разделах:
Иерархическое кластерное дерево может естественно разделить данные на отличные, хорошо разделенные кластеры. Это может быть особенно очевидно в схеме древовидной схемы, созданной из данных, где группы объектов плотно упаковываются в определенных областях а не в других. Коэффициент несоответствия ссылок в кластерном дереве может идентифицировать эти деления, где общие черты между объектами изменяются резко. (См., Проверяют Кластерное Дерево для получения дополнительной информации о коэффициенте несоответствия.) Можно использовать это значение, чтобы определить где cluster функция создает кластерные контуры.
Например, если вы используете cluster функционируйте, чтобы сгруппировать набор выборочных данных в кластеры, задавая содействующий порог несоответствия 1.2 как значение cutoff аргумент, cluster функциональные группы все объекты в выборочных данных установлены в один кластер. В этом случае ни одна из ссылок в кластерной иерархии не имела коэффициент несоответствия, больше, чем 1.2.
T = cluster(Z,'cutoff',1.2)T = 5×1
1
1
1
1
1
cluster функционируйте выводит вектор, T, это одного размера с исходным набором данных. Каждый элемент в этом векторе содержит количество кластера, в который был помещен соответствующий объект от исходного набора данных.
Если вы понижаете содействующий порог несоответствия к 0.8, cluster функция делит набор выборочных данных на три отдельных кластера.
T = cluster(Z,'cutoff',0.8)T = 5×1
3
2
3
1
1
Этот выход указывает, что возражает 1, и 3 находятся в одном кластере, объекты 4 и 5 находятся в другом кластере и возражают 2, находится в его собственном кластере.
Когда кластеры формируются таким образом, значение сокращения применяется к коэффициенту несоответствия. Эти кластеры, но делают не обязательно, может соответствовать горизонтальному срезу через древовидную схему на определенной высоте. Если вы хотите кластеры, соответствующие горизонтальному срезу древовидной схемы, можно или использовать criterion опция, чтобы указать, что сокращение должно быть основано на расстоянии, а не несоответствии, или можно задать количество кластеров непосредственно как описано в следующем разделе.
Вместо того, чтобы позволить cluster функция создает кластеры, определенные естественными делениями в наборе данных, можно задать количество кластеров, которые вы хотите созданный.
Например, можно указать, что вы хотите cluster функционируйте, чтобы разделить набор выборочных данных в два кластера. В этом случае, cluster функция создает один кластер, содержащий объекты 1, 3, 4, и 5 и другой кластер, содержащий объект 2.
T = cluster(Z,'maxclust',2)T = 5×1
2
1
2
2
2
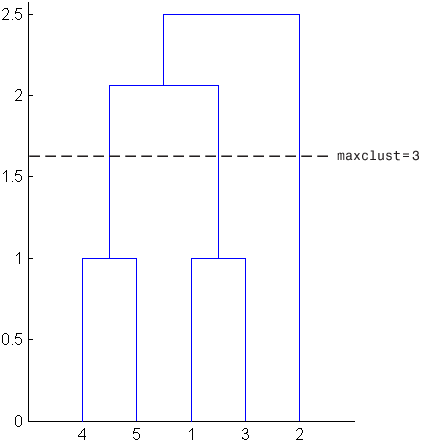
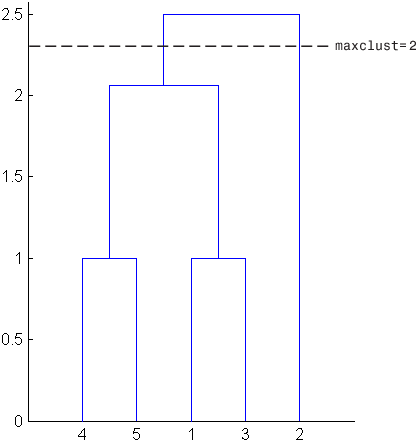
Помочь вам визуализировать как cluster функция определяет эти кластеры, следующий рисунок показывает древовидную схему иерархического кластерного дерева. Горизонтальная пунктирная линия пересекает две линии древовидной схемы, соответствуя установке 'maxclust' к 2. Эти две линии делят объекты в два кластера: объекты ниже левой линии, а именно, 1, 3, 4, и 5, принадлежат одному кластеру, в то время как объект ниже правой линии, а именно, 2, принадлежит другому кластеру.
С другой стороны, если вы устанавливаете 'maxclust' к 3, кластерные функциональные группы возражают 4 и 5 в одном кластере, возражают 1 и 3 во втором кластере и объекте 2 в третьем кластере. Следующая команда иллюстрирует это.
T = cluster(Z,'maxclust',3)T = 5×1
2
3
2
1
1
На этот раз, cluster функция отключает иерархию в более низкой точке, соответствуя горизонтальной линии, которая пересекает три линии древовидной схемы в следующем рисунке.