Интегрирование

Если f символьное выражение, затем

int(f)

попытки найти другое символьное выражение, F, так, чтобы diff(F) = f. Таким образом, int(f) возвращает неопределенный интеграл или антипроизводную f (если каждый существует в закрытой форме). Подобно дифференцированию,

int(f,v)

использует символьный объект v когда переменная интегрирования, а не переменная определяется symvar. Смотрите как int работает путем рассмотрения этой таблицы.

Математическая операция	MATLAB^® Command
$\int x^{n} d x = {\begin{array}{l} \log (x) & если n = - 1 \\ \frac{x^{n + 1}}{n + 1} & в противном случае . \end{array}$	`int(x^n)` или `int(x^n,x)`
$\int_{0}^{π / 2} \sin (2 x) d x = 1$	`int(sin(2x), 0, pi/2)` или `int(sin(2x), x, 0, pi/2)`
g = because(at + b) $\int g (t) d t = \sin (a t + b) / a$	`g = cos(a*t + b) int(g)` или `int(g, t)`
$\int J_{1} (z) d z = - J_{0} (z)$	`int(besselj(1, z))` или `int(besselj(1, z), z)`

В отличие от дифференцирования, символьное интегрирование является более сложной задачей. Много трудностей могут возникнуть в вычислении интеграла:

Антипроизводная, F, может не существовать в закрытой форме.
Антипроизводная может задать незнакомую функцию.
Антипроизводная может существовать, но программное обеспечение не может найти его.
Программное обеспечение могло найти антипроизводную на более крупном компьютере, но заканчивается время или память на доступной машине.

Тем не менее, во многих случаях, MATLAB может выполнить символьное интегрирование успешно. Например, создайте символьные переменные

syms a b theta x y n u z

Следующая таблица иллюстрирует интегрирование выражений, содержащих те переменные.

f	int (f)
syms x n f = x^n;	int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1))
syms y f = y^(-1);	int(f) ans = log(y)
syms x n f = n^x;	int(f) ans = n^x/log(n)
syms a b theta f = sin(a*theta+b);	int(f) ans = -cos(b + a*theta)/a
syms u f = 1/(1+u^2);	int(f) ans = atan(u)
syms x f = exp(-x^2);	int(f) ans = (pi^(1/2)*erf(x))/2

В последнем примере, exp(-x^2), нет никакой формулы для интеграла включающих стандартных выражений исчисления, таких как тригонометрические и показательные функции. В этом случае MATLAB дает ответ в терминах функции ошибок erf.

Если MATLAB не может найти ответ на интеграл функционального f, это только возвращает int(f).

Определенное интегрирование также возможно.

Определенный интеграл	Команда
$\int_{a}^{b} f (x) d x$	`int(f, a, b)`
$\int_{a}^{b} f (v) d v$	`int(f, v, a, b)`

Определенный интеграл

Команда

$\int_{a}^{b} f (x) d x$

int(f, a, b)

$\int_{a}^{b} f (v) d v$

int(f, v, a, b)

Вот некоторые дополнительные примеры.

f	a, B	int (f, a, b)
syms x f = x^7;	a = 0; b = 1;	int(f, a, b) ans = 1/8
syms x f = 1/x;	a = 1; b = 2;	int(f, a, b) ans = log(2)
syms x f = log(x)*sqrt(x);	a = 0; b = 1;	int(f, a, b) ans = -4/9
syms x f = exp(-x^2);	a = 0; b = inf;	int(f, a, b) ans = pi^(1/2)/2
syms z f = besselj(1,z)^2;	a = 0; b = 1;	int(f, a, b) ans = hypergeom([3/2, 3/2],... [2, 5/2, 3], -1)/12

Для Функции Бесселя (besselj) пример, возможно вычислить числовое приближение к значению интеграла, с помощью double функция. Команды

syms z
a = int(besselj(1,z)^2,0,1)

возврат

a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12

и команда

a = double(a)

возвращается

a =
    0.0717

Интеграция с действительными параметрами

Одна из тонкости, вовлеченной в символьное интегрирование, является “значением” различных параметров. Например, если a является каким-либо положительным вещественным числом, выражением

$e^{- a x^{2}}$

положительная, кривая, имеющая форму звонка, которая стремится к 0, как x стремится к ± ∞. Можно создать пример этой кривой для a = 1/2.

syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)

Однако, при попытке вычислить интеграл

$\int_{- \infty}^{\infty} e^{- a x^{2}} d x$

не присваивая значение a, MATLAB принимает, что a представляет комплексное число, и поэтому дает кусочный ответ, который зависит от аргумента a. Если вы только интересуетесь случаем, когда a является положительным вещественным числом, используйте assume установить предположение на a:

syms a
assume(a > 0)

Теперь можно вычислить предыдущий интеграл с помощью команд

syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)

Это возвращается

ans =
pi^(1/2)/a^(1/2)

Интеграция с комплексными параметрами

Вычислить интеграл

$\int_{- \infty}^{\infty} \frac{1}{a^{2} + x^{2}} d x$

для комплексных чисел a, войти

syms a x 
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)

Используйте syms очистить все предположения на переменных. Для получения дополнительной информации о символьных переменных и предположениях на них, смотрите, Удаляют Символьные Объекты и Их Предположения.

Предыдущие команды производят комплексный выход

F = 
(pi*signIm(1i/a))/a

Функция signIm задан как:

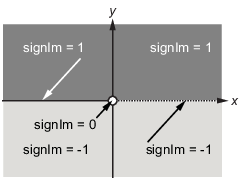
$signIm (z) = {\begin{array}{l} 1 & если Im (z) > 0, или Im (z) = 0 и z < 0 \\ 0 & если z = 0 \\ -1 & в противном случае . \end{array}$

Оценивать F в a = 1 + i, войти

g = subs(F, 1 + i)

g = 
pi*(1/2 - 1i/2)

double(g)

ans =
   1.5708 - 1.5708i

Численное интегрирование высокой точности Используя арифметику Переменной Точности

Численное интегрирование высокой точности реализовано в vpaintegral функция Symbolic Math Toolbox™. vpaintegral арифметика переменной точности использования в отличие от MATLAB integral функция, которая использует арифметику с двойной точностью.

Интегрируйте besseli(5,25*u).*exp(-u*25) при помощи обоих integral и vpaintegral. integral функция возвращает NaN и выдает предупреждение в то время как vpaintegral возвращает правильный результат.

syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);

usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)

Warning: Infinite or Not-a-Number value encountered. 
usingIntegral =
   NaN

usingVpaintegral =
0.688424

Для получения дополнительной информации смотрите vpaintegral.

Документация