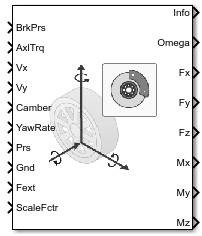
Fiala Wheel 2DOF
Колесо Fiala 2DOF колесо с диском, барабаном или сопоставленным тормозом
Описание
Блок Fiala Wheel 2DOF реализует упрощенную шину с боковой и продольной возможностью промаха на основе E. Модель [1] Fiala. Блок использует поступательную модель трения, чтобы вычислить силы и моменты во время объединенного продольного и бокового промаха, требуя меньшего количества параметров, чем блок Combined Slip Wheel 2DOF. Если вам не нуждалась в коэффициентах шины Волшебная Формула, рассматриваете использование этого блока для исследований, которые не включают обширный нелинейный объединенный боковой промах или боковую динамику. Если ваше исследование действительно требует нелинейного объединенного промаха или боковой динамики, рассмотрите использование блока Combined Slip Wheel 2DOF.
Блок определяет уровень вращения колеса, вертикальное движение и силы и моменты во всех шести степенях свободы (ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ) на основе крутящего момента автомобильной трансмиссии, тормозного давления, дорожной высоты, угла изгиба колеса и давления инфляции. Можно использовать этот блок для этих типов исследований:
Автомобильная трансмиссия и симуляции транспортного средства, которые требуют низкочастотной дороги шины и тормозных усилий для ускорения транспортного средства, торможения и вычислений сопротивления качению колеса минимальными параметрами шины.
Взаимодействие колеса с идеализированным дорожным покрытием.
Поезжайте и обрабатывающие маневры для транспортных средств, подвергающихся умеренному объединенному промаху. Для этого анализа можно соединить блок с автомобильной трансмиссией и компонентами шасси, такими как дифференциалы, приостановка и системы кузова.
Устойчивость отклонения от курса. Поскольку это анализирует, можно соединить этот блок с более подробными моделями тормозной системы.
Утомите жесткость и неперепрыгиваемые массовые взаимодействия с наземными изменениями, загрузите передачу или движение шасси с помощью блока вертикальная степень свободы.
Блок интегрирует вращательное колесо, вертикальную массу и тормозящие модели динамики. Для зависимых промахом сил шины и моменты, блок реализует модель шины Fiala.
Используйте параметр Brake Type, чтобы выбрать тормоз.
| Тормозите установку типа | Тормозите реализацию |
|---|
None
| 'none' |
Disc
| Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие |
Drum
| Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент |
Mapped
| Интерполяционная таблица, которая является функцией скорости колеса и прикладываемого тормозного давления |
Чтобы вычислить крутящий момент сопротивления качению, задайте один из этих параметров Rolling Resistance.
| Установка | Блокируйте реализацию |
|---|
None
| 'none' |
Pressure and velocity
| Метод в Пошаговой Методологии Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости. |
ISO 28580
| Метод задан в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения. |
Magic Formula
| Волшебные уравнения формулы от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов. |
Mapped torque
| Интерполяционная таблица, которая является функцией нормальной силы и оси вращения продольная скорость. |
Чтобы вычислить вертикальное движение, задайте один из этих параметров Vertical Motion.
| Установка | Блокируйте реализацию |
|---|
None
| Блок передает прикладывавшие силы шасси непосредственно до сопротивления качению и продольных вычислений силы. |
Mapped stiffness and damping
| Вертикальное движение зависит от жесткости колеса и затухания. Жесткость является функцией смещения боковой стены шины и давления. Затухание является функцией скорости боковой стены шины и давления. |
Вращательная динамика колеса
Блок вычисляет инерционный ответ колеса, удовлетворяющего:
Потери оси
Тормозите и управляйте крутящим моментом
Утомите сопротивление качению
Оснуйте контакт через дорожный шиной интерфейс
Входной крутящий момент является суммированием прикладного крутящего момента оси, тормозного момента, и момент, являющийся результатом объединенного крутящего момента шины.
В настоящий момент являясь результатом объединенного крутящего момента шины, блок реализует тяговые силы колеса и сопротивление качению с динамикой первого порядка. Сопротивлению качению параметрировали постоянную времени в терминах релаксационной длины.
Чтобы вычислить крутящий момент сопротивления качению, можно задать один из этих параметров Rolling Resistance.
| Установка | Блокируйте реализацию |
|---|
None
| Блокируйте сопротивление качению наборов, My, обнулять. |
Pressure and velocity
| Блок использует метод в SAE Пошаговая Методология Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости. А именно,
|
ISO 28580
| Блок использует метод, заданный в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения. Метод составляет нормальную загрузку, паразитную потерю и тепловые коррекции от условий испытания. А именно,
|
Magic Formula
| Блок вычисляет сопротивление качению, My, использование уравнений Magic Formula от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов. |
Mapped torque
| Для сопротивления качению, My, блок использует интерполяционную таблицу, которая является функцией нормальной силы и оси вращения продольная скорость. |
Если тормоза включены, блок определяет торможение заблокированное или разблокированное условие на основе идеализированной сухой модели трения муфты. На основе условия тупика блок реализует их трение и динамические модели.
| Если | Условие тупика | Модель трения | Динамическая модель |
|---|
| Разблокированный |
|
|
| Заблокированный |
|
|
Уравнения используют эти переменные.
| ω | Скорость вращения колеса |
| a | Независимый от скорости компонент силы |
| b | Линейный скоростной компонент силы |
| c | Квадратичный скоростной компонент силы |
| Le | Утомите релаксационную длину |
| J | Момент инерции |
| My | Крутящий момент сопротивления качению |
| Ta | Прикладной крутящий момент оси |
| Tb | Тормозной момент |
| Td | Объединенный крутящий момент шины |
| Tf | Фрикционный крутящий момент |
| Ti | Сетевой входной крутящий момент |
| Tk | Кинетический фрикционный крутящий момент |
| To | Сетевой выходной крутящий момент |
| Ts | Статический фрикционный крутящий момент |
| Fc | Прикладывавшая сила муфты |
| Fx | Продольная сила, разработанная дорогой шины, взаимодействует через интерфейс должный уменьшиться |
| Reff | Эффективный радиус муфты |
| Ro | Кольцевой диск внешний радиус |
| Ri | Кольцевой диск внутренний радиус |
| Re | Эффективный радиус шины, в то время как при загрузке и при данном давлении |
| Vx | Продольная скорость оси |
| Fz | Транспортное средство нормальная сила |
| Cr | Постоянное сопротивление качению |
| Tamb | Температура окружающей среды |
| Tmeas | Измеренная температура для постоянного сопротивления качению |
| Fpl | Паразитная потеря силы |
| Kt | Тепловой поправочный коэффициент |
| ɑ | Экспонента давления воздуха в шине |
| β | Нормальная экспонента силы |
| pi | Давление воздуха в шине |
| μs | Коэффициент статического трения |
| μk | Коэффициент кинетического трения |
Продольная сила
Блок реализует продольную силу как функцию промаха колеса относительно дорожного покрытия с помощью этих уравнений.
| Вычисление | Уравнение |
|---|
Критический промах |
|
Продольная сила |
|
Коэффициент трения |
|
Подсуньте коэффициент |
|
Уравнения используют эти переменные.
| κ' | Состояние промаха |
| Fx | Продольная сила, действующая на ось вдоль зафиксированной шиной оси X, |
| Cκ | Продольная жесткость |
| Fz | Вертикальная закрашенная фигура контакта нормальная сила вдоль зафиксированной шиной оси z, |
| μ | Коэффициент трения |
| μs | Коэффициент статического трения |
| μk | Коэффициент кинетического трения |
| κka | Всесторонний коэффициент промаха |
| α' | Подсуньте угловое состояние |
| λμ | Масштабирование трения |
Боковая сила
Блок реализует боковую силу как функцию углового состояния промаха колеса, использующего эти уравнения.
| Вычисление | Уравнение |
|---|
Критический угол промаха |
|
Боковая сила |
|
Уравнения используют эти переменные.
| α' | Подсуньте угловое состояние |
| Fy | Боковая сила, действующая на ось вдоль зафиксированной шиной оси Y, |
| Fz | Вертикальная закрашенная фигура контакта нормальная сила вдоль зафиксированной шиной оси z |
| Cɣ | Жесткость изгиба |
| Cα | Боковая жесткость на угол промаха |
| μ | Коэффициент трения |
Вертикальная динамика
Для вертикальной динамики блок реализует эти уравнения.
| Вычисление | Уравнение |
|---|
Вертикальный ответ |
|
Утомите нормальную силу |
|
Вертикальное отклонение боковой стены |
|
Уравнения используют эти переменные.
| z | Утомите отклонение вдоль зафиксированной шиной оси z |
| zgnd | Оснуйте смещение вдоль зафиксированного шиной z - ось |
| Fztire | Утомите нормальную силу вдоль зафиксированной шиной оси z |
| Fz | Вертикальная сила, действующая на ось вдоль зафиксированной шиной оси z |
| ρz | Вертикальное отклонение боковой стены вдоль зафиксированной шиной оси z |
| k | Вертикальная жесткость боковой стены |
| b | Вертикальное затухание боковой стены |
Опрокидывание, выравниваясь, и масштабирование
Эта таблица суммирует опрокидывание, выравнивание и масштабирование реализации.
| Вычисление | Реализация |
|---|
Опрокидывание момента | Модель Fiala не задает опрокидывающийся момент. Блок реализует это уравнение, требуя минимальных параметров.
|
Выравнивание момента | Блок реализует выравнивающийся момент как комбинацию затухания уровня отклонения от курса и углового состояния промаха.
|
Масштабирование трения | Чтобы варьироваться коэффициент трения, используйте ScaleFctr входной порт. |
Уравнения используют эти переменные.
| Mx | Опрокидывание момента, действуя на ось о зафиксированной шиной оси X |
| Mz | Выравнивание момента, действуя на ось о зафиксированной шиной оси z |
| Re | Эффективная закрашенная фигура контакта, чтобы вертеть поставщика услуг радиальное расстояние |
| ɣ | Угол изгиба |
| k | Вертикальная жесткость боковой стены |
| b | Вертикальное затухание боковой стены |
| Утомите скорость вращения о зафиксированной шиной оси z (уровень отклонения от курса) |
| w | Утомите ширину |
| α' | Подсуньте угловое состояние |
| bMz | Линейное сопротивление уровня отклонения от курса |
| Fy | Боковая сила, действующая на ось вдоль зафиксированной шиной оси Y |
| Cɣ | Жесткость изгиба |
| Cα | Боковая жесткость на угол промаха |
| μ | Коэффициент трения |
| Fz | Вертикальная закрашенная фигура контакта нормальная сила вдоль зафиксированной шиной оси z |
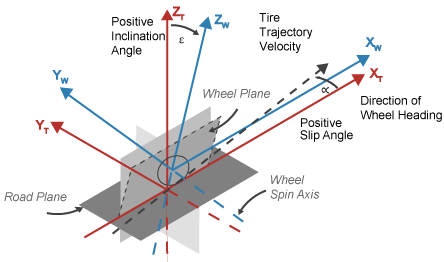
Шина и системы координат колеса
Чтобы разрешить силы и моменты, блок использует ориентацию Z-Up систем координат шины и колеса.
Утомите оси системы координат (XT, YT, ZT) фиксируются в системе координат, присоединенной к шине. Источник в контакте шины с землей.
Оси системы координат колеса (XW, YW, ZW) фиксируются в системе координат, присоединенной к колесу. Источник стоит у руля центр.
Ориентация Z-Up
Тормоза
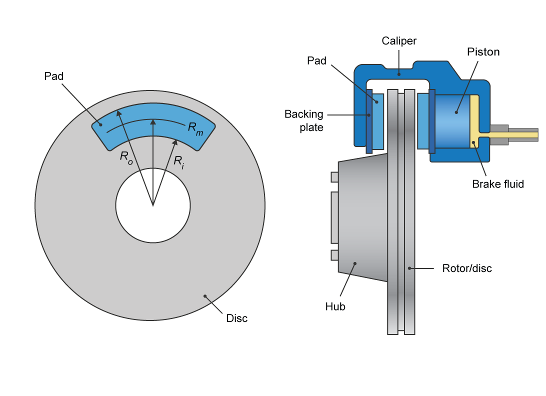
ДискЕсли вы задаете параметр Brake Type Disc, блок реализует дисковый тормоз. Этот рисунок показывает виды сбоку и виды спереди дискового тормоза.
Дисковый тормоз преобразует давление в тормозном цилиндре от тормозного цилиндра в силу. Дисковый тормоз прикладывает силу в среднем радиусе тормозной колодки.
Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.
Уравнения используют эти переменные.
| T | Момент привода |
| P | Прикладываемое тормозное давление |
| N | Скорость колеса |
| Npads | Количество тормозных колодок в блоке дискового тормоза |
| μstatic | Коэффициент статического трения пары диск-колодка |
| μ | Коэффициент кинетического трения пары диск-колодка |
| Ba | Внутренний диаметр тормозного цилиндра суппорта |
| Rm | Средний радиус тормозной колодки обеспечивает приложение на тормозном роторе |
| Ro | Внешний радиус тормозной колодки |
| Ri | Внутренний радиус тормозной колодки |
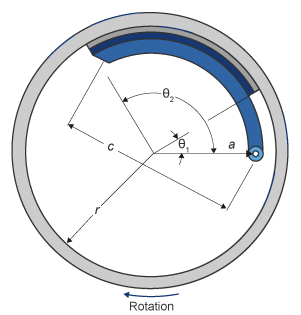
БарабанЕсли вы задаете параметр Brake Type Drum, блок реализует статический (установившийся) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двухстороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не совместно используют общий контакт стержня.
Симплексная модель барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия обуви симметричны для обеих сторон, позволяя одному набору геометрии и параметров трения использоваться для обоих ботинок.
Блок реализует уравнения, которые выведены из этих уравнений в Основных принципах Элементов Машины.
Уравнения используют эти переменные.
| T | Момент привода |
| P | Прикладываемое тормозное давление |
| N | Скорость колеса |
| μstatic | Коэффициент статического трения пары диск-колодка |
| μ | Коэффициент кинетического трения пары диск-колодка |
| Trshoe | Момент привода правого ботинка |
| Tlshoe | Момент привода левого ботинка |
| a | Расстояние от барабана сосредотачивается к центру контакта стержня обуви |
| c | Расстояние от стержня обуви прикрепляет центр, чтобы тормозить связь привода на тормозной колодке |
| r | Барабан внутренний радиус |
| Ba | Внутренний диаметр тормозного цилиндра суппорта |
| Θ1 | Угол от стержня обуви прикрепляет центр, чтобы запуститься материала тормозной колодки по обуви |
| Θ2 | Угол от стержня обуви прикрепляет центр к концу материала тормозной колодки по обуви |
СопоставленныйЕсли вы задаете параметр Brake Type Mapped, блок использует интерполяционную таблицу, чтобы определить момент привода.
Уравнения используют эти переменные.
| T | Момент привода |
| Интерполяционная таблица момента привода |
| P | Прикладываемое тормозное давление |
| N | Скорость колеса |
| μstatic | Коэффициент трения поверхности клавиатуры барабана взаимодействует через интерфейс при статических условиях |
| μ | Коэффициент трения интерфейса ротора клавиатуры диска |
Интерполяционная таблица для момента привода, , функция прикладываемого тормозного давления и скорости колеса, где:
T является моментом привода в N · m.
P является прикладываемым тормозным давлением в панели.
N является скоростью колеса в об/мин.
Порты
Входной параметр
развернуть все
BrkPrs — Тормозное давление
scalar | N- 1 вектор
Тормозное давление, в Па.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Зависимости
Чтобы включить этот порт, для параметра Brake Type, задают один из этих типов:
AxlTrq — Крутящий момент оси
scalar | N- 1 вектор
Крутящий момент оси, Ta, об оси вращения колеса, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Vx — Продольная скорость
scalar | N- 1 вектор
Ось продольная скорость, Vx, вдоль зафиксированной шиной оси X, в m/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Vy — Боковая скорость
scalar | N- 1 вектор
Скорость ответвления оси, Vy, вдоль зафиксированной шиной оси Y, в m/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Camber — Угол изгиба
scalar | N- 1 вектор
Угол изгиба, ɣ, в рад.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
YawRate — Утомите скорость вращения
scalar | N- 1 вектор
Утомите скорость вращения, r, о зафиксированной шиной оси z (уровень отклонения от курса), в rad/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Prs — Давление накачивания шин
scalar | N- 1 вектор
Давление накачивания шин, pi, в Па.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Gnd — Оснуйте смещение
scalar | N- 1 вектор
Оснуйте смещение вдоль зафиксированного шиной z - ось в m. Положительный вход производит лифт колеса.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fext — Сила оси прикладывается к шине
scalar | N- 1 вектор
Сила оси применялась к шине, Fext, вдоль зафиксированной транспортным средством оси z (положительный вход сжимает шину), в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
ScaleFctrs ScaleFactor
scalar | N- 1 вектор
Масштабный коэффициент с учетом изменений коэффициента трения.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Вывод
развернуть все
Info — Блокируйте данные
шина
Блокируйте данные, возвращенные как сигнал шины, содержащий эти значения блока.
| Сигнал | Описание | Модули |
|---|
AxlTrq
| Крутящий момент оси о зафиксированной колесом оси Y | N· |
Omega
| Скорость вращения колеса о зафиксированной колесом оси Y | рад/с |
Fx
| Продольная сила транспортного средства вдоль зафиксированной шиной оси X | N |
Fy
| Боковая сила транспортного средства вдоль зафиксированной шиной оси Y | N |
Fz
| Вертикальная сила транспортного средства вдоль зафиксированной шиной оси z | N |
Mx
| Опрокидывание момента о зафиксированной шиной оси X | N· |
My
| Крутящий момент сопротивления качению о зафиксированной шиной оси Y | N· |
Mz
| Выравнивание момента о зафиксированной шиной оси z | N· |
Vx
| Транспортное средство продольная скорость вдоль зафиксированной шиной оси X | m/s |
Vy
| Скорость ответвления транспортного средства вдоль зафиксированной шиной оси Y | m/s |
Re
| Загруженный эффективный радиус | m |
Kappa
| Продольное отношение промаха | Нет данных |
Alpha
| Угол заноса | рад |
a
| Свяжитесь с закрашенной фигурой половина длины | m |
b
| Свяжитесь с полушириной закрашенной фигуры | m |
Gamma
| Угол изгиба | рад |
psidot
| Утомите скорость вращения о зафиксированной шиной оси z (уровень отклонения от курса) | рад/с |
BrkTrq
| Момент привода о зафиксированной транспортным средством оси Y | N· |
BrkPrs
| Тормозное давление | Па |
z
| Ось вертикальное смещение вдоль зафиксированной шиной оси z | m |
zdot
| Ось вертикальная скорость вдоль зафиксированной шиной оси z | m/s |
Gnd
| Оснуйте смещение вдоль зафиксированной шиной оси z (положительный вход производит лифт колеса), | m |
GndFz
| Вертикальная сила боковой стены на земле вдоль зафиксированной шиной оси z | N |
Prs
| Давление накачивания шин | Па |
Omega — Скорость вращения колеса
scalar | N- 1 вектор
Скорость вращения колеса, ω, о зафиксированной колесом оси Y, в rad/s.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fx — Продольная сила оси
scalar | N- 1 вектор
Продольная сила, действующая на ось, Fx, вдоль зафиксированной шиной оси X, в N. Положительная сила действует, чтобы переместить транспортное средство вперед.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fy — Боковая сила оси
scalar | N- 1 вектор
Боковая сила, действующая на ось, Fy, вдоль зафиксированной шиной оси Y, в N.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Fz — Вертикальная сила оси
scalar | N- 1 вектор
Вертикальная сила, действующая на ось, Fz, вдоль зафиксированной шиной оси z, в N.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Mx — Опрокидывание момента
scalar | N- 1 вектор
Продольный момент, действуя на ось, Mx, о зафиксированной шиной оси X, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
My — Прокрутка резистивного момента
scalar | N- 1 вектор
Боковой момент, действуя на ось, My, о зафиксированной шиной оси Y, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Mz — Выравнивание момента
scalar | N- 1 вектор
Вертикальный момент, действуя на ось, Mz, о зафиксированной шиной оси z, в N · m.
Вектор является количеством колес, N, 1. Если вы вводите скалярное значение, блок принимает, что количество колес является тем.
Параметры
развернуть все
Блокируйте опции
Brake Type — Выберите тип
None | Disc | Drum | Mapped
Используйте параметр Brake Type, чтобы выбрать тормоз.
| Тормозите установку типа | Тормозите реализацию |
|---|
None
| 'none' |
Disc
| Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие |
Drum
| Симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной момент |
Mapped
| Интерполяционная таблица, которая является функцией скорости колеса и прикладываемого тормозного давления |
Rolling Resistance — Выберите тип
None (значение по умолчанию) | Pressure and velocity | ISO 28580 | Magic Formula | Mapped torque
Чтобы вычислить крутящий момент сопротивления качению, задайте один из этих параметров Rolling Resistance.
| Установка | Блокируйте реализацию |
|---|
None
| 'none' |
Pressure and velocity
| Метод в Пошаговой Методологии Coastdown для Измерения Сопротивления качению Шины. Сопротивление качению является функцией давления воздуха в шине, нормальной силы и скорости. |
ISO 28580
| Метод задан в ISO 28580:2018, Легковом автомобиле, методе измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения. |
Magic Formula
| Волшебные уравнения формулы от 4. E70 в Шине и Динамике аппарата. Волшебная формула является эмпирическим уравнением на основе подходящих коэффициентов. |
Mapped torque
| Интерполяционная таблица, которая является функцией нормальной силы и оси вращения продольная скорость. |
Зависимости
| Выбор | Параметры |
|---|
Pressure and velocity
| Velocity independent force coefficient, aMy Linear velocity force component, bMy Quadratic velocity force component, cMy Tire pressure exponent, alphaMy Normal force exponent, betaMy |
ISO 28580
| Parasitic losses force, Fpl Rolling resistance constant, Cr Thermal correction factor, Kt Measured temperature, Tmeas Parasitic losses force, Fpl Ambient temperature, Tamb |
Magic Formula
| Rolling resistance torque coefficient, QSY Longitudinal force rolling resistance coefficient, QSY2 Linear rotational speed rolling resistance coefficient, QSY3 Quartic rotational speed rolling resistance coefficient, QSY4 Camber squared rolling resistance torque, QSY5 Load based camber squared rolling resistance torque, QSY6 Normal load rolling resistance coefficient, QSY7 Pressure load rolling resistance coefficient, QSY8 Rolling resistance scaling factor, lam_My |
Mapped torque
| Spin axis velocity breakpoints, VxMy Normal force breakpoints, FzMy Rolling resistance torque map, MyMap |
Vertical Motion — Выберите тип
None (значение по умолчанию) | Mapped stiffness and damping
Чтобы вычислить вертикальное движение, задайте один из этих параметров Vertical Motion.
| Установка | Блокируйте реализацию |
|---|
None
| Блок передает прикладывавшие силы шасси непосредственно до сопротивления качению и продольных вычислений силы. |
Mapped stiffness and damping
| Вертикальное движение зависит от жесткости колеса и затухания. Жесткость является функцией смещения боковой стены шины и давления. Затухание является функцией скорости боковой стены шины и давления. |
| Выбор | Включает эти параметры |
|---|
Mapped stiffness and damping
| Wheel mass, MASS Initial tire deflection, zo Initial velocity, zdoto Initial wheel vertical velocity (wheel fixed frame), zdoto Vertical deflection breakpoints, zFz Pressure breakpoints, pFz Force due to deflection, Fzz Vertical velocity breakpoints, zdotFz Force due to velocity, Fzzdot |
Продольный и боковой
Longitudinal stiffness, Ckappa — Продольная жесткость
1e7 (значение по умолчанию) | scalar
Продольная жесткость, Cκ, в N.
Lateral stiffness per slip angle, Calpha — Боковая жесткость
4.5e4 (значение по умолчанию) | scalar
Боковая жесткость на угол промаха, Cα, в N/rad.
Camber stiffness, Cgamma — Жесткость изгиба
1e3 (значение по умолчанию) | scalar
Жесткость изгиба, Cɣ, в N/rad.
Kinematic friction, muMin — Трение
.8 scalar
Кинематическое трение, μk, безразмерный.
Static friction, muMax — Трение
1 scalar
Статическое трение, μs, безразмерный.
Longitudinal relaxation length, Lrelx длина
.05 scalar
Продольная релаксационная длина, Lrelx, в m.
Lateral relaxation length, Lrely длина
.15 scalar
Боковая релаксационная длина, Lrely, в m/rad.
Прокрутка
Rotational damping, br — Затухание
1e-3 (значение по умолчанию) | scalar
Вращательное затухание, br, в N · m·.
Rotational inertia (rolling axis), IYY — Инерция
0.74 scalar
Вращательная инерция (прокручивающий ось), IYY, в kg · м^2.
Initial rotational velocity, omegao — Скорость
0 scalar
Начальная вращательная скорость, в rad/s.
Unloaded radius, UNLOADED_RADIUS — Радиус
0.309384029954441 scalar
Разгруженный радиус, в m.
Velocity independent force coefficient, aMy — Обеспечьте коэффициент
8e-4 (значение по умолчанию) | scalar
Независимый от скорости коэффициент силы, a, в s/m.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.
Linear velocity force component, bMy — Компонент силы
.001 scalar
Линейный скоростной компонент силы, b, в s/m.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.
Quadratic velocity force component, cMy — Компонент силы
1.6e-4 (значение по умолчанию) | scalar
Квадратичный скоростной компонент силы, c, в s^2/m^2.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.
Tire pressure exponent, alphaMy — Экспонента давления
-0.003 scalar
Экспонента давления воздуха в шине, ɑ, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.
Normal force exponent, betaMy — Обеспечьте экспоненту
0.97 scalar
Нормальная экспонента силы, β, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Pressure and velocity.
Parasitic losses force, Fpl — Обеспечьте потерю
10 scalar
Паразитная потеря силы, Fpl, в N.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Rolling resistance constant, Cr — Постоянный
1e-3 (значение по умолчанию) | scalar
Постоянное сопротивление качению, Cr, в N/kN. ISO 28580 задает модуль сопротивления качению как один ньютон тягового сопротивления для каждого килоньютоны нормальной загрузки.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Thermal correction factor, Kt — Поправочный коэффициент
.008 scalar
Тепловой поправочный коэффициент, Kt, в 1/degC.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Measured temperature, Tmeas — Температура
298.15 scalar
Измеренная температура, Tmeas, в K.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Ambient temperature, Tamb — Температура
298.15 scalar
Измеренная температура, Tamb, в K.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Input ambient temperature — Выбор
off (значение по умолчанию) | on
Выберите, чтобы создать входной порт Tamb.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Rolling resistance torque coefficient, QSY1 — Закрутите коэффициент
0.007 scalar
Коэффициент крутящего момента сопротивления качению, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Longitudinal force rolling resistance coefficient, QSY2 — Обеспечьте коэффициент сопротивления
0 scalar
Продольный коэффициент сопротивления качению силы, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Linear rotational speed rolling resistance coefficient, QSY3 — Линейный коэффициент скорости
0.0015 scalar
Линейный коэффициент сопротивления качению скорости вращения, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Quartic rotational speed rolling resistance coefficient, QSY4 — Биквадратный коэффициент скорости
8.5e-05 (значение по умолчанию) | scalar
Биквадратный коэффициент сопротивления качению скорости вращения, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Camber squared rolling resistance torque, QSY5 — Крутящий момент сопротивления изгиба
0 scalar
Изгиб придал крутящему моменту сопротивления качению квадратную форму в 1/rad^2.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Load based camber squared rolling resistance torque, QSY6 — Крутящий момент нагрузочного сопротивления
0 scalar
Основанный на загрузке изгиб придал крутящему моменту сопротивления качению квадратную форму в 1/rad^2.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Normal load rolling resistance coefficient, QSY7 — Нормальный коэффициент сопротивления
0.9 scalar
Нормальный коэффициент сопротивления качению загрузки, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Pressure load rolling resistance coefficient, QSY8 — Коэффициент сопротивления давления
-0.4 scalar
Коэффициент сопротивления качению загрузки давления, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Rolling resistance scaling factor, lam_My шкала
1 scalar
Масштабный коэффициент сопротивления качению, безразмерный.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Magic Formula.
Spin axis velocity breakpoints, VxMy — Точки останова
-20:1:20 vector
Точки останова оси вращения скорости, в m/s.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Mapped torque.
Normal force breakpoints, FzMy — Точки останова
0:200:1e4 (значение по умолчанию) | vector
Нормальные точки останова силы, в N.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Mapped torque.
Rolling resistance torque map, MyMap — Интерполяционная таблица
array
Крутящий момент сопротивления качению по сравнению со скоростью оси и нормальной силой, в N · m.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance Mapped torque.
Выравнивание
Wheel width, WIDTH width
0.209
scalar
Ширина колеса, WIDTH, в m.
Linear yaw rate resistance, bMz — Сопротивление
0 | scalar
Линейное сопротивление уровня отклонения от курса, bMz, в N · m·.
Тормоз
Static friction coefficient, mu_static — Статическое трение
.3
scalar
Статический коэффициент трения, безразмерный.
Зависимости
Чтобы включить этот параметр, для параметра Brake Type, задают один из этих типов:
Kinetic friction coefficient, mu_kinetic — Кинетическое трение
.2 scalar
Кинематический коэффициент трения, безразмерный.
Зависимости
Чтобы включить этот параметр, для параметра Brake Type, задают один из этих типов:
Disc brake actuator bore, disc_abore — Расстояние скуки
.05 scalar
Привод дискового тормоза перенес в m.
Зависимости
Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.
Brake pad mean radius, Rm — Радиус
.177 scalar
Средний радиус тормозной колодки, в m.
Зависимости
Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.
Number of brake pads, num_pads количество
2 scalar
Количество тормозных колодок.
Зависимости
Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.
Drum brake actuator bore, disc_abore — Расстояние скуки
0.0508 scalar
Привод барабанного тормоза перенес в m.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Shoe pin to drum center distance, drum_a — Расстояние
0.123 scalar
Контакт обуви, чтобы барабанить расстояние между центрами, в m.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Shoe pin center to force application point distance, drum_c — Расстояние
0.212 scalar
Контакт обуви сосредотачивается, чтобы обеспечить расстояние точки приложения в m.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Drum internal radius, drum_r — Радиус
0.15 scalar
Барабан внутренний радиус, в m.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Shoe pin to pad start angle, drum_theta1 \angle
0 scalar
Контакт обуви, чтобы заполнить запускает угол в градусе.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Shoe pin to pad end angle, drum_theta2 \angle
126 scalar
Контакт обуви, чтобы заполнить угол конца, в градусе.
Зависимости
Чтобы включить параметры барабанного тормоза, выберите Drum для параметра Brake Type.
Brake actuator pressure breakpoints, brake_p_bpt — Точки останова
vector
Тормозите точки останова давления привода в панели.
Зависимости
Чтобы включить сопоставленные параметры тормоза, выберите Mapped для параметра Brake Type.
Wheel speed breakpoints, brake_n_bpt — Точки останова
vector
Точки останова скорости колеса, в об/мин.
Зависимости
Чтобы включить сопоставленные параметры тормоза, выберите Mapped для параметра Brake Type.
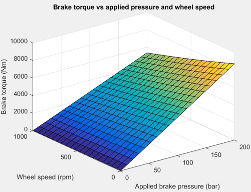
Brake torque map, f_brake_t — Интерполяционная таблица
array
Интерполяционная таблица для момента привода, , функция прикладываемого тормозного давления и скорости колеса, где:
T является моментом привода в N · m.
P является прикладываемым тормозным давлением в панели.
N является скоростью колеса в об/мин.
Зависимости
Чтобы включить сопоставленные параметры тормоза, выберите Mapped для параметра Brake Type.
Вертикальный
Wheel mass, m — Масса
9.46491996974568
scalar
Масса колеса, в kg. Используемый в вертикальных вычислениях движения.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Initial tire deflection, zo — Отклонение
0 scalar
Начальное смещение оси вдоль зафиксированной колесом оси z, в m.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Initial wheel vertical velocity (wheel fixed frame), zdoto — Скорость
0 scalar
Начальная скорость оси вдоль зафиксированной колесом оси z, в m.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Gravitational acceleration, GRAVITY — Сила тяжести
-9.81 scalar
Гравитационное ускорение, в м/с^2.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Vertical deflection breakpoints, zFz — Точки останова
[0 .01 .1] vector
Вектор из точек останова отклонения боковой стены, соответствующих таблице силы, в m.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Pressure breakpoints, pFz — Точки останова
[10000 1000000] vector
Вектор из точек данных давления, соответствующих таблице силы, в Па.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Force due to deflection, Fzz Сила
[0 1e3 1e4; 0 1e4 1e5] (значение по умолчанию) | vector
Обеспечьте из-за отклонения боковой стены и давления вдоль зафиксированной колесом оси z в N.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Vertical velocity breakpoints, zdotFz — Точки останова
[-20 0 20] scalar
Вектор из точек останова боковой стены скорости, соответствующих силе из-за скоростной таблицы, в m.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Force due to velocity, Fzzdot Сила
[500 0 -500;250 0 -250] array
Обеспечьте из-за скорости боковой стены и давления вдоль зафиксированной колесом оси z в N.
Зависимости
Чтобы включить этот параметр, установите Vertical Motion на Mapped stiffness and damping.
Симуляция
Maximum normal force, FZMAX Сила
10000
scalar
Максимальная нормальная сила, в N. Используемый со всеми вертикальными вычислениями силы.
Minimum normal force, FZMIN Сила
0 scalar
Минимальная нормальная сила, в N. Используемый со всеми вертикальными вычислениями силы.
Maximum pressure, PRESMAX — Давление
1003118 scalar
Максимальное давление, PRESMAX, в Па.
Minimum pressure, PRESMIN — Давление
9982 scalar
Минимальное давление, PRESMIN, в Па.
Max allowable slip ratio (absolute), KPUMAX — Отношение
1.5 scalar
Max допустимое (абсолютное) отношение промаха, KPUMAX, безразмерный.
Minimum allowable slip ratio (absolute), KPUMIN — Отношение
-1.5 scalar
Минимальное допустимое (абсолютное) отношение промаха, KPUMIN, безразмерный.
Max allowable slip angle (absolute), ALPMAX \angle
1.5708 scalar
Max допустимый (абсолютный) угол промаха, ALPMAX, в рад.
Minimum allowable slip angle (absolute), ALPMIN \angle
-1.5708 scalar
Минимальный допустимый (абсолютный) угол промаха, ALPMIN, в рад.
Maximum allowable camber angle, CAMMAX \angle
0.173 scalar
Максимальный допустимый угол изгиба CAMMAX, в рад.
Minimum allowable camber angle, CAMMIN \angle
-0.173 scalar
Минимальный допустимый угол изгиба, CAMMIN, в рад.
Minimum ambient temperature, TMIN — Tmin
0 scalar
Минимальная температура окружающей среды, TMIN, в K.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Maximum ambient temperature, TMAX — Tmax
400 scalar
Максимальная температура окружающей среды, TMAX, в K.
Зависимости
Чтобы создать этот параметр, выберите параметр Rolling Resistance ISO 28580.
Ссылки
[1] Fiala, E. "Seitenkrafte является Rollenden Luftreifen". VDI Zeitschrift, V.D.I.. Vol 96, 1954.
[2] Магистральный комитет по шине. Пошаговая методология Coastdown для измерения сопротивления качению шины. Стандартный J2452_199906. Варрендэйл, PA: SAE International, июнь 1999.
[3] ISO 28580:2018. Легковой автомобиль, метод измерения сопротивления качению шины по производству грузовых автомобилей и автобусов — Один тест точки и корреляция результатов измерения. ISO (Международная организация по стандартизации), 2018.
[4] Pacejka, Х. Б. Тайр и Динамика аппарата. 3-й редактор Оксфорд, Великобритания: SAE и Баттерворт-Хейнеманн, 2012.
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.
Введенный в R2019a
[1] Переизданный с разрешением Copyright © 2008 SAE International. Дальнейшее распределение этого материала не разрешено без предшествующего разрешения от SAE.