Краевые эффекты

Классически, DWT задан для последовательностей с длиной некоторой степени 2, и необходимы различные способы расширить выборки других размеров. Методы для расширения сигнала включают дополнение нуля, сглаженное дополнение, периодическое расширение и репликацию граничного значения (симметризация).

Основной алгоритм для DWT не ограничивается двухместной длиной и основан на простой схеме: свертка и субдискретизация. Как обычно, когда свертка выполняется на сигналах конечной длины, искажения границы возникают.

Расширения сигнала: дополнение нуля, симметризация и сглаженное дополнение

Чтобы иметь дело с искажениями границы, граница должна быть обработана по-другому по сравнению с другими частями сигнала.

Различные методы доступны, чтобы иметь дело с этой проблемой, называемой “вейвлетами на интервале” [1]. Эти интересные конструкции являются эффективными при теории, но являются не совсем удовлетворительными с практической точки зрения.

Часто желательно использовать простые схемы на основе расширения сигнала на контурах. Это включает расчет нескольких дополнительных коэффициентов на каждом этапе процесса разложения, чтобы получить совершенную реконструкцию. Нужно отметить, что расширение необходимо на каждом этапе процесса разложения.

Детали об объяснении этих схем находятся в Главе 8 книги Вейвлеты и Наборы фильтров Странгом и Нгуеном [2].

Доступные дополнительные режимы сигнала можно следующим образом (см. dwtmode):

Дополнение нуля ('zpd'): Этот метод используется в версии DWT, данного в предыдущих разделах, и принимает, что сигнал является нулем вне исходной поддержки.
Недостаток дополнения нуля - то, что разрывы искусственно создаются на границе.
Симметризация ('sym'): Этот метод принимает, что сигналы или изображения могут быть восстановлены вне их исходной поддержки симметричной репликацией граничного значения.
Это - режим по умолчанию вейвлета, преобразовывают в тулбокс.
Симметризация имеет недостаток искусственного создания разрывов первой производной на границе, но этот метод работает хорошо в целом на изображения.
Сглаженное дополнение порядка 1 ('spd'или 'sp1'): Этот метод принимает, что сигналы или изображения могут быть восстановлены вне их исходной поддержки простой производной экстраполяцией первого порядка: дополнение использования линейной дополнительной подгонки к первым двум и последним двум значениям.
Сглаженное дополнение работает хорошо в целом на сглаженные сигналы.
Сглаженное дополнение порядка 0 ('sp0'): Этот метод принимает, что сигналы или изображения могут быть восстановлены вне их исходной поддержки простой постоянной экстраполяцией. Для расширения сигнала это - повторение первого значения на левых и последнего значения справа.
Периодическое дополнение (1) ('ppd'): Этот метод принимает, что сигналы или изображения могут быть восстановлены вне их исходной поддержки периодическим расширением.
Недостаток периодического дополнения - то, что разрывы искусственно создаются на границе.

DWT, сопоставленный с этими пятью режимами, немного избыточен. Но IDWT гарантирует совершенную реконструкцию для любого из пяти предыдущих режимов вообще дополнительный режим, используемый для DWT.

Периодическое дополнение (2) ('per'): Если длина сигнала является нечетной, сигнал сначала расширен путем добавления дополнительной выборки, равной последнему значению справа. Затем минимальное периодическое расширение выполняется на каждой стороне. Тот же вид правила существует для изображений. Этот дополнительный режим используется для SWT (1D & 2D).

Этот последний режим производит самое маленькое разложение вейвлета длины. Но дополнительный режим, используемый для IDWT, должен быть тем же самым, чтобы гарантировать совершенную реконструкцию.

Перед рассмотрением иллюстративного примера давайте сравним некоторые свойства теоретического Дискретного Преобразования Вейвлета по сравнению с фактическим DWT.

Теоретический DWT применяется к сигналам, которые заданы на бесконечном временном интервале длины (Z). Для ортогонального вейвлета это преобразование имеет следующие желательные свойства:

Сохранение нормы
Позвольте cA, и cD быть приближением и деталью коэффициентов DWT бесконечной длины сигнализирует о X. Затем ^2-норма l сохраняется:
‖X‖2 = ‖cA‖2 + ‖cD‖2
Ортогональность
Позвольте A и D быть восстановленным приближением и деталью. Затем A и D являются ортогональными и
‖X‖2 = ‖A‖2 + ‖D‖2
Совершенная реконструкция
X = A + D

Поскольку DWT применяется к сигналам, которые заданы на временном интервале конечной длины, расширение необходимо для разложения, и усечение необходимо для реконструкции.

Гарантировать решающее свойство 3 (совершенная реконструкция) для произвольного выбора

Длина сигнала
Вейвлет
Дополнительный режим

имущества 1 и 2 могут быть утрачены. Эти свойства сохраняются для расширенного сигнала длины, обычно больше, чем длина исходного сигнала. Таким образом, только совершенное свойство реконструкции всегда сохраняется. Тем не менее, если DWT выполняется с помощью периодического дополнительного режима ('per') и если длина сигнала является делимой 2^J, где J является разложением максимального уровня, свойства 1, 2, и 3 остаются верными.

Практические факторы

Открыть скрипт

Итеративный шаг DWT состоит из фильтрации вместе с путем субдискретизации:

Применяйтесь фильтр lowpass затем прореживают два, чтобы получить коэффициенты приближения.
Применяйтесь фильтр highpass затем прореживают два, чтобы получить коэффициенты детали.

Так концептуально количество коэффициентов приближения является одной половиной количества выборок, и так же для коэффициентов детали.

В реальном мире мы имеем дело с сигналами конечной длины. С желанием применения теоретического алгоритма DWT к практическому должен быть обращен вопрос граничных условий: как сигнал должен быть расширен?

Прежде, чем исследовать различные сценарии, сохраните текущий граничный дополнительный режим.

origmodestatus = dwtmode('status','nodisplay');

Периодический, степень 2

Рассмотрите следующий пример. Загрузите noisdopp данные. Сигнал имеет 1 024 выборки, который является степенью 2. Используйте dwtmode установить дополнительный режим на периодический. Затем используйте wavedec получить уровень 3 DWT сигнала с помощью ортогонального db4 вейвлет.

load noisdopp;
x = noisdopp;
lev = 3;
wav = 'db4';
dwtmode('per','nodisp')
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         128         128         256         512        1024

Бухгалтерский векторный bk содержит количество коэффициентов уровнем. На каждом этапе количество коэффициентов детали уменьшает точно на коэффициент 2. В конце существуют $1024/2^3 = 128$ коэффициенты приближения.

Сравните $l^2$ - нормы.

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))

l2-norm difference: 9.0658e-09

Получите восстановленные приближения и детали путем установки на 0 соответствующие сегменты содействующего вектора c и взятие обратного DWT.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

Проверяйте на ортогональность.

fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))

Orthogonality difference 1.816e-08

Проверяйте на совершенную реконструкцию.

fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

Perfect reconstruction difference: 1.674e-11

Три теоретических свойства DWT сохраняются.

Периодический, не степень 2

Теперь получите трехуровневый DWT сигнала с 1 026 выборками. Используйте тот же вейвлет, и дополнительный режим выше. Количество коэффициентов на этапе n равномерно не делит длину сигнала.

x = [0 0 noisdopp];
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         129         129         257         513        1026

Проверяйте на $l^2$ - сохранение нормы, ортогональность и совершенная реконструкция.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))
fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))
fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

l2-norm difference: -1.4028
Orthogonality difference -0.3319
Perfect reconstruction difference: 1.6858e-11

Совершенной реконструкции удовлетворяют, но $l^2$ - норма и ортогональность не сохраняются.

Не периодический, степень 2

Получите трехуровневый DWT сигнала с 1 024. Используйте тот же вейвлет как выше, но на этот раз измените дополнительный режим, чтобы сглаживать расширение порядка 1. Количество коэффициентов на этапе n равномерно не делит длину сигнала.

dwtmode('sp1','nodisp')
[c,bk] = wavedec(x,lev,wav);
bk

bk =

         134         134         261         516        1026

Проверяйте на $l^2$ - сохранение нормы, ортогональность и совершенная реконструкция.

cx = c;
cx(bk(1)+1:end) = 0;
reconApp = waverec(cx,bk,wav);
cx = c;
cx(1:bk(1)) = 0;
reconDet = waverec(cx,bk,wav);

fprintf('l2-norm difference: %.5g\n',sum(x.^2)-sum(c.^2))
fprintf('Orthogonality difference %.4g\n',...
    sum(x.^2)-(sum(reconApp.^2)+sum(reconDet.^2)))
fprintf('Perfect reconstruction difference: %.5g\n',...
    max(abs(x-(reconApp+reconDet))));

l2-norm difference: -113.58
Orthogonality difference -2.678
Perfect reconstruction difference: 1.6372e-11

Снова, только совершенной реконструкции удовлетворяют.

Восстановите исходный дополнительный режим.

dwtmode(origmodestatus,'nodisplay');

Чтобы поддержать совершенную реконструкцию для произвольного выбора длины сигнала, вейвлета и дополнительного режима, мы используем системы координат вейвлетов.

Система координат является набором функций $\{\phi_k\}$ , которые удовлетворяют следующему условию: там существуйте константы $0 < A \leq B$ , таким образом, что для любой функции $f$ , неравенство системы координат содержит: $A{\|f\|}^2 \leq \Sigma_k {|\langle f,\phi_k\rangle|}^2 \leq B {\|f\|}^2.$

Функции в системе координат обычно не линейно независимы. Это означает, что функция $f$ не имеет уникального расширения в $\phi_k$ . Daubechies [3] показывает что, если $\{\tilde{\phi}_k\}$ двойная система координат и $f = \Sigma_{k\in K} c_k\phi_k$ для некоторых $c = \left(c_k\right)\in l^2(K)$ , и если не все $c_k$ равняются $\langle f,\tilde{\phi}_k\rangle$ , то $\Sigma_{k\in K}{|c_k|}^2 \geq \Sigma_{k\in K}{|\langle f,\tilde{\phi}_k\rangle|}^2$ .

Если $A = B$ , система координат называется трудной системой координат. Если $A = B = 1$ и $\|\phi_k\|^2 = 1$ для всех $\phi_k$ , система координат является ортонормированным базисом. Если $A \neq B$ , то энергия не обязательно сохраняется, и общее количество коэффициентов, может превысить длину сигнала. Если дополнительный режим является периодическим, вейвлет является ортогональным, и длина сигнала является делимой $2^J$ , где $J$ максимальный уровень разложения вейвлета, все три теоретических свойства DWT, удовлетворены.

Произвольные расширения

Скрипт Open Live Script

Интересно заметить, что, если произвольное расширение используется, и разложение выполняется с помощью прореживающей свертку схемы, совершенная реконструкция восстанавливается с помощью idwt или idwt2.

Создайте сигнал и получите фильтры, сопоставленные с db9 вейвлет.

x = sin(0.3*[1:451]);
w = 'db9';
[LoD,HiD,LoR,HiR] = wfilters(w);

Добавьте и предварительно ожидайте length(LoD) случайные числа к сигналу. Постройте исходные и расширенные сигналы.

lx = length(x);
lf = length(LoD);
ex = [randn(1,lf) x randn(1,lf)];
ymin = min(ex);
ymax = max(ex);
subplot(2,1,1)
plot(lf+1:lf+lx,x)
axis([1 lx+2*lf ymin ymax]);
title('Original Signal')
subplot(2,1,2)
plot(ex)
title('Extended Signal')
axis([1 lx+2*lf ymin ymax])

Используйте lowpass и highpass фильтры разложения вейвлета, чтобы получить одноуровневое разложение вейвлета расширенного сигнала.

la = floor((lx+lf-1)/2);
ar = wkeep(dyaddown(conv(ex,LoD)),la);
dr = wkeep(dyaddown(conv(ex,HiD)),la);

Подтвердите совершенную реконструкцию сигнала.

xr = idwt(ar,dr,w,lx);
err0 = max(abs(x-xr))

err0 = 5.4700e-11

Сравнение дополнительных различий

Теперь давайте проиллюстрируем различия между первыми тремя методами и для 1D и 2D сигналов.

Дополнение нуля

Используя приложение Wavelet Analysis мы исследуем эффекты дополнения нуля.

От подсказки MATLAB^® ввести
```
dwtmode('zpd')
```
От подсказки MATLAB ввести waveletAnalyzer.
Wavelet Analyzer появляется.
Кликните по пункту меню Wavelet 1-D. Дискретный аналитический инструмент вейвлета для 1D данных сигнала появляется.
В меню File выберите Аналитическую опцию В качестве примера и выберите Basic Signals> с db2 на уровне 5> Два соседних разрыва.
Выберите Display Mode: покажите и прокрутите.
Коэффициенты детали ясно показывают эффекты конца сигнала.
Симметричное расширение
От подсказки MATLAB ввести
```
dwtmode('sym')
```
Кликните по пункту меню Wavelet 1-D.
Дискретный аналитический инструмент вейвлета для 1D данных сигнала появляется.
В меню File выберите Аналитическую опцию В качестве примера и выберите Basic Signals> с db2 на уровне 5> Два соседних разрыва.
Выберите Display Mode: покажите и прокрутите.
Коэффициенты детали ясно показывают эффекты конца сигнала.
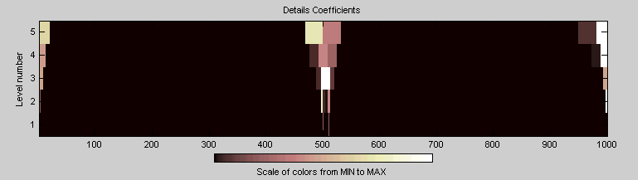
Сглаженное дополнение
От подсказки MATLAB ввести
```
dwtmode('spd')
```
Кликните по пункту меню Wavelet 1-D.
Дискретный аналитический инструмент вейвлета для 1D данных сигнала появляется.
В меню File выберите Аналитическую опцию В качестве примера и выберите Basic Signals> с db2 на уровне 5> Два соседних разрыва.
Выберите Display Mode: покажите и прокрутите.
Коэффициенты детали показывают, что эффекты конца сигнала не присутствуют, и разрывы хорошо обнаруживаются.

Отобразите расширения

Скрипт Open Live Script

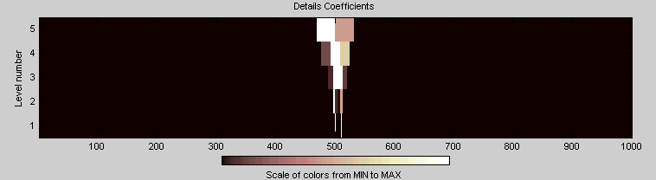
Давайте теперь рассмотрим пример изображений. Сохраните текущий дополнительный режим. Загрузите и отобразите geometry изображение.

origmodestatus = dwtmode('status','nodisplay');
load geometry
nbcol = size(map,1);
colormap(pink(nbcol))
image(wcodemat(X,nbcol))

Дополнение нуля

Установите дополнительный режим на дополнение нуля и выполните разложение изображения к уровню 3 с помощью sym4 вейвлет. Затем восстановите приближение уровня 3.

lev = 3;
wname = 'sym4';
dwtmode('zpd','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Симметричное расширение

Установите дополнительный режим на симметричное расширение и выполните разложение изображения к уровню 3 с помощью sym4 вейвлет. Затем восстановите приближение уровня 3.

dwtmode('sym','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Сглаженное дополнение

Установите дополнительный режим сглаживать дополнение и выполнять разложение изображения к уровню 3 с помощью sym4 вейвлет. Затем восстановите приближение уровня 3.

dwtmode('spd','nodisp')
[c,s] = wavedec2(X,lev,wname);
a = wrcoef2('a',c,s,wname,lev);
image(wcodemat(a,nbcol))

Восстановите исходный дополнительный режим.

dwtmode(origmodestatus,'nodisplay')

Ссылки

[1] Коэн, A. i. Daubechies, Б. Джейрт и П. Виэл. "Анализ мультиразрешения, вейвлеты и алгоритмы FAST через определенный интервал". Comptes Rendus Acad. Научный Париж Sér. A, Издание 316, стр 417–421, 1993.

[2] Странг, G. и Т. Нгуен. Вейвлеты и наборы фильтров. Веллесли, MA: Wellesley-Кембриджское нажатие, 1996.

[3] Daubechies, я. Десять лекций по вейвлетам, CBMS-NSF региональный ряд конференции в прикладной математике. Филадельфия, PA: SIAM Эд, 1992.

Смотрите также

dwtfilterbank | wavedec

Документация