Представление сигнала в конкретном основании включает нахождение уникального набора коэффициентов расширения в том основании. В то время как существует много преимуществ, чтобы сигнализировать о представлении в основании, особенно ортогональное основание, существуют также недостатки.
Способность основания обеспечить разреженное представление зависит от того, как хорошо характеристики сигнала совпадают с характеристиками базисных векторов. Например, сглаживайте непрерывные сигналы, редко представлены в основании Фурье, в то время как импульсы не. Сглаженный сигнал с изолированными разрывами редко представлен в основании вейвлета. Однако основание вейвлета не эффективно при представлении сигнала, преобразование Фурье которого имеет узкую высокочастотную поддержку.
Реальные сигналы часто содержат функции, которые запрещают разреженное представление в любом одном основании. Для этих сигналов вы хотите способность выбрать векторы из набора, не ограниченного одним основанием. Поскольку вы хотите гарантировать, что можно представлять каждый вектор на пробеле, словарь векторов, из которых вы выбираете, должен охватить пробел. Однако, потому что набор не ограничивается одним основанием, словарь не линейно независим.
Поскольку векторы в словаре не являются линейно независимым набором, представление сигнала в словаре не уникально. Однако путем создания избыточного словаря, можно расширить сигнал в наборе векторов, которые адаптируются к частоте времени или характеристикам масштаба времени сигнала. Вы свободны создать словарь, состоящий из объединения нескольких основ. Например, можно сформировать основание для пробела интегрируемых с квадратом функций, состоящих из пакетного основания вейвлета и локального основания косинуса. Пакетное основание вейвлета хорошо адаптируется к сигналам с различным поведением в различных интервалах частоты. Локальное основание косинуса хорошо адаптируется к сигналам с различным поведением в различных временных интервалах. Способность выбрать векторы из каждой из этих основ значительно увеличивает вашу способность редко представлять сигналы различными характеристиками.
Задайте словарь как набор модульной нормы элементарные базовые блоки для вашего пробела сигнала. Эти векторы модульной нормы называются атомами. Если атомы словаря охватывают целый пробел сигнала, словарь завершен.
Если атомы словаря формируют линейно зависимый набор, словарь избыточен. В большинстве приложений соответствия с преследованием словарь завершен и избыточен.
Позвольте {φk} обозначить атомы словаря. Примите, что словарь завершен и избыточен. Нет никакого уникального способа представлять сигнал от пробела как линейная комбинация атомов.
Важный вопрос - существует ли там лучший способ. Интуитивно удовлетворяющий способ выбрать лучшее представление состоит в том, чтобы выбрать φk, дающий к самым большим скалярным произведениям (в абсолютном значении) с сигналом. Например, лучший один φk
который для атома модульной нормы является величиной скалярной проекции на подпространство, заполненное φk.
Центральная проблема в соответствии с преследованием состоит в том, как вы выбираете оптимальный M - расширение термина вашего сигнала в словаре.
Позвольте Φ обозначить словарь атомов как N-by-M матрица с M> N. Если полные, избыточные словарные формы система координат для пробела сигнала, можно получить минимальный вектор коэффициентов расширения нормы L2 при помощи оператора системы координат.
Однако вектор коэффициентов, возвращенный оператором системы координат, не сохраняет разреженность. Если сигнал разрежен в словаре, коэффициенты расширения, полученные с каноническим оператором системы координат обычно, не отражают ту разреженность. Разреженность вашего сигнала в словаре является чертой, которую вы обычно хотите сохранить. Соответствие с преследованием обращается к сохранению разреженности непосредственно.
Соответствие с преследованием является жадным алгоритмом, который вычисляет лучшее нелинейное приближение к сигналу в полном, избыточном словаре. Соответствие с преследованием создает последовательность из разреженных приближений к сигналу пошагово. Позвольте Φ = {φk}, обозначают словарь атомов модульной нормы. Позвольте f быть вашим сигналом.
Запустите путем определения R0f = f
Начните соответствующее преследование путем выбора атома из словаря, который максимизирует абсолютное значение скалярного произведения с R0f = f. Обозначьте тот атом φp.
Сформируйте остаточный R1f путем вычитания ортогональной проекции R0f на пробел, заполненный φp.
Выполните итерации путем повторения шагов 2 и 3 на невязке.
Остановите алгоритм, когда вы достигнете некоторых заданный останавливающийся критерий.
В неортогональном (или основной) соответствие с преследованием, атомы словаря не являются взаимно ортогональными векторами. Поэтому вычитание последующих остаточных значений предыдущего может ввести компоненты, которые не являются ортогональными к промежутку ранее включенных атомов.
Чтобы проиллюстрировать это, рассмотрите следующий пример. Пример не предназначается, чтобы представить работу, совпадающую с алгоритмом преследования.
Считайте следующий словарь для Евклидова с 2 пробелами. Этот словарь является системой координат равной нормы.
Примите, что у вас есть следующий сигнал.
Следующая фигура иллюстрирует этот пример. Атомы словаря находятся в красном. Сигнальный вектор находится в синем.
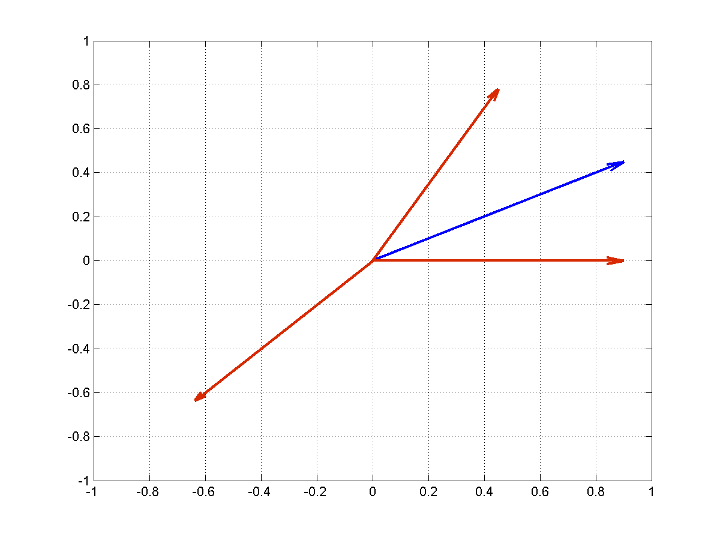
Создайте этот словарь и сигнал в MATLAB®.
dictionary = [1 0; 1/2 sqrt(3)/2; -1/sqrt(2) -1/sqrt(2)]'; x = [1 1/2]';
Вычислите внутренние (скалярные) продукты между сигналом и атомами словаря.
scalarproducts = dictionary'*x;
Самое большое скалярное произведение в абсолютном значении находится между сигналом и [-1/sqrt(2); -1/sqrt(2)]. Это ясно, потому что угол между этими двумя векторами является почти π радианами.
Сформируйте невязку путем вычитания ортогональной проекции сигнала на [-1/sqrt(2); -1/sqrt(2)] от сигнала. Затем вычислите скалярные произведения невязки (новый сигнал) с остающимися атомами словаря. Не необходимо включать [-1/sqrt(2); -1/sqrt(2)] потому что невязка является ортогональной к тому вектору конструкцией.
residual = x-scalarproducts(3)*dictionary(:,3); scalarproducts = dictionary(:,1:2)'*residual;
Самое большое скалярное произведение в абсолютном значении получено с [1;0]. Лучшими двумя атомами в словаре от двух итераций является [-1/sqrt(2); -1/sqrt(2)] и [1;0]. Если вы выполняете итерации на невязке, вы видите, что выход является более не ортогональным к первому выбранному атому. Другими словами, алгоритм ввел компонент, который не является ортогональным к промежутку первого выбранного атома. Этот факт и связанные осложнения со сходимостью спорят в пользу Ортогонального соответствия с преследованием (OMP).
В ортогональном преследовании соответствия (OMP) невязка является всегда ортогональной к промежутку атомов, уже выбранных. Это приводит к сходимости для d - размерный вектор после на большинстве шагов d.
Концептуально, можно сделать это при помощи Грамма-Schmidt, чтобы создать ортонормированный набор атомов. С ортонормированным набором атомов вы видите, что для d - размерный вектор, можно найти в большей части d ортогональные направления.
Алгоритм OMP:
Обозначьте свой сигнал f. Инициализируйте остаточный R0f = f.
Выберите атом, который максимизирует абсолютное значение скалярного произведения с R0f = f. Обозначьте тот атом φp.
Сформируйте матрицу, Φ, с ранее выбранными атомами как столбцы. Задайте оператор ортогональной проекции на промежуток столбцов Φ.
Примените оператор ортогональной проекции к невязке.
Обновите невязку.
I является единичной матрицей.
Ортогональное преследование соответствия гарантирует, что компоненты в промежутке ранее выбранных атомов не введены на последующих шагах.
Может быть в вычислительном отношении эффективно ослабить критерий, что выбранный атом максимизирует абсолютное значение скалярного произведения к менее строгому.
Это известно как слабое преследование соответствия.