Документация

Сжатие данных вейвлета

Функции сжатия данного основания вейвлета, в основном, соединяются с относительной недостаточностью представления области вейвлета для сигнала. Понятие позади сжатия основано на концепции, что регулярный компонент сигнала может быть точно аппроксимирован с помощью следующих элементов: небольшое количество коэффициентов приближения (на соответственно выбранном уровне) и некоторые коэффициенты детали.

Как шумоподавление, процедура сжатия содержит три шага:

Различие процедуры шумоподавления найдено на шаге 2. Существует два доступные подхода сжатия. Первое состоит из взятия расширения вейвлета сигнала и хранения самых больших коэффициентов абсолютного значения. В этом случае можно установить глобальный порог, эффективность сжатия или относительную квадратную эффективность восстановления нормы.

Таким образом только один параметр должен быть выбран. Второй подход состоит из применения визуально решительных зависимых уровнем порогов.

Давайте исследуем два реальных примера сжатия с помощью глобальной пороговой обработки, для данного и неоптимизированного выбора вейвлета, давайте произведем почти полное квадратное восстановление нормы для сигнала (см. Сжатие Сигнала), и для изображения (см. Сжатие изображения).

% Load electrical signal and select a part. 
load leleccum; indx = 2600:3100; 
x = leleccum(indx);
% Perform wavelet decomposition of the signal. 
n = 3; w = 'db3'; 
[c,l] = wavedec(x,n,w);
% Compress using a fixed threshold. 
thr = 35; 
keepapp = 1;
[xd,cxd,lxd,perf0,perfl2] = ...
   wdencmp('gbl',c,l,w,n,thr,'h',keepapp);

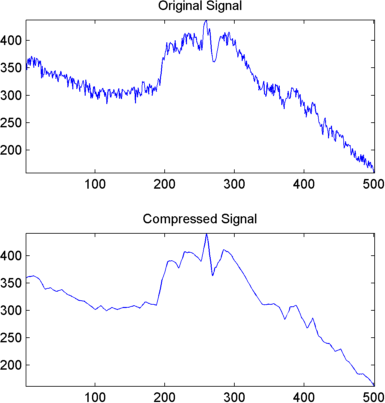
Результат является довольно удовлетворительным, не только из-за критерия восстановления нормы, но также и на визуальной точке зрения восприятия. Реконструкция использует только 15% коэффициентов.

% Load original image. 
load woman; x = X(100:200,100:200); 
nbc = size(map,1);

% Wavelet decomposition of x. 
n = 5; w = 'sym2'; [c,l] = wavedec2(x,n,w);

% Wavelet coefficients thresholding. 
thr = 20; 
keepapp = 1;
[xd,cxd,lxd,perf0,perfl2] = ...
                 wdencmp('gbl',c,l,w,n,thr,'h',keepapp);

Если представление вейвлета является слишком плотным, подобные стратегии могут использоваться в пакетной среде вейвлета, чтобы получить более разреженное представление. Можно затем определить лучшее разложение относительно соответственно выбранного подобного энтропии критерия, который соответствует выбранной цели (шумоподавление или сжатие).