Среда рассеивания вейвлета позволяет вам вывести, с минимальной настройкой, функциями низкого отклонения от временных рядов с действительным знаком и данных изображения для использования в машинном обучении и применения глубокого обучения. Функции нечувствительны к переводам входа по шкале инвариантности, которую вы задаете и непрерывны относительно деформаций. В 2D случае функции также нечувствительны к вращениям. Рассеивающаяся среда использует предопределенный вейвлет и масштабирующиеся фильтры.
Mallat, с Бруной и Анденом, вел создание математической среды для изучения сверточных нейронных архитектур [2][3][4][5]. Анден и Лостэнлен разработали эффективные алгоритмы для рассеивания вейвлета 1D [4] [6] сигналов. Oyallon разработал эффективные алгоритмы для 2D рассеивания [7]. Анден, Lostanlen и Oyallon являются основными факторами программного обеспечения ScatNet [10] и Kymatio [11] для вычисления рассеивающихся преобразований.
Mallat и другие охарактеризовали три свойства, которыми архитектуры глубокого обучения обладают для извлечения полезных функций из данных:
Многошкальные сокращения
Линеаризация иерархических симметрий
Разреженные представления
Вейвлет, рассеивающий среду, показывает все эти свойства. Вейвлет преобразовывает, линеаризуют маленькие деформации, такие как расширения путем разделения изменений через различные шкалы. Для многих естественных сигналов вейвлет преобразовывает, также обеспечивает разреженное представление. Путем объединения вейвлета преобразовывает с другими функциями рассеивающейся среды, описанной ниже, рассеивающееся преобразование производит представления данных, которые минимизируют различия в классе при сохранении discriminability через классы. Важное различие между рассеивающимся преобразованием и средами глубокого обучения - то, что фильтры заданы априорно в противоположность тому, чтобы быть изученным. Поскольку рассеивающееся преобразование не требуется, чтобы изучать ответы фильтра, можно часто использовать рассеивание успешно в ситуациях, где существует нехватка обучающих данных.
Рассеивание вейвлета преобразовывает, обрабатывает данные шаг за шагом. Выход одного этапа становится введенным для следующего этапа. Каждый этап состоит из трех операций.

Коэффициенты рассеивания нулевого порядка вычисляются простым усреднением входа. Вот структурный вид алгоритма:
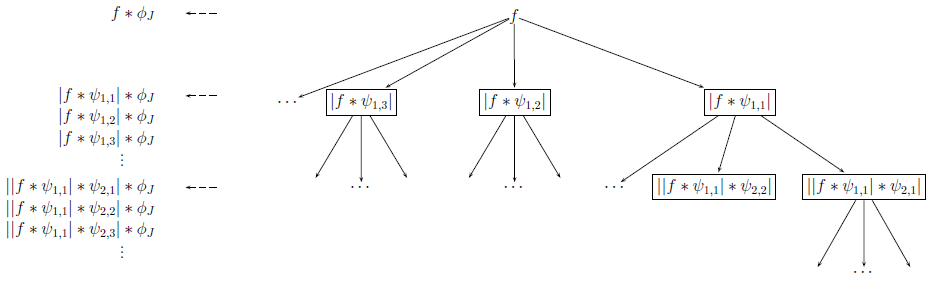
вейвлеты, масштабирующаяся функция, и входные данные. В случае данных изображения, для каждого , существует много заданных пользователями вращений вейвлета. Последовательность ребер от корня до узла упоминается как путь. Древовидные узлы являются scalogram коэффициентами. Рассеивающиеся коэффициенты являются scalogram коэффициентами, к которым применяют операцию свертки с масштабирующейся функцией . Набор рассеивающихся коэффициентов является функциями низкого отклонения, выведенными из данных. Свертка с масштабирующейся функцией является фильтрацией lowpass, и информация потеряна. Однако информация восстанавливается при вычислении коэффициентов на следующем этапе.
Чтобы извлечь функции из данных, сначала используйте waveletScattering (для временных рядов) или waveletScattering2 (для данных изображения), чтобы создать и сконфигурировать среду. Параметры, которые вы устанавливаете, включают размер шкалы инвариантности, количество наборов фильтров и количество вейвлетов на октаву в каждом наборе фильтров. В waveletScattering2 можно также определить номер вращений на вейвлет. Чтобы вывести функции из временных рядов, используйте waveletScattering функции объекта scatteringTransform или featureMatrix. Чтобы вывести функции из данных изображения, используйте waveletScattering2 функции объекта scatteringTransform или featureMatrix.
Рассеивающееся преобразование генерирует признаки итеративным способом. Во-первых, вы применяете операцию свертки к данным с масштабирующейся функцией, получить S [0], коэффициенты рассеивания нулевого порядка. Затем продолжите можно следующим образом:
Возьмите преобразование вейвлета входных данных с каждым вейвлетом, просачиваются первый набор фильтров.
Возьмите модуль каждых из отфильтрованных выходных параметров. Узлы являются scalogram, U[1].
Среднее значение каждый из модулей с масштабирующимся фильтром. Результатами являются коэффициенты рассеивания первого порядка, S[1].
Повторите процесс в каждом узле.
scatteringTransform функция возвращает рассеивание и scalogram коэффициенты. featureMatrix функция возвращает рассеивающиеся функции. Оба выходных параметров могут быть сделаны легко потребляемыми алгоритмами обучения, как продемонстрировано во Время Вейвлета, Рассеявшись для Классификации Классификации или Структуры Сигнала ECG с Рассеиванием Вейвлета Изображений.
Масштабирующийся фильтр играет важную роль в среде рассеивания вейвлета. Когда вы создаете среду рассеивания вейвлета, вы задаете шкалу инвариантности. Среда является инвариантной к переводам до шкалы инвариантности. Поддержка масштабирующейся функции определяет размер инварианта вовремя или пробела.
Для данных временных рядов шкала инвариантности является длительностью. Поддержка времени масштабирующейся функции не превышает размер инварианта. Этот график показывает поддержку масштабирующейся функции в среде со шкалой инвариантности двух секунд и частотой дискретизации 100 Гц. Также показанный действительные и мнимые части вейвлета самой грубой шкалы от первого набора фильтров. Будьте пунктуальны поддержки функций не превышают две секунды.
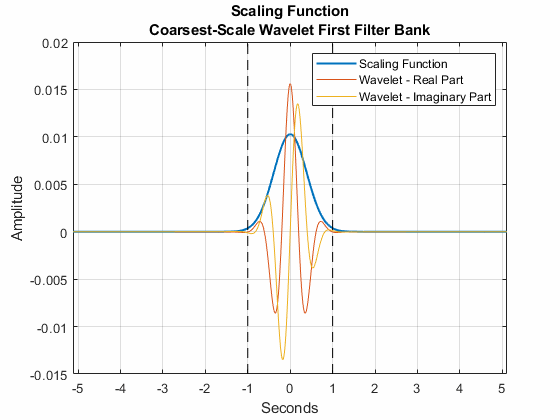
Шкала инвариантности также влияет на интервалы центральных частот вейвлетов в наборах фильтров. В наборе фильтров, созданном cwtfilterbank, полосовые центральные частоты логарифмически расположены с интервалами и пропускная способность уменьшения вейвлетов с центральной частотой.
В рассеивающейся среде, однако, поддержка времени вейвлета не может превысить шкалу инвариантности. Это свойство проиллюстрировано в графике вейвлета самой грубой шкалы. Частоты ниже, чем инвариантная шкала линейно расположены с интервалами со шкалой, сохраненной постоянной так, чтобы размер инварианта не был превышен. Следующий график показывает центральные частоты вейвлетов в первом наборе фильтров в рассеивающейся среде. Центральные частоты построены в линейных шкалах и логарифмических масштабах. Отметьте логарифмический интервал более высоких центральных частот и линейный интервал более низких центральных частот.
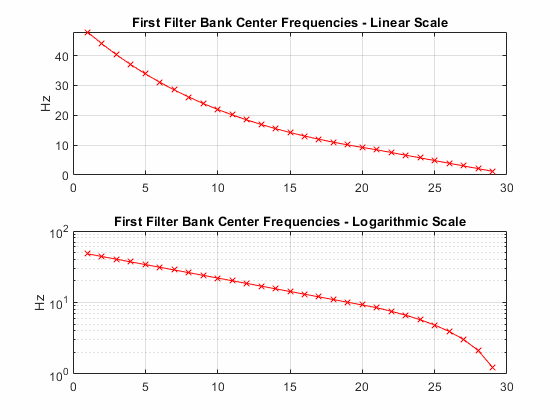
Для данных изображения шкала инвариантности задает N-by-N пространственная поддержка, в пикселях, масштабирующегося фильтра. Например, по умолчанию waveletScattering2 функция создает среду рассеивания вейвлета изображений для размера изображения 128 128 и шкалы инвариантности 64. Следующая объемная поверхностная диаграмма показывает масштабирующуюся функцию, используемую в среде. Пересекающиеся красные линии формируются 64 64 квадрат.
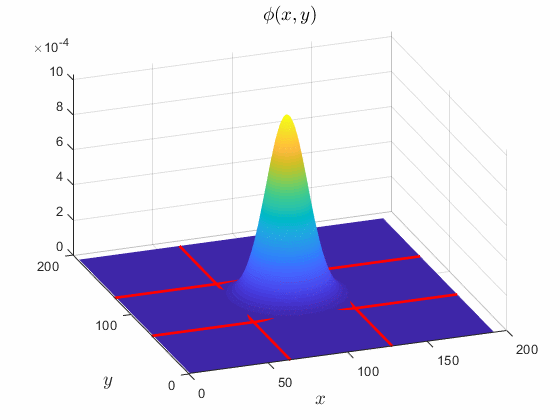
При создании среды рассеивания вейвлета, в дополнение к шкале инвариантности, вы также устанавливаете добротности для рассеивающихся наборов фильтров. Добротностью для каждого набора фильтров является количество фильтров вейвлета на октаву. Вейвлет преобразовывает, дискретизирует шкалы с помощью конкретного количества фильтров вейвлета.
Этот график показывает, что вейвлет просачивается среда, созданная waveletScattering. Шкала инвариантности является одной второй и частотой дискретизации, 200 Гц. Первый набор фильтров имеет качественное значение по умолчанию 8, и второй набор фильтров имеет добротность по умолчанию 1.
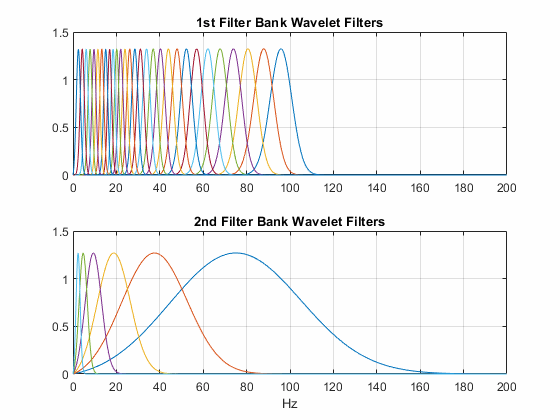
Для данных изображения большие добротности не необходимы. Большие значения также приводят к значительным вычислительным издержкам. waveletScattering2 по умолчанию создает среду с двумя наборами фильтров каждый с добротностью 1. Этот график показывает частоты центра вейвлета для среды рассеивания вейвлета изображений с двумя наборами фильтров. Первый набор фильтров имеет добротность 2, и второй набор фильтров имеет добротность 1. Количество вращений на набор фильтров равняется 6.
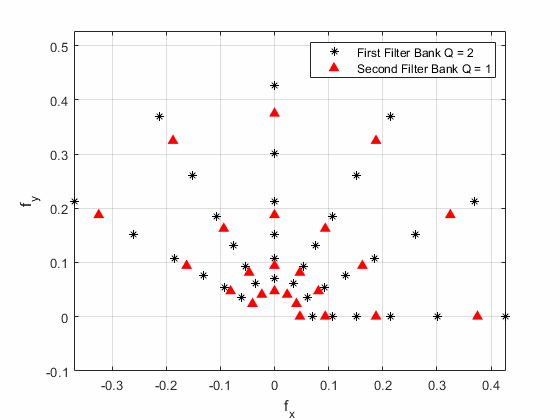
С соответствующим выбором вейвлетов рассеивающееся преобразование нерасширяемо. Энергия рассеивается, когда вы выполняете итерации через среду. Как порядок увеличения m, энергия th-порядка m scalogram коэффициенты и рассеивающиеся коэффициенты быстро сходится к 0 [3]. Энергетическое рассеяние обладает практическим преимуществом. Можно ограничить количество наборов фильтров вейвлета в среде с минимальной потерей энергии сигнала. Опубликованные результаты показывают, что энергия коэффициентов рассеивания третьего порядка может упасть ниже одного процента. Для большинства приложений среда с двумя наборами фильтров вейвлета достаточна.
Рассмотрите структурный вид среды рассеивания времени вейвлета. Предположим, что существуют вейвлеты M в первом наборе фильтров и вейвлеты N во втором наборе фильтров. Количество вейвлета просачивается, каждый набор фильтров не должен быть большим, прежде чем наивная реализация станет невыполнимой. Эффективные внедрения используют в своих интересах природу lowpass функции модуля и критически прореживают рассеивание и scalogram коэффициенты. Эти стратегии были введены впервые Andén, Mallat, Lostanlen и [4]
[6]Oyallon
[7] для того, чтобы сделать рассеивающиеся преобразования в вычислительном отношении практичными при поддержании их способности произвести представления данных низкого отклонения для изучения. По умолчанию, waveletScattering и waveletScattering2 создайте среды, которые критически прореживают коэффициенты.
[1] LeCun, Y., Б. Бозер, Дж. С. Денкер, Д. Хендерсон, Р. Э. Говард, В. Хаббард и Л. Д. Джекель. "Рукописное Распознавание Цифры с Сетью Обратной связи". В Усовершенствованиях в Нейронных Системах обработки информации (NIPS 1989) (Д. Турецкий, редактор). 396–404. Denver, CO: Морган Кофманн, Vol 2, 1990.
[2] Mallat, S. "Рассеивание Инварианта группы". Коммуникации в Чистой и Прикладной математике. Издание 65, Номер 10, 2012, стр 1331–1398.
[3] Бруна, J. и С. Маллэт. "Инвариантные Сети Свертки Рассеивания". Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 35, Номер 8, 2013, стр 1872–1886.
[4] Andén, J. и С. Маллэт. "Глубоко Рассеивание Спектра". Транзакции IEEE на Обработке сигналов. Издание 62, Номер 16, 2014, стр 4114–4128.
[5] Mallat, S. "Изучая глубоко сверточные сети". Философские Транзакции Королевского общества A. Объем 374: 20150203, 2016, стр 1–16. dx.doi.org/10.1098/rsta.2015.0203.
[6] Lostanlen, V. Scattering.m — тулбокс MATLAB для рассеивания вейвлета. https://github.com/lostanlen/scattering.m.
[7] Уаяллон, Эдуард. Веб-страница Эдуарда Уаяллона. https://edouardoyallon.github.io/.
[8] Sifre, L. и С. Маллэт. "Твердое движение, Рассеивающееся для Классификации Структуры". предварительная печать arXiv. 2014, стр 1–19. https://arxiv.org/abs/1403.1687.
[9] Sifre, L. и С. Маллэт. "Вращение, масштабирование и инвариант деформации, рассеивающийся для дискриминации структуры". 2 013 Конференций по IEEE по Компьютерному зрению и Распознаванию образов. 2013, стр 1233–1240.
[10] ScatNet. https://www.di.ens.fr/data/software/scatnet/.
[11] Kymatio. https://www.kymat.io/.
waveletScattering | waveletScattering2