Эквализация

Эквализация (EQ) является процессом взвешивания спектра частоты звукового сигнала.

Можно использовать эквализацию для:

Улучшите аудиозаписи
Анализируйте спектральное содержимое

Типы эквализации включают:

Lowpass и фильтры highpass – Ослабляют содержимое высокочастотной и низкой частоты, соответственно.
Низкая полка и эквалайзеры высокой полки – Повышение или частоты сокращения одинаково выше или ниже желаемого предела.
Параметрические эквалайзеры – Выборочно повышают или сокращают диапазоны частот. Также известный как худые фильтры.
Графические эквалайзеры – Выборочно повышают или сокращают октаву или дробные диапазоны частот октавы. У полос есть стандартизированные центральные частоты. Графические эквалайзеры являются особым случаем параметрических эквалайзеров.

Этот пример описывает, как Audio Toolbox™ реализует функции проекта: designParamEQ, designShelvingEQ, и designVarSlopeFilter. multibandParametricEQ Система object™ комбинирует функции создания фильтра в многополосный параметрический эквалайзер. graphicEQ Системный объект комбинирует функции создания фильтра и octaveFilter Системный объект для стандартизированной графической эквализации. Для примера, фокусируемого на использовании функций проекта в MATLAB^®, см. Проект Параметрического эквалайзера.

Проект эквализации Используя Audio Toolbox

Тип эквалайзера и расчетные параметры Примеры ответа величины

Тип эквалайзера и расчетные параметры	Примеры ответа величины
Использование `designVarSlopeFilter` создать фильтры highpass и lowpass. Расчетные параметры `designVarSlopeFilter` включение: Нормированная частота среза Наклон (дБ/октава)	Lowpass	Highpass
Использование `designShelvingEQ` создать эквалайзеры низкой полки и высокой полки Расчетные параметры `designShelvingEQ` включение: Получите (дБ) Нормированная частота среза Наклон (дБ/октава)	Низкая полка	Высокая полка
Использование `designParamEQ` создать параметрические эквалайзеры. Можно спроектировать параметрические эквалайзеры одно полосы или каскад параметрических эквалайзеров. Используя каскад параметрических эквалайзеров позволяет вам настроить свою частотную характеристику с точностью. Расчетные параметры `designParamEQ` включение: Количество полос эквалайзера Получите (дБ) Нормированная пропускная способность Нормированная центральная частота Порядок фильтра	Параметрический эквалайзер	Каскад параметрических эквалайзеров

Использование designVarSlopeFilter создать фильтры highpass и lowpass.

Расчетные параметры designVarSlopeFilter включение:

Нормированная частота среза
Наклон (дБ/октава)

Lowpass

Highpass

Использование designShelvingEQ создать эквалайзеры низкой полки и высокой полки

Расчетные параметры designShelvingEQ включение:

Получите (дБ)
Нормированная частота среза
Наклон (дБ/октава)

Низкая полка

Высокая полка

Использование designParamEQ создать параметрические эквалайзеры. Можно спроектировать параметрические эквалайзеры одно полосы или каскад параметрических эквалайзеров. Используя каскад параметрических эквалайзеров позволяет вам настроить свою частотную характеристику с точностью.

Расчетные параметры designParamEQ включение:

Количество полос эквалайзера
Получите (дБ)
Нормированная пропускная способность
Нормированная центральная частота
Порядок фильтра

Параметрический эквалайзер

Каскад параметрических эквалайзеров

Создание фильтра EQ

Использование функций проекта Audio Toolbox билинейное преобразовывает метод создания цифровых фильтров, чтобы определить ваши коэффициенты эквалайзера. В билинейном преобразовывают метод, вас:

Выберите аналоговый прототип.
Задайте параметры создания фильтра.
Выполните билинейное преобразование.

Аналоговый прототип Низкой Полки

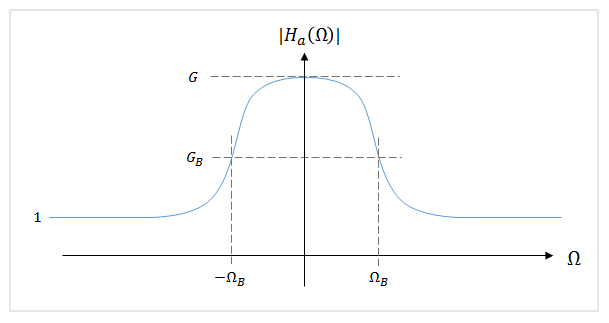
Audio Toolbox использует старший проект параметрического эквалайзера, представленный в [1]. В этом методе разработки аналоговый прототип взят, чтобы быть Фильтром Баттерворта низкой полки:

$H_{a} (s) = {[\frac{g β + s}{β + s}]}^{r} \prod_{i = 1}^{L} [\frac{g^{2} β^{2} + 2 g s_{i} β s + s^{2}}{β^{2} + 2 s_{i} β s + s^{2}}]$

$• L$ = Количество аналоговых разделов SOS

$• N$ = Аналоговый порядок фильтра

$• r = {\begin{matrix} 0 N даже \\ 1 N нечетный \end{matrix}$

$• g = G^{1 / N}$

$• β = Ω_{B} \times {(\sqrt{\frac{G^{2} - G_{B}^{2}}{G_{B}^{2} - 1}})}^{- \frac{1}{N}} = \tan (π \frac{Δ ω}{2}) \times {(\sqrt{\frac{G^{2} - G_{B}^{2}}{G_{B}^{2} - 1}})}^{- \frac{1}{N}}$ , где Δω является желаемой цифровой пропускной способностью

$• s_{i} = \sin (\frac{(2 i - 1) π}{2 N}), i = 1, 2, ..., L$

Для параметрических эквалайзеров аналоговый прототип уменьшается путем установки усиления пропускной способности на квадратный корень из пикового усиления (G _B = sqrt(G)).

После того, как расчетные параметры заданы, аналоговый прототип преобразовывается непосредственно к желаемому цифровому эквалайзеру полосовым билинейным преобразованием:

$s = \frac{1 - 2 \cos (ω_{0}) z^{- 1} + z^{- 2}}{1 - z^{- 2}}$

_ω0 является желаемой цифровой центральной частотой.

Это преобразование удваивает порядка фильтра. Каждый аналоговый раздел первого порядка становится цифровым разделом второго порядка. Каждый аналоговый раздел второго порядка становится четвертым порядком цифровой раздел. Audio Toolbox всегда вычисляет четвертый порядок цифровые разделы, что означает, что возврат секций второго порядка требует расчета корней и менее эффективен.

Цифровые коэффициенты

Цифровая передаточная функция реализована как каскад разделов четвертого порядка и второго порядка.

$H (z) = {[\frac{b_{00} + b_{01} z^{- 1} + b_{02} z^{- 2}}{1 + a_{01} z^{- 1} + a_{02} z^{- 2}}]}^{r} \prod_{i = 1}^{L} [\frac{b_{i 0} + b_{i 1} z^{- 1} + b_{i 2} z^{- 2} + b_{i 3} z^{- 3} + b_{i 4} z^{- 4}}{1 + a_{i 1} z^{- 1} + a_{i 2} z^{- 2} + a_{i 3} z^{- 3} + a_{i 4} z^{- 4}}]$

Коэффициенты даны путем выполнения полосового билинейного преобразования на аналоговом прототипном проекте.

Коэффициенты секции второго порядка	Коэффициенты раздела четвертого порядка
$\begin{array}{l} D_{0} = β + 1 \\ b_{00} = (1 + g β) / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = (1 - g β) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - β) / D_{0} \end{array}$	$\begin{array}{l} D_{i} = β^{2} + 2 s_{i} β + 1 \\ b_{i 0} = (g^{2} β^{2} + 2 g s_{i} β + 1) / D_{i} \\ b_{i 1} = - 4 c_{0} (1 + g s_{i} β) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - g^{2} β^{2}) / D_{i} \\ b_{i 3} = - 4 c_{0} (1 - g s_{i} β) / D_{i} \\ b_{i 4} = (g^{2} β^{2} - 2 g s_{i} β + 1) / D_{i} \\ a_{i 1} = - 4 c_{0} (1 + s_{i} β) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - β^{2}) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} β) / D_{i} \\ a_{i 4} = (β^{2} - 2 s_{i} β + 1) / D_{i} \end{array}$

Коэффициенты секции второго порядка

Коэффициенты раздела четвертого порядка

$\begin{array}{l} D_{0} = β + 1 \\ b_{00} = (1 + g β) / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = (1 - g β) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - β) / D_{0} \end{array}$

$\begin{array}{l} D_{i} = β^{2} + 2 s_{i} β + 1 \\ b_{i 0} = (g^{2} β^{2} + 2 g s_{i} β + 1) / D_{i} \\ b_{i 1} = - 4 c_{0} (1 + g s_{i} β) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - g^{2} β^{2}) / D_{i} \\ b_{i 3} = - 4 c_{0} (1 - g s_{i} β) / D_{i} \\ b_{i 4} = (g^{2} β^{2} - 2 g s_{i} β + 1) / D_{i} \\ a_{i 1} = - 4 c_{0} (1 + s_{i} β) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - β^{2}) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} β) / D_{i} \\ a_{i 4} = (β^{2} - 2 s_{i} β + 1) / D_{i} \end{array}$

Биквадратный Случай. В биквадратном случае, когда N = 1, коэффициенты уменьшают до:

$\begin{array}{l} D_{0} = \frac{Ω_{B}}{\sqrt{G}} + 1 \\ b_{00} = (1 + Ω_{B} \sqrt{G}) / D_{0}, b_{01} = - 2 \cos (ω_{0}) / D_{0}, b_{02} = (1 - Ω_{B} \sqrt{G}) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0}, a_{02} = (1 - \frac{Ω_{B}}{\sqrt{G}}) / D_{0} \end{array}$

Денормализовывание a ₀₀ коэффициентов и создание замен A =sqrt(G), $Ω_{B} ≅ α$ дает к знакомым худым коэффициентам EQ, описанным в [2].

Орфэнидис отмечает аппроксимированную эквивалентность Ω _B и $α$ в [1].

При помощи тригонометрических тождеств,

$Ω_{B} = \tan (\frac{Δ ω}{2}) = \sin (ω_{0}) \sinh (\frac{\ln 2}{2} B),$

где B играет роль эквивалентной пропускной способности октавы.

Бристоу-Джонсон получил приближенное решение для B в [4]:

$B = \frac{ω_{0}}{\sin ω_{0}} \times B W$

Заменение приближением для B в уравнение Ω_B дает к определению $α$ в [2]:

$α = \sin (ω_{0}) \sinh (\frac{\ln 2}{2} \times \frac{ω_{0}}{\sin ω_{0}} \times B W)$

Lowpass и создание фильтра Highpass

Аналоговый прототип Низкой Полки

Чтобы спроектировать lowpass и фильтры highpass, Audio Toolbox использует особый случай создания фильтра для параметрических эквалайзеров. В этом проекте пиковое усиление, G, установлено в 0, и G_B2 установлен в 0,5 (сокращение на-3 дБ). Частота среза фильтра lowpass соответствует 1 – Ω _B. Частота среза фильтра highpass соответствует _ΩB.

Цифровые коэффициенты

Таблица суммирует результаты полосового билинейного преобразования. Цифровая центральная частота, ω ₀, установлена в π для фильтров lowpass и 0 для фильтров highpass.

Коэффициенты раздела второго порядка	Четвертые коэффициенты раздела порядка
$\begin{array}{l} D_{0} = 1 + \tan (π \frac{Δ ω}{2}) \\ b_{00} = 1 / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = 1 / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - \tan (π \frac{Δ ω}{2})) / D_{0} \end{array}$	$\begin{array}{l} D_{i} = \tan^{2} (π \frac{Δ ω}{2}) + 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1 \\ b_{i 0} = 1 / D_{i} \\ b_{i 1} = - 4 \cos (ω_{0}) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0})) / D_{i} \\ b_{i 3} = - 4 \cos {(ω_{0})}_{0} / D_{i} \\ b_{i 4} = 1 / D_{i} \\ a_{i 1} = - 4 \cos (ω_{0}) (1 + s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - \tan^{2} (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 4} = (\tan^{2} (π \frac{Δ ω}{2}) - 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1) / D_{i} \end{array}$

Коэффициенты раздела второго порядка

Четвертые коэффициенты раздела порядка

$\begin{array}{l} D_{0} = 1 + \tan (π \frac{Δ ω}{2}) \\ b_{00} = 1 / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = 1 / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - \tan (π \frac{Δ ω}{2})) / D_{0} \end{array}$

$\begin{array}{l} D_{i} = \tan^{2} (π \frac{Δ ω}{2}) + 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1 \\ b_{i 0} = 1 / D_{i} \\ b_{i 1} = - 4 \cos (ω_{0}) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0})) / D_{i} \\ b_{i 3} = - 4 \cos {(ω_{0})}_{0} / D_{i} \\ b_{i 4} = 1 / D_{i} \\ a_{i 1} = - 4 \cos (ω_{0}) (1 + s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - \tan^{2} (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 4} = (\tan^{2} (π \frac{Δ ω}{2}) - 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1) / D_{i} \end{array}$

Откладывание создания фильтра

Аналоговый прототип

Audio Toolbox реализует отлогое создание фильтра, представленное в [2]. В этом проекте аналоговые прототипы высокой полки и низкой полки представлены отдельно:

$H_{L} (s) = A (\frac{A s^{2} + (\frac{\sqrt{A}}{Q}) s + 1}{s^{2} + (\frac{\sqrt{A}}{Q}) s + A}) H_{H} (s) = A (\frac{s^{2} + (\frac{\sqrt{A}}{Q}) s + A}{A s^{2} + (\frac{\sqrt{A}}{Q}) s + 1})$

Для компактности аналоговым фильтрам дарят переменные A и Q. Можно преобразовать A и Q к доступным расчетным параметрам Audio Toolbox:

$\begin{array}{l} A = 10^{G / 40} \\ \frac{1}{Q} = \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2} \end{array}$

После того, как вы зададите расчетные параметры, аналоговый прототип преобразовывается к желаемому цифровому отлогому фильтру по билинейному преобразованию с предварительным деформированием:

$s = (\frac{z - 1}{z + 1}) \times (\frac{1}{\tan (\frac{ω_{0}}{2})})$

Цифровые коэффициенты

Таблица суммирует результаты билинейного преобразования с предварительным деформированием.

Низкая полка	Высокая полка	Промежуточные переменные
$\begin{array}{l} b_{0} = A ((A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = 2 A ((A - 1) - (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = - 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$	$\begin{array}{l} b_{0} = A ((A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = - 2 A ((A - 1) + (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$	$\begin{array}{l} α = \frac{\sin (ω_{0})}{2} \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2 A} \\ ω_{0} = 2 π \frac{C u t o f f F r e q u e n c y}{F s} \end{array}$

Низкая полка

Высокая полка

Промежуточные переменные

$\begin{array}{l} b_{0} = A ((A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = 2 A ((A - 1) - (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = - 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$

$\begin{array}{l} b_{0} = A ((A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = - 2 A ((A - 1) + (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$

$\begin{array}{l} α = \frac{\sin (ω_{0})}{2} \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2 A} \\ ω_{0} = 2 π \frac{C u t o f f F r e q u e n c y}{F s} \end{array}$

Ссылки

[1] Orfanidis, Софокл Дж. "Старший Цифровой Проект Параметрического эквалайзера". Журнал Общества звукоинженеров. Издание 53, ноябрь 2005, стр 1026–1046.

[2] Бристоу-Джонсон, Роберт. "Формулы поваренной книги для Аудио Коэффициенты Фильтра EQ Biquad". Полученный доступ 02 марта 2016. http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt.

[3] Orfanidis, Софокл Дж. Введение в обработку сигналов. Englewood Cliffs, NJ: Prentice Hall, 2010.

[4] Бристоу-Джонсон, Роберт. "Эквивалентность различных методов вычисления коэффициентов Biquad для аудио параметрических эквалайзеров". Представленный в 97-м соглашении AES, Сан-Франциско, ноябрь 1994, предварительная печать AES 3906.

Документация