Регулирование LQG: тематическое исследование металлопрокатного завода

Обзор этого Тематического исследования

Это тематическое исследование демонстрирует использование Design Tool LQG в приложении управления процессом. Цель состоит в том, чтобы отрегулировать горизонтальную и вертикальную толщину луча, произведенного горячим стальным металлопрокатным заводом. Этот пример адаптируется от [1]. Полной моделью объекта управления является MIMO, и пример показывает преимущество прямого проекта MIMO LQG по отдельным проектам SISO для каждой оси. Ввод

milldemo

в командной строке, чтобы запустить эту демонстрацию в интерактивном режиме.

Процесс и возмущения

Металлопрокатный завод используется, чтобы сформировать прямоугольные лучи горячего металла. Желаемая исходящая форма коротко изложена ниже.

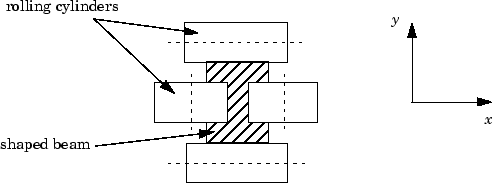
Эта форма впечатлена двумя парами прокручивающихся цилиндров (один на ось) расположенный гидравлическими приводами. Разрыв между этими двумя цилиндрами делается перекличку разрыв.

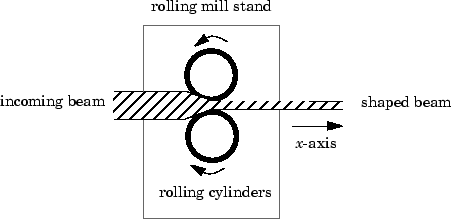
Цель состоит в том, чтобы обеспечить толщину луча вдоль x- и осей y- в допусках гарантии качества. Изменения выходной толщины могут явиться результатом следующего:

Изменения толщины/твердости входящего луча
Эксцентриситет в прокручивающихся цилиндрах

Управление с обратной связью необходимо, чтобы уменьшать эффект этих воздействий. Поскольку разрыв крена не может быть измерен близко к фрезе, стоят, прокручивающаяся сила используется вместо этого для обратной связи.

Входное воздействие толщины моделируется как фильтр нижних частот, управляемый белым шумом. Воздействие эксцентриситета является приблизительно периодическим, и его частота является функцией прокручивающейся скорости. Разумная модель для этого воздействия является полосовым фильтром второго порядка, управляемым белым шумом.

Это приводит к следующей типовой модели для каждой оси процесса прокрутки.

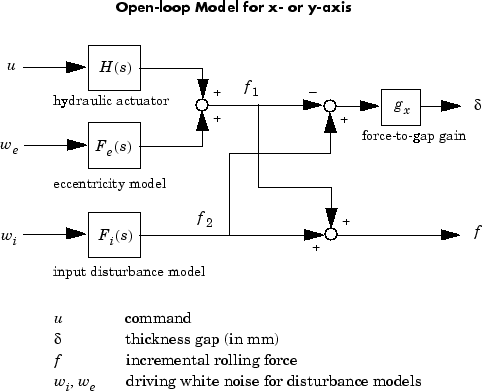
Измеренное изменение силы прокрутки f является комбинацией инкрементной силы, обеспеченной гидравлическим приводом и воздействия, обеспечивает из-за эксцентриситета и входного изменения толщины. Обратите внимание на то, что:

Выходные параметры H (s), _Fe (s) и _Fi (s) являются инкрементными силами, поставленными каждым компонентом.
Увеличение гидравлического или силы эксцентриситета уменьшает выходной разрыв толщины δ.
Увеличение входной толщины увеличивает этот разрыв.

Данные модели для каждой оси получены в итоге ниже.

Данные модели для оси X

$\begin{array}{l} H_{x} (s) = \frac{2.4 \times 10^{8}}{s^{2} + 72 s + 90^{2}} \\ F_{i x} (s) = \frac{10^{4}}{s + 0.05} \\ F_{e x} (s) = \frac{3 \times 10^{4} s}{s^{2} + 0.125 s + 6^{2}} \\ g_{x} = 10^{- 6} \end{array}$

Данные модели для оси Y

$\begin{array}{l} H_{y} (s) = \frac{7.8 \times 10^{8}}{s^{2} + 71 s + 88^{2}} \\ F_{i y} (s) = \frac{2 \times 10^{4}}{s + 0.05} \\ F_{e y} (s) = \frac{10^{5} s}{s^{2} + 0.19 s + {9.4}^{2}} \\ g_{y} = 0.5 \times 10^{- 6} \end{array}$

Проект LQG для оси X

Как первое приближение, проигнорируйте перекрестную связь между x - и y - оси и обработайте каждую ось независимо. Таким образом, спроектируйте одну SISO регулятор LQG для каждой оси. Цель проекта состоит в том, чтобы уменьшать изменения толщины _δx и _δy из-за эксцентриситета и вводить воздействия толщины.

Начните с x - ось. Сначала задайте компоненты модели, когда передаточная функция возражает.

% Hydraulic actuator (with input "u-x")
Hx = tf(2.4e8,[1 72 90^2],'inputname','u-x')

% Input thickness/hardness disturbance model
Fix = tf(1e4,[1 0.05],'inputn','w-ix')

% Rolling eccentricity model
Fex = tf([3e4 0],[1 0.125 6^2],'inputn','w-ex')

% Gain from force to thickness gap
gx = 1e-6;

Затем создайте модель разомкнутого контура, показанную в Процессе и Возмущениях. Вы могли использовать функциональный connect с этой целью, но легче создать эту модель элементарным append и series связи.

% I/O map from inputs to forces f1 and f2
Px = append([ss(Hx) Fex],Fix)

% Add static gain from f1,f2 to outputs "x-gap" and "x-force" 
Px = [-gx gx;1 1] * Px

% Give names to the outputs:
set(Px,'outputn',{'x-gap' 'x-force'})

Примечание

Чтобы получить минимальную реализацию пространства состояний, всегда преобразуйте модели передаточной функции в пространство состояний прежде, чем соединить их. Объединение передаточных функций и затем преобразование в пространство состояний могут произвести неминимальные модели в пространстве состояний.

Переменная Px теперь содержит модель в пространстве состояний разомкнутого контура вместе с именами ввода и вывода.

Px.inputname

ans = 
    'u-x'
    'w-ex'
    'w-ix'

Px.outputname

ans = 
    'x-gap'
    'x-force'

Второй выход 'x-force' прокручивающееся измерение силы. Регулятор LQG будет использовать это измерение, чтобы управлять гидравлическим приводом и уменьшать вызванные воздействием изменения толщины _δx.

Проект LQG включает два шага:

Спроектируйте усиление полной обратной связи состояния, которое минимизирует критерий качества работы LQ формы
$J (u_{x}) = \int_{0}^{\infty} {q δ_{x}^{2} + r u_{x}^{2}} d t$
Спроектируйте Фильтр Калмана, который оценивает вектор состояния, учитывая измерения силы 'x-force'.

Критерий производительности J (_ux) штрафует низкие частоты и высокие частоты одинаково. Поскольку низкочастотные изменения вызывают первоочередное беспокойство, устраняют высокочастотное содержимое _δx с lowpass, фильтруют 30 / (s + 30) и используют отфильтрованное значение в критерии производительности LQ.

lpf = tf(30,[1 30])

% Connect low-pass filter to first output of Px
Pxdes = append(lpf,1) * Px
set(Pxdes,'outputn',{'x-gap*' 'x-force'})

% Design the state-feedback gain using LQRY and q=1, r=1e-4
kx = lqry(Pxdes(1,1),1,1e-4)

Примечание

lqry ожидает, что все входные параметры будут командами и всеми выходными параметрами, чтобы быть измерениями. Здесь команда 'u-x' и измерение 'x-gap*' (отфильтрованный разрыв), первый вход и первый выход Pxdes. Следовательно, используйте синтаксис Pxdes(1,1) задавать только отношение ввода-вывода между 'u-x' и 'x-gap*'.

Затем спроектируйте Оценку состояния фильтра Калмана с функциональным kalman. Шум процесса

$w_{x} = [\begin{array}{l} w_{e x} \\ w_{i x} \end{array}]$

имеет модульную ковариацию конструкцией. Установите ковариацию шума измерения на 1 000 ограничивать высокочастотное усиление и сохранять только измеренный выход 'x-force' для проекта средства оценки.

estx = kalman(Pxdes(2,:),eye(2),1000)

Наконец, соединитесь, обратная связь состояния получают kx и средство оценки состояния estx сформировать регулятор LQG.

Regx = lqgreg(estx,kx)

Это завершает проект LQG для x −axis.

Давайте посмотрим на регулятор, Предвещают ответ между 0,1 и 1 000 рад/секунда.

h = bodeplot(Regx,{0.1 1000})
setoptions(h,'PhaseMatching','on')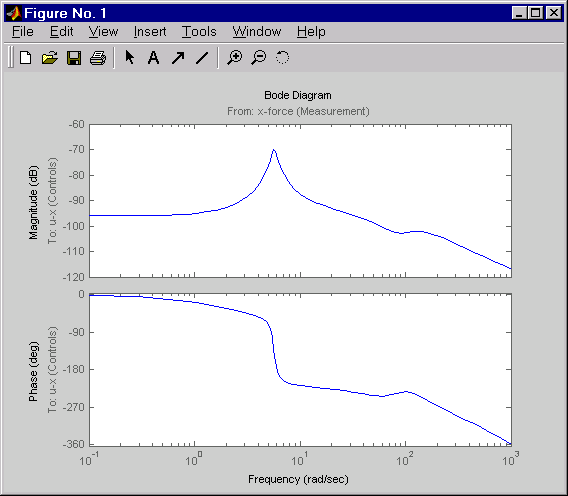

Фазовый отклик имеет интересную физическую интерпретацию. Во-первых, рассмотрите увеличение входной толщины. Это низкочастотное воздействие повышает и выходную толщину и прокручивающий силу. Поскольку фаза регулятора приблизительно ^0o в низких частотах, обратная связь затем соответственно реагирует путем увеличения гидравлической силы, чтобы возместить увеличение толщины. Теперь рассмотрите эффект эксцентриситета. Эксцентриситет вызывает колебания разрыва крена (разрыв между прокручивающимися цилиндрами). Когда разрыв крена минимален, прокручивающиеся увеличения силы и толщина луча уменьшается. Гидравлическая сила должна затем уменьшаться (отрицательная обратная связь силы), чтобы восстановить желаемую толщину. Это точно, что делает регулятор LQG, когда его фаза спадает ^до-180o около собственной частоты воздействия эксцентриситета (6 рад/секунда).

Затем сравните открытое - и ответы с обратной связью от воздействия до разрыва толщины. Используйте feedback замкнуть круг. Чтобы помочь задать связь обратной связи, посмотрите на имена ввода-вывода объекта Px и регулятор Regx.

Px.inputname
ans = 
    'u-x'
    'w-ex'
    'w-ix'
 
Regx.outputname
ans = 
    'u-x'
 
Px.outputname
ans = 
    'x-gap'
    'x-force'
 
Regx.inputname
ans = 
    'x-force'

Это указывает, что необходимо соединить первый вход и второй выход Px к регулятору.

clx = feedback(Px,Regx,1,2,+1)       % Note: +1 for positive feedback

Вы теперь готовы сравнить открытое - и с обратной связью Предвещают ответы от воздействия до разрыва толщины.

h = bodeplot(Px(1,2:3),'--',clx(1,2:3),'-',{0.1 100})
setoptions(h,'PhaseMatching','on')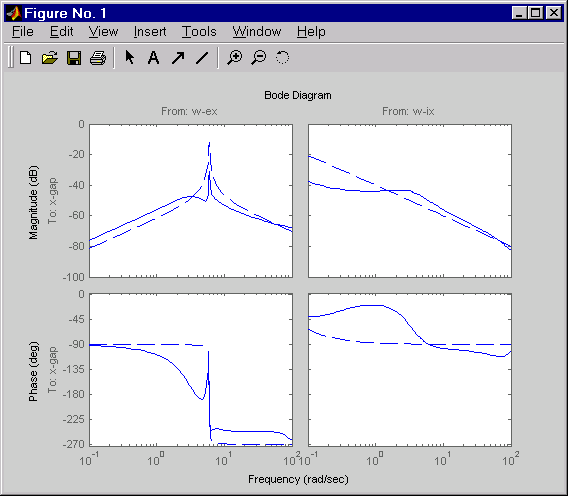

Пунктирные линии показывают ответ разомкнутого контура. Обратите внимание на то, что пиковое усиление ответа эксцентриситета к разрыву и низкочастотное усиление входной толщины, чтобы разорвать ответ уменьшались приблизительно на 20 дБ.

Наконец, используйте lsim симулировать открытое - и ответы времени с обратной связью на белый шум вводит _wex и _wix. Выберите dt=0.01 как шаг расчета для симуляции, и выводят эквивалентные дискретные белые шумовые входные параметры для этой частоты дискретизации.

dt = 0.01
t = 0:dt:50   % time samples

% Generate unit-covariance driving noise wx = [w-ex;w-ix].
% Equivalent discrete covariance is 1/dt
wx = sqrt(1/dt) * randn(2,length(t))

lsim(Px(1,2:3),':',clx(1,2:3),'-',wx,t)

Щелкните правой кнопкой по графику, который появляется, и выберите Show Input, чтобы выключить отображение входа.

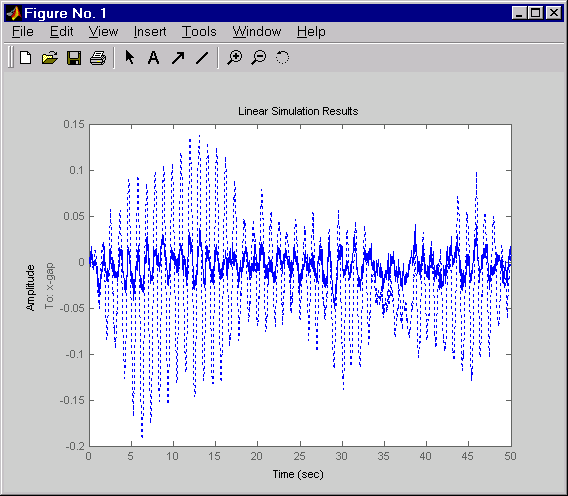
Пунктирные линии соответствуют ответу разомкнутого контура. В этой симуляции регулирование LQG уменьшает пиковое изменение толщины фактором 4.

Проект LQG для оси Y

Проект LQG для y - ось (регулирование толщины y) выполняет те же самые шаги что касается x - ось.

% Specify model components
Hy = tf(7.8e8,[1 71 88^2],'inputn','u-y') 
Fiy = tf(2e4,[1 0.05],'inputn','w-iy') 
Fey = tf([1e5 0],[1 0.19 9.4^2],'inputn','w-ey')
gy = 0.5e-6 % force-to-gap gain

% Build open-loop model
Py = append([ss(Hy) Fey],Fiy)
Py = [-gy gy;1 1] * Py
set(Py,'outputn',{'y-gap' 'y-force'})

% State-feedback gain design
Pydes = append(lpf,1) * Py % Add low-freq. weigthing
set(Pydes,'outputn',{'y-gap*' 'y-force'})
ky = lqry(Pydes(1,1),1,1e-4)

% Kalman estimator design
esty = kalman(Pydes(2,:),eye(2),1e3)

% Form SISO LQG regulator for y-axis and close the loop
Regy = lqgreg(esty,ky)
cly = feedback(Py,Regy,1,2,+1)

Сравните открытое - и ответ с обратной связью на белые шумовые входные воздействия.

dt = 0.01
t = 0:dt:50
wy = sqrt(1/dt) * randn(2,length(t))

lsim(Py(1,2:3),':',cly(1,2:3),'-',wy,t)

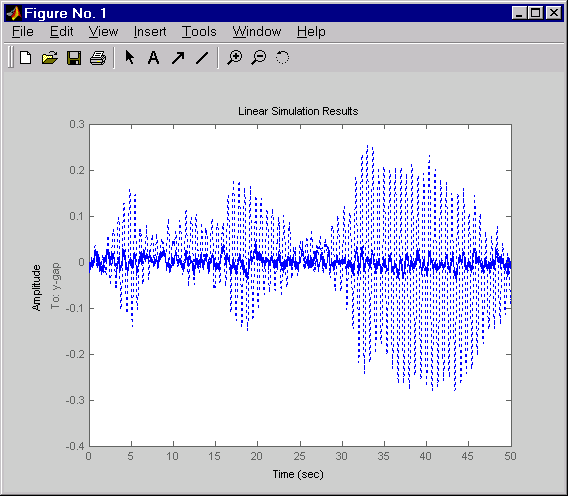
Пунктирные линии соответствуют ответу разомкнутого контура. Результаты симуляции сопоставимы с теми для x - ось.

Перекрестная связь между осями

x/y регулирование толщины, проблема MIMO. До сих пор вы обработали каждую ось отдельно и замкнули один круг SISO за один раз. Этот проект допустим целый, эти две оси справедливо разъединяются. К сожалению, этот процесс металлопрокатного завода показывает определенную степень перекрестной связи между осями. Физически, увеличение гидравлической силы вдоль x - ось сжимает материал, который в свою очередь повышает силу отпора на y - цилиндры оси. Результатом является увеличение y - толщины и эквивалентного (относительного) уменьшения в гидравлической силе вдоль y - ось.

Фигура ниже показов связь.

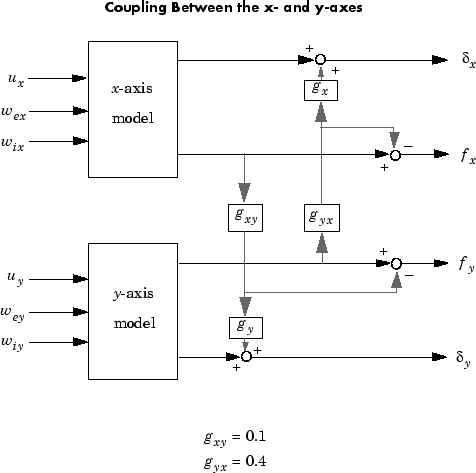
Соответственно, разрывы толщины и прокручивающиеся силы связаны с выходными параметрами ${\bar{δ}}_{x}, {\bar{f}}_{x}, \dots$ из x - и y - модели оси

$[\begin{array}{l} δ_{x} \\ δ_{y} \\ f_{x} \\ f_{x} \end{array}] = \underset{матрица перекрестной связи}{\underset{︸}{[\begin{matrix} 1 & 0 & 0 & g_{y x} g_{x} \\ 0 & 1 & g_{x y} g_{y} & 0 \\ 0 & 0 & 1 & - g_{y x} \\ 0 & 0 & - g_{x y} & 1 \end{matrix}]}} [\begin{array}{l} {\bar{δ}}_{x} \\ {\bar{δ}}_{y} \\ {\bar{f}}_{x} \\ {\bar{f}}_{y} \end{array}]$

Давайте смотреть, как предыдущее "разъединило" тарифы проекта LQG, когда перекрестная связь учтена. Чтобы создать модель 2D осей, показанную выше, добавляют модели Px и Py для x - и y - оси.

P = append(Px,Py)

Для удобства переупорядочьте вводы и выводы так, чтобы команды и разрывы толщины появились первыми.

P = P([1 3 2 4],[1 4 2 3 5 6])
P.outputname

ans = 
    'x-gap'
    'y-gap'
    'x-force'
    'y-force'

Наконец, поместите матрицу перекрестной связи последовательно с выходными параметрами.

gxy = 0.1; gyx = 0.4;
CCmat = [eye(2) [0 gyx*gx;gxy*gy 0] ; zeros(2) [1 -gyx;-gxy 1]]
Pc = CCmat * P
Pc.outputname = P.outputname

Чтобы симулировать ответ с обратной связью, также сформируйте модель с обратной связью

feedin = 1:2 % first two inputs of Pc are the commands
feedout = 3:4 % last two outputs of Pc are the measurements
cl = feedback(Pc,append(Regx,Regy),feedin,feedout,+1)

Вы теперь готовы симулировать открытое - и ответы с обратной связью на ведущие белые шумы wx (для x - ось) и wy (для y - ось).

wxy = [wx ; wy]
lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)

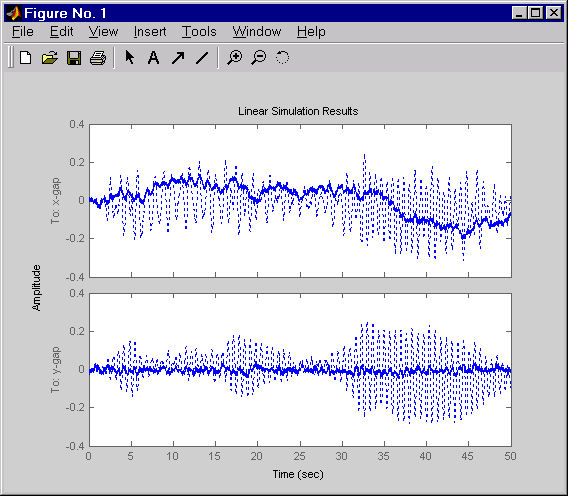
Ответ показывает серьезное ухудшение в эффективности регулирования вдоль x - ось (пиковое изменение толщины приблизительно в четыре раза больше, чем в симуляции без перекрестной связи). Следовательно, разработка для одного цикла за один раз является несоответствующей для этого уровня перекрестной связи, и необходимо выполнить объединенную ось проект MIMO, чтобы правильно обработать связывающиеся эффекты.

Проект MIMO LQG

Начните с полной модели в пространстве состояний 2D оси Pc выведенный в Перекрестной связи Между Осями. Входы и выходы модели

Pc.inputname

ans = 
    'u-x'
    'u-y'
    'w-ex'
    'w-ix'
    'w_ey'
    'w_iy'

P.outputname

ans = 
    'x-gap'
    'y-gap'
    'x-force'
    'y-force'

Как ранее, добавьте фильтры lowpass последовательно с 'x-gap' и 'y-gap' выходные параметры, чтобы оштрафовать только низкочастотные изменения толщины.

Pdes = append(lpf,lpf,eye(2)) * Pc
Pdes.outputn = Pc.outputn

Затем спроектируйте усиление LQ и утвердите средство оценки как прежде (существует теперь две команды и два измерения).

k = lqry(Pdes(1:2,1:2),eye(2),1e-4*eye(2))      % LQ gain
est = kalman(Pdes(3:4,:),eye(4),1e3*eye(2))     % Kalman estimator

RegMIMO = lqgreg(est,k)      % form MIMO LQG regulator

Получившийся регулятор LQG RegMIMO имеет два входных параметров и два выходных параметров.

RegMIMO.inputname

ans = 
    'x-force'
    'y-force'

RegMIMO.outputname

ans = 
    'u-x'
    'u-y'

Постройте его ответ сингулярного значения (основные усиления).

sigma(RegMIMO)

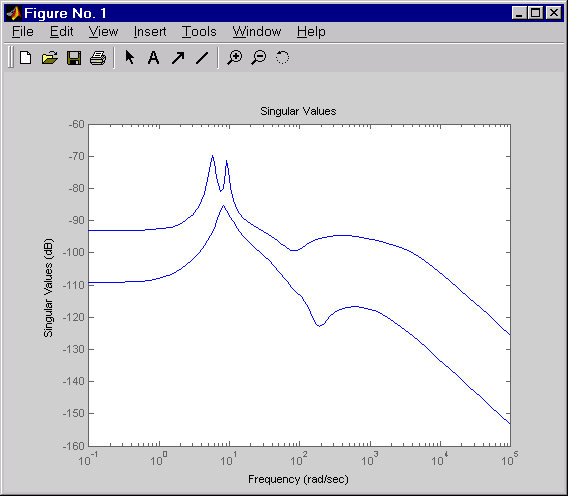
Затем постройте открытое - и ответы времени с обратной связью на белые шумовые входные параметры (использующий регулятор MIMO LQG для обратной связи).

% Form the closed-loop model
cl = feedback(Pc,RegMIMO,1:2,3:4,+1);

% Simulate with lsim using same noise inputs
lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)

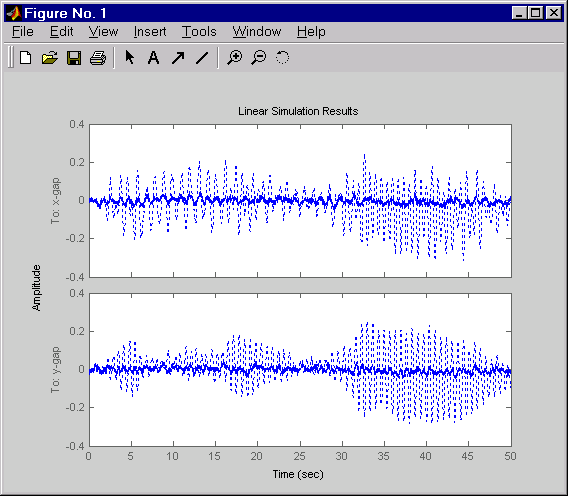
Проект MIMO является ясным улучшением по сравнению с отдельными проектами SISO для каждой оси. В частности, уровень x/y изменение толщины теперь сопоставим с полученным в разъединенном случае. Этот пример иллюстрирует преимущества прямого проекта MIMO для многомерных систем.

Ссылки

[1] Grimble, M.J., Устойчивое Управление производственным процессом: Оптимальный Подход Проекта для Полиномиальных Систем, Prentice Hall, 1994, p. 261 и стр 443-456.

Документация