Рациональные модели заданы как отношения полиномов и даны
где n является степенью полинома числителя и 0 ≤ n ≤ 5, в то время как m является степенью полинома знаменателя и 1 ≤ m ≤ 5. Обратите внимание на то, что коэффициент, сопоставленный с xm всегда, равняется 1. Это делает числитель и знаменатель уникальными, когда полиномиальные степени являются тем же самым.
В этом руководстве rationals описаны в терминах степени степени числителя / знаменателя. Например, квадратичным/кубическим рациональным уравнением дают
Как полиномы, часто используются rationals, когда простая эмпирическая модель требуется. Основным преимуществом rationals является их гибкость с данными, которые имеют сложную структуру. Основной недостаток - то, что они становятся нестабильными, когда знаменатель - приблизительно 0. Для примера, который использует рациональные полиномы различных степеней, смотрите Пример: Рациональная Подгонка.
Откройте приложение Curve Fitting путем ввода cftool. В качестве альтернативы нажмите Curve Fitting на вкладке Apps.
В приложении Curve Fitting выберите данные о кривой (X data и Y data, или только Y data против индекса).
Приложение Curve Fitting создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели от Polynomial к Rational.
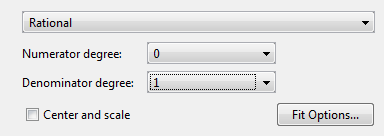
Можно задать следующие опции:
Выберите степень полинома числителя и полинома знаменателя. Числитель может иметь степень 0 к 5, и знаменатель от 1 к 5.
Посмотрите в панели Results, чтобы видеть условия модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Нажмите Fit Options, чтобы задать содействующие начальные значения и ограничительные границы, или изменить настройки алгоритма.
Тулбокс вычисляет случайные стартовые точки для рациональных моделей, заданных на интервале [0,1]. Можно заменить стартовые точки и задать собственные значения в Подходящем Окне параметров.
Для получения дополнительной информации о настройках см. Опции Подгонки Определения и Оптимизированные Начальные точки.
Задайте тип модели ratij, где i является степенью полинома числителя, и j является степенью полинома знаменателя. Например, 'rat02', 'rat21' или 'rat55'.
Например, чтобы загрузить некоторые данные и подбирать рациональную модель:
load hahn1; f = fit( temp, thermex, 'rat32') plot(f,temp,thermex)
Смотрите Пример: Рациональная Подгонка, чтобы соответствовать этому примеру в интерактивном режиме различными рациональными моделями.
Если вы хотите изменить подходящие опции, такие как содействующие начальные значения, и ограничительные границы, подходящие для ваших данных, или изменить настройки алгоритма, видят таблицу дополнительных свойств с NonlinearLeastSquares на fitoptions страница с описанием.
Этот пример соответствует результатам измерений с помощью рациональной модели. Данные описывают коэффициент теплового расширения для меди в зависимости от температуры в градусах кельвин.
Для этого набора данных вы найдете рациональное уравнение, которое производит лучшую подгонку. Рациональные модели заданы как отношение полиномов, как дано:
где n является степенью полинома числителя, и m является степенью полинома знаменателя. Обратите внимание на то, что рациональные уравнения не сопоставлены с физическими параметрами данных. Вместо этого они предоставляют простую и гибкую эмпирическую модель, которую можно использовать для интерполяции и экстраполяции.
Загрузите тепловые данные о расширении из файла hahn1.mat, которому предоставляют тулбокс.
load hahn1
Рабочая область содержит две новых переменные:
temp вектор из температур в градусах кельвин.
thermex вектор из тепловых коэффициентов расширения для меди.
Откройте приложение Curve Fitting путем ввода:
cftool
Выберите temp и thermex от X data и списков Y data.
Приложение Curve Fitting соответствует и отображает данные на графике.
Выберите Rational в подходящем списке категорий.
Попробуйте начальный выбор за рациональную модель квадратичных/квадратичных. Выберите 2 и для Numerator degree и для Denominator degree.
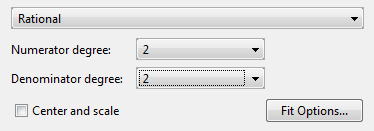
Приложение Curve Fitting соответствует квадратичному/квадратичному рациональному.
Исследуйте остаточные значения. Выберите View> Residuals Plot или нажмите кнопку на панели инструментов.
Исследуйте данные, подгонку и остаточные значения. Заметьте, что подгонка пропускает данные для наименьших и самых больших значений предиктора. Кроме того, остаточные значения показывают сильный шаблон в целом наборе данных, указывая, что лучшая подгонка возможна.
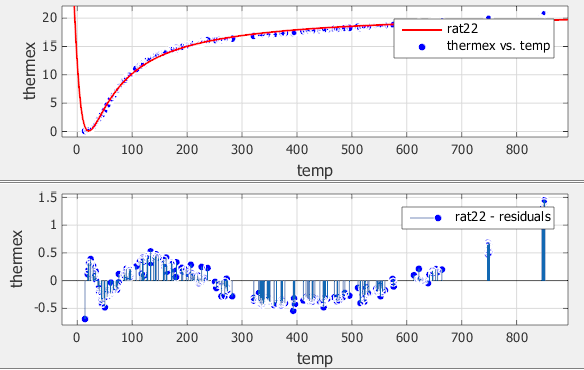
Для следующей подгонки попробуйте кубическое / кубическое уравнение. Выберите 3 и для Numerator degree и для Denominator degree.
Исследуйте данные, подгонку и остаточные значения. Подгонка показывает несколько разрывов вокруг нулей знаменателя.
Примечание
Ваши результаты зависят от случайных стартовых точек и могут варьироваться от показанных.
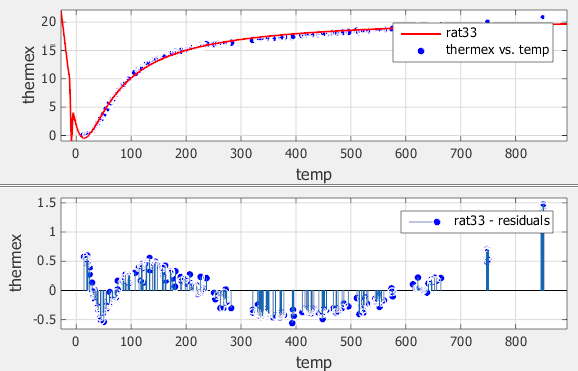
Посмотрите в панели Results. Сообщение и числовые результаты указывают, что подгонка не сходилась.
Fit computation did not converge: Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum.
Несмотря на то, что сообщение в панели Результатов указывает, что вы можете улучшить подгонку, если вы увеличиваете максимальное число итераций, лучший выбор на этом этапе подходящего процесса состоит в том, чтобы использовать различное рациональное уравнение, потому что текущая подгонка содержит несколько разрывов. Эти разрывы происходят из-за функции, аварийно завершающейся в значениях предиктора, которые соответствуют нулям знаменателя.
Попробуйте подгонку данных с помощью кубического / квадратного уравнения. Выберите 2 для Denominator degree и отпуска набор Numerator degree к 3.
Входные переменные имеют совсем другие шкалы, поэтому выберите опцию Center and scale.
Данные, подгонку и остаточные значения показывают ниже.
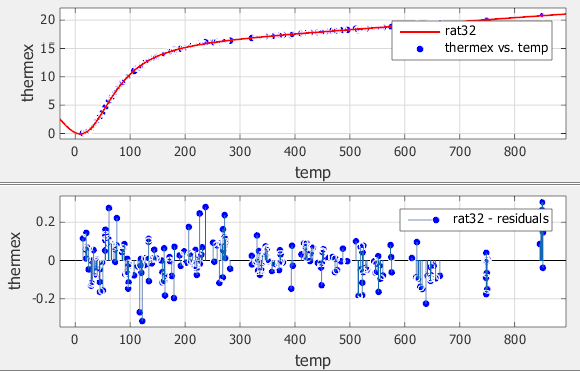
Подгонка хорошего поведения в целой области значений данных, и остаточные значения случайным образом рассеиваются о нуле. Поэтому можно уверенно использовать это подходящее для последующего анализа.
fit | fitoptions | fittype