Факторная квадратная Эрмитова положительная определенная матрица на треугольные компоненты
Математические функции / Матрицы и Линейная алгебра / Матричные Факторизации
dspfactors
Блок Cholesky Factorization исключительно учитывает квадратную Эрмитовую положительную определенную входную матрицу S как
где L является нижней треугольной квадратной матрицей с положительными диагональными элементами, и L* является Эрмитовым (сопряженное комплексное число), транспонируют L. Блок выводит матрицу с более низкими треугольными элементами от L и верхними треугольными элементами от L*. Выход не находится в той же форме как выход MATLAB®
chol функция. Для того, чтобы преобразовать выход блока Cholesky Factorization к форме MATLAB, используйте следующее уравнение:
R = triu(LL');
Для того, чтобы извлечь матрицу L исключительно, передайте выход блока Cholesky Factorization, LL', с блоком Extract Triangular Matrix. Установка параметра Extract Extract Triangular Matrix к Lower извлекает матрицу L. Установка параметра Extract на Upper извлекает матрицу L'.
Здесь, LL' выход блока Cholesky Factorization. Из-за ошибки округления, эти уравнения не приводят к результату, который является точно тем же самым как результатом MATLAB.
Блок Выход, составленный из L и L*
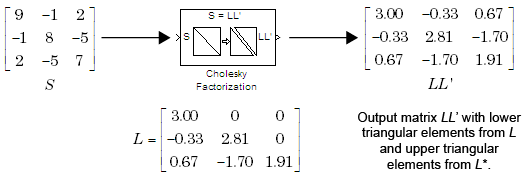
Блок выход допустим только, когда его вход имеет следующие характеристики:
Эрмитов — блок не проверяет, является ли вход Эрмитовым; это использует только диагональный и верхний треугольник входа, чтобы вычислить выход.
Диагональные элементы с действительным знаком — блок игнорирует любой мнимый компонент диагональных элементов входа.
Положительный определенный — Набор блок, чтобы уведомить вас, когда вход не положителен определенный как описано в Ответе на Неположительный Определенный Вход.
Чтобы сгенерировать допустимый выход, алгоритм блока требует положительного определенного входа (см. Входные Требования для Допустимого Выхода). Установите параметр Non-positive definite input, чтобы определить, как блок отвечает на неположительный определенный вход:
Ignore — Возобновите расчет и не выпускайте предупреждение. Выход не является допустимой факторизацией. Частичная факторизация будет присутствовать в левом верхнем углу выхода.
Warning — Отобразите предупреждающее сообщение в командном окне MATLAB и продолжите симуляцию. Выход не является допустимой факторизацией. Частичная факторизация будет присутствовать в левом верхнем углу выхода.
Error — Отобразите ошибочное диалоговое окно и отключите симуляцию.
Примечание
Параметр Non-positive definite input является диагностическим параметром. Как все диагностические параметры на диалоговом окне Configuration Parameters, это установлено в Ignore в коде, сгенерированном для этого блока программным обеспечением генерации кода Simulink® Coder™.
Обратите внимание на то, что L и L* совместно используют ту же диагональ в выходной матрице. Факторизация Холесского требует половины расчета Исключения Гаусса (LU-разложение) и всегда устойчива.
Ответ на неположительные определенные матричные входные параметры: IgnoreПредупреждение, или Error. Смотрите ответ на неположительный определенный вход.
Golub, G. H. и К. Ф. ван Лоун. Матричные Расчеты. 3-й редактор Балтимор, MD: Johns Hopkins University Press, 1996.
| Порт | Поддерживаемые типы данных |
|---|---|
S |
|
LL |
|
| Autocorrelation LPC | DSP System Toolbox |
| Cholesky Inverse | DSP System Toolbox |
| Cholesky Solver | DSP System Toolbox |
| LDL Factorization | DSP System Toolbox |
| LU Factorization | DSP System Toolbox |
| QR Factorization | DSP System Toolbox |
| MATLAB |
Смотрите Матричные Факторизации для сопутствующей информации.