Создайте модели регрессии с ошибками ARMA

Модель регрессии по умолчанию с ошибками ARMA

В этом примере показано, как применить краткий regARIMA(p,D,q) синтаксис, чтобы задать модель регрессии с ошибками ARMA.

Задайте модель регрессии по умолчанию с ARMA (3,2) ошибки:

$\begin{array}{l} y_{t} = c + X_{t} β + u_{t} \\ u_{t} = a_{1} u_{t - 1} + a_{2} u_{t - 2} + a_{3} u_{t - 3} + ε_{t} + b_{1} ε_{t - 1} + b_{2} ε_{t - 2} . \end{array}$

Mdl = regARIMA(3,0,2)

Mdl = 
  regARIMA with properties:

     Description: "ARMA(3,2) Error Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
       Intercept: NaN
            Beta: [1×0]
               P: 3
               Q: 2
              AR: {NaN NaN NaN} at lags [1 2 3]
             SAR: {}
              MA: {NaN NaN} at lags [1 2]
             SMA: {}
        Variance: NaN

Программное обеспечение устанавливает каждый параметр на NaN, и инновационное распределение к Gaussian. Коэффициенты AR в задержках 1 - 3, и коэффициенты MA в задержках 1 и 2.

Передайте Mdl в estimate с данными, чтобы оценить набор параметров к NaN. regARIMA модель устанавливает Beta к [] и не отображает его. Если вы передаете матрицу предикторов ( $X_{t}$ ) в estimate, затем estimate оценки Beta. estimate функция выводит количество коэффициентов регрессии в Beta от количества столбцов в $X_{t}$ .

Задачи, такие как симуляция и предсказывающий использование simulate и forecast не принимайте модели по крайней мере с одним NaN для значения параметров. Используйте запись через точку, чтобы изменить значения параметров.

Ошибочная модель ARMA без точки пересечения

Скрипт Open Live Script

В этом примере показано, как задать модель регрессии с ошибками ARMA без точки пересечения регрессии.

Задайте модель регрессии по умолчанию с ARMA (3,2) ошибки:

$\begin{array}{l} y_{t} = X_{t} β + u_{t} \\ u_{t} = a_{1} u_{t - 1} + a_{2} u_{t - 2} + a_{3} u_{t - 3} + ε_{t} + b_{1} ε_{t - 1} + b_{2} ε_{t - 2} . \end{array}$

Mdl = regARIMA('ARLags',1:3,'MALags',1:2,'Intercept',0)

Mdl = 
  regARIMA with properties:

     Description: "ARMA(3,2) Error Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
       Intercept: 0
            Beta: [1×0]
               P: 3
               Q: 2
              AR: {NaN NaN NaN} at lags [1 2 3]
             SAR: {}
              MA: {NaN NaN} at lags [1 2]
             SMA: {}
        Variance: NaN

Программное обеспечение устанавливает Intercept к 0, но все другие параметры в Mdl NaN значения по умолчанию.

Начиная с Intercept не NaN, это - ограничение равенства во время оценки. Другими словами, если вы передаете Mdl и данные в estimate, затем estimate наборы Intercept к 0 во время оценки.

Можно изменить свойства Mdl использование записи через точку.

Ошибочная модель ARMA с непоследовательными задержками

Скрипт Open Live Script

В этом примере показано, как задать модель регрессии с ошибками ARMA, где ненулевые условия ARMA в непоследовательных задержках.

Задайте модель регрессии с ARMA (8,4) ошибки:

$\begin{array}{l} y_{t} = c + X_{t} β + u_{t} \\ u_{t} = a_{1} u_{1} + a_{4} u_{4} + a_{8} u_{8} + ε_{t} + b_{1} ε_{t - 1} + b_{4} ε_{t - 4} . \end{array}$

Mdl = regARIMA('ARLags',[1,4,8],'MALags',[1,4])

Mdl = 
  regARIMA with properties:

     Description: "ARMA(8,4) Error Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
       Intercept: NaN
            Beta: [1×0]
               P: 8
               Q: 4
              AR: {NaN NaN NaN} at lags [1 4 8]
             SAR: {}
              MA: {NaN NaN} at lags [1 4]
             SMA: {}
        Variance: NaN

Коэффициенты AR в задержках 1, 4, и 8, и коэффициенты MA в задержках 1 и 4. Программное обеспечение устанавливает временные задержки на 0.

Передайте Mdl и данные в estimate. Программное обеспечение оценивает все параметры, которые имеют значение NaN. Затем estimate содержит все временные коэффициенты задержки к 0 во время оценки.

Известные значения параметров для модели регрессии с ошибками ARMA

Скрипт Open Live Script

В этом примере показано, как задать значения для всех параметров модели регрессии с ошибками ARMA.

Задайте модель регрессии с ARMA (3,2) ошибки:

$\begin{array}{l} y_{t} = X_{t} [\begin{array}{l} 2.5 \\ - 0.6 \end{array}] + u_{t} \\ u_{t} = 0.7 u_{t - 1} - 0.3 u_{t - 2} + 0.1 u_{t - 3} + ε_{t} + 0.5 ε_{t - 1} + 0.2 ε_{t - 2}, \end{array}$

где $ε_{t}$ является Гауссовым с модульным отклонением.

Mdl = regARIMA('Intercept',0,'Beta',[2.5; -0.6],...
    'AR',{0.7, -0.3, 0.1},'MA',{0.5, 0.2},'Variance',1)

Mdl = 
  regARIMA with properties:

     Description: "Regression with ARMA(3,2) Error Model (Gaussian Distribution)"
    Distribution: Name = "Gaussian"
       Intercept: 0
            Beta: [2.5 -0.6]
               P: 3
               Q: 2
              AR: {0.7 -0.3 0.1} at lags [1 2 3]
             SAR: {}
              MA: {0.5 0.2} at lags [1 2]
             SMA: {}
        Variance: 1

Параметры в Mdl не содержите NaN значения, и поэтому нет никакой потребности оценить Mdl использование estimate. Однако можно симулировать или предсказать ответы от Mdl использование simulate или forecast.

Модель регрессии с Ошибками ARMA и t Инновациями

Скрипт Open Live Script

В этом примере показано, как установить инновационное распределение модели регрессии с ошибками ARMA к t распределению.

Задайте модель регрессии с ARMA (3,2) ошибки:

$\begin{array}{l} y_{t} = X_{t} [\begin{array}{l} 2.5 \\ - 0.6 \end{array}] + u_{t} \\ u_{t} = 0.7 u_{t - 1} - 0.3 u_{t - 2} + 0.1 u_{t - 3} + ε_{t} + 0.5 ε_{t - 1} + 0.2 ε_{t - 2}, \end{array}$

где $ε_{t}$ имеет t распределение со степенями свободы по умолчанию и модульным отклонением.

Mdl = regARIMA('Intercept',0,'Beta',[2.5; -0.6],...
    'AR',{0.7, -0.3, 0.1},'MA',{0.5, 0.2},'Variance',1,...
    'Distribution','t')

Mdl = 
  regARIMA with properties:

     Description: "Regression with ARMA(3,2) Error Model (t Distribution)"
    Distribution: Name = "t", DoF = NaN
       Intercept: 0
            Beta: [2.5 -0.6]
               P: 3
               Q: 2
              AR: {0.7 -0.3 0.1} at lags [1 2 3]
             SAR: {}
              MA: {0.5 0.2} at lags [1 2]
             SMA: {}
        Variance: 1

Степенями свободы по умолчанию является NaN. Если вы не знаете степеней свободы, то можно оценить его путем передачи Mdl и данные к estimate.

Задайте a $t_{5}$ распределение.

Mdl.Distribution = struct('Name','t','DoF',5)

Mdl = 
  regARIMA with properties:

     Description: "Regression with ARMA(3,2) Error Model (t Distribution)"
    Distribution: Name = "t", DoF = 5
       Intercept: 0
            Beta: [2.5 -0.6]
               P: 3
               Q: 2
              AR: {0.7 -0.3 0.1} at lags [1 2 3]
             SAR: {}
              MA: {0.5 0.2} at lags [1 2]
             SMA: {}
        Variance: 1

Можно симулировать или предсказать ответы от Mdl использование simulate или forecast потому что Mdl полностью задан.

В приложениях, таких как симуляция, программное обеспечение нормирует случайные t инновации. Другими словами, Variance заменяет теоретическое отклонение t случайной переменной (который является DoF/ (DoF - 2)), но консервы эксцесс распределения.

Задайте модель регрессии с ошибками ARMA приложение Econometric Modeler

В приложении Econometric Modeler можно задать переменные предикторы в компоненте регрессии, и ошибочную структуру задержки модели и инновационное распределение модели регрессии с ARMA (p, q) ошибки, путем выполнения этих шагов. Все заданные коэффициенты являются неизвестными но допускающими оценку параметрами.

В командной строке откройте приложение Econometric Modeler.
```
econometricModeler
```
В качестве альтернативы откройте приложение из галереи Apps (см. Econometric Modeler).
В панели Time Series выберите ряд времени отклика, к которому модель будет подходящей.
На вкладке Econometric Modeler, в разделе Models, кликают по стреле, чтобы отобразить галерею моделей.
В галерее моделей, в разделе Regression Models, нажимают RegARMA.
Диалоговое окно RegARMA Model Parameters появляется.
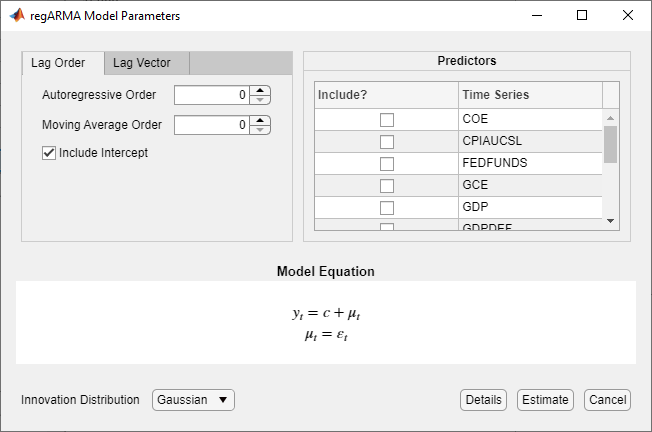
Выберите ошибочную структуру задержки модели. Чтобы задать модель регрессии с ARMA (p, q), ошибки, который включает все задержки AR от 1 до p и всех задержек MA от 1 до q, используют вкладку Lag Order. Для гибкости, чтобы задать включение особых задержек, используйте вкладку Lag Vector. Для получения дополнительной информации смотрите Полиномы Оператора Задержки Определения В интерактивном режиме. Независимо от вкладки вы используете, можно проверить форму модели путем осмотра уравнения в разделе Model Equation .
В разделе Predictors выберите по крайней мере один переменный предиктор путем установки флажка Include? для временных рядов.

Например, предположите, что вы работаете с Data_USEconModel.mat набор данных и его переменные перечислены в панели Time Series.

Задавать модель регрессии с AR (3) ошибки для уровня безработицы, содержащего весь последовательный AR, отстает от 1 до его порядка, Распределенных гауссовым образом инноваций и переменных предикторов COE, CPIAUCSL, FEDFUNDS и GDP:
1. В панели Time Series выберите UNRATE временные ряды.
2. На вкладке Econometric Modeler, в разделе Models, кликают по стреле, чтобы отобразить галерею моделей.
3. В галерее моделей, в разделе Regression Models, нажимают RegARMA.
  .
4. В диалоговом окне regARMA Model Parameters, на вкладке Lag Order, устанавливает Autoregressive Order на 3.
5. В разделе Predictors установите флажок Include? для COE, CPIAUCSL, FEDFUNDS и временных рядов GDP.
Задавать модель регрессии с MA (2) ошибки для уровня безработицы, содержащего весь MA, отстает от 1 до его порядка, Распределенных гауссовым образом инноваций и переменных предикторов COE и CPIAUCSL.
1. В панели Time Series выберите UNRATE временные ряды.
2. На вкладке Econometric Modeler, в разделе Models, кликают по стреле, чтобы отобразить галерею моделей.
3. В галерее моделей, в разделе Regression Models, нажимают RegARMA.
4. В диалоговом окне regARMA Model Parameters, на вкладке Lag Order, устанавливает Moving Average Order на 2.
5. В разделе Predictors установите флажок Include? для временных рядов CPIAUCSL и COE.
Задавать модель регрессии с ARMA (8,4) ошибки для уровня безработицы, содержащего непоследовательные задержки
$\begin{matrix} y_{t} = c + β_{1} C O E_{t} + β_{2} C P I A U C S L_{t} + u_{t} \\ (1 - α_{1} L - α_{4} L^{4} - α_{8} L^{8}) u_{t} = (1 + b_{1} L + b_{4} L^{4}) ε_{t} \end{matrix},$
где _εt является серией Гауссовых инноваций IID:
1. В панели Time Series выберите UNRATE временные ряды.
2. На вкладке Econometric Modeler, в разделе Models, кликают по стреле, чтобы отобразить галерею моделей.
3. В галерее моделей, в разделе Regression Models, нажимают RegARMA.
4. В диалоговом окне regARMA Model Parameters кликните по вкладке Lag Vector:
  1. В поле Autoregressive Lags введите 1 4 8.
  2. В поле Moving Average Lags введите 1 4.
5. В разделе Predictors установите флажок Include? для временных рядов CPIAUCSL и COE.
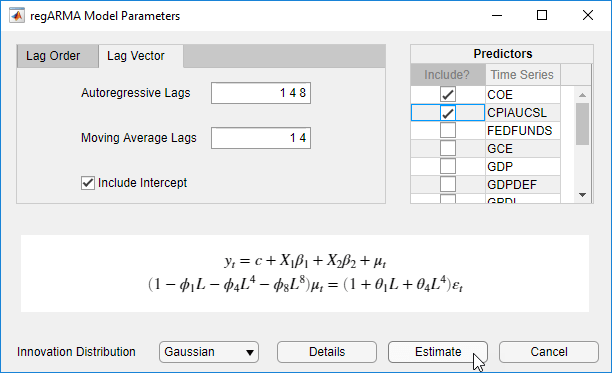
Задавать модель регрессии с ARMA (3,2) ошибки для уровня безработицы, содержащего весь последовательный AR и MA, отстает через их соответствующие порядки, переменные предикторы COE и CPIAUCSL и t - распределенные инновации:
1. В панели Time Series выберите UNRATE временные ряды.
2. На вкладке Econometric Modeler, в разделе Models, кликают по стреле, чтобы отобразить галерею моделей.
3. В галерее моделей, в разделе Regression Models, нажимают RegARMA.
4. В диалоговом окне regARMA Model Parameters кликните по вкладке Lag Order:
  1. Установите Autoregressive Order на 3.
  2. Установите Moving Average Order на 2.
5. Нажмите кнопку Innovation Distribution, затем выберите t.
6. В разделе Predictors установите флажок Include? для временных рядов CPIAUCSL и COE.
Параметр степеней свободы распределения t является неизвестным, но допускающим оценку параметром.

После того, как вы зададите модель, нажмите Estimate, чтобы оценить все неизвестные параметры в модели.

Смотрите также

Связанные примеры

Больше о

Модели регрессии с ошибками временных рядов

Документация