То В этом примере показано, как использовать два различных метода, чтобы калибровать стохастическую модель энергозависимости SABR с рынка, подразумевало Черные колебания. Оба использования подходов blackvolbysabr.
Загрузите рынок подразумеваемые черные данные об энергозависимости
Метод 2: калибруйте ро и ню допущением альфы от энергозависимости в деньгах
То В этом примере показано, как создать гипотетический рынок, подразумевало Черные колебания для европейского swaptions в области значений забастовок перед калибровкой. swaptions истекают за три года от Settle дата и имеет 10-летние подкачки как базовый инструмент. Уровни описываются в десятичных числах. (Изменение модулей влияет на численное значение и интерпретацию Alpha введите параметр к функциональному blackvolbysabr.)
Загрузите подразумеваемые Черные данные об энергозависимости рынка для swaptions, истекающего за три года.
Settle = '12-Jun-2013'; ExerciseDate = '12-Jun-2016'; MarketStrikes = [2.0 2.5 3.0 3.5 4.0 4.5 5.0]'/100; MarketVolatilities = [45.6 41.6 37.9 36.6 37.8 39.2 40.0]'/100;
Во время Settle, задайте базовый форвардный курс и энергозависимость в деньгах.
CurrentForwardValue = MarketStrikes(4) ATMVolatility = MarketVolatilities(4)
CurrentForwardValue =
0.0350
ATMVolatility =
0.3660В этом примере показано, как калибровать the Alpha\rho, и Nu введите параметры непосредственно. Значение Beta предопределяется или путем подбора кривой историческим данным о волатильности рынка или путем выбора значения, которое считают подходящим для того рынка [1].
Задайте предопределенный Beta.
Beta1 = 0.5;
После фиксации значения \beta), параметры \alpha), \rho), и \nu) все адаптированы непосредственно. Функция Optimization Toolbox™ lsqnonlin генерирует значения параметров, которые минимизируют квадратичную невязку между волатильностью рынка и колебаниями, вычисленными blackvolbysabr.
% Calibrate Alpha, Rho, and Nu objFun = @(X) MarketVolatilities - ... blackvolbysabr(X(1), Beta1, X(2), X(3), Settle, ... ExerciseDate, CurrentForwardValue, MarketStrikes); X = lsqnonlin(objFun, [0.5 0 0.5], [0 -1 0], [Inf 1 Inf]); Alpha1 = X(1); Rho1 = X(2); Nu1 = X(3);
Local minimum possible. lsqnonlin stopped because the final change in the sum of squares relative to its initial value is less than the default value of the function tolerance.
В этом примере показано, как использовать альтернативный калибровочный метод где значение \beta) снова предопределяется как в Методе 1.
Задайте предопределенный Beta.
Beta2 = 0.5;
Однако после фиксации значения \beta), параметры \rho), и \nu) адаптированы непосредственно в то время как \alpha) подразумевается с рынка энергозависимость в деньгах. Калиброванное использование моделей этого метода производит колебания в деньгах, которые равны рыночным котировкам. Этот подход широко используется в swaptions, где колебания в деньгах заключаются в кавычки наиболее часто и важны для соответствия. Подразумевать \alpha) с рынка энергозависимость в деньгах (), следующий кубический полином решен для \alpha), и самый маленький положительный действительный корень выбран [2].
где:
текущее прямое значение.
часть года к зрелости.
Чтобы выполнить это, задайте анонимную функцию как:
% Year fraction from Settle to option maturity T = yearfrac(Settle, ExerciseDate, 1); % This function solves the SABR at-the-money volatility equation as a % polynomial of Alpha alpharoots = @(Rho,Nu) roots([... (1 - Beta2)^2*T/24/CurrentForwardValue^(2 - 2*Beta2) ... Rho*Beta2*Nu*T/4/CurrentForwardValue^(1 - Beta2) ... (1 + (2 - 3*Rho^2)*Nu^2*T/24) ... -ATMVolatility*CurrentForwardValue^(1 - Beta2)]); % This function converts at-the-money volatility into Alpha by picking the % smallest positive real root atmVol2SabrAlpha = @(Rho,Nu) min(real(arrayfun(@(x) ... x*(x>0) + realmax*(x<0 || abs(imag(x))>1e-6), alpharoots(Rho,Nu))));
Функциональный atmVol2SabrAlpha преобразует энергозависимость в деньгах в \alpha) для данного набора \rho) и \nu). Эта функция затем используется в целевой функции, чтобы соответствовать параметрам \rho) и \nu).
% Calibrate Rho and Nu (while converting at-the-money volatility into Alpha % using atmVol2SabrAlpha) objFun = @(X) MarketVolatilities - ... blackvolbysabr(atmVol2SabrAlpha(X(1), X(2)), ... Beta2, X(1), X(2), Settle, ExerciseDate, CurrentForwardValue, ... MarketStrikes); X = lsqnonlin(objFun, [0 0.5], [-1 0], [1 Inf]); Rho2 = X(1); Nu2 = X(2);
Local minimum found. Optimization completed because the size of the gradient is less than the default value of the function tolerance.
Калиброванный параметр \alpha) вычисляется с помощью калиброванных параметров \rho) и \nu).
% Obtain final Alpha from at-the-money volatility using calibrated parameters Alpha2 = atmVol2SabrAlpha(Rho2, Nu2); % Display calibrated parameters C = {Alpha1 Beta1 Rho1 Nu1;Alpha2 Beta2 Rho2 Nu2}; CalibratedPrameters = cell2table(C,... 'VariableNames',{'Alpha' 'Beta' 'Rho' 'Nu'},... 'RowNames',{'Method 1';'Method 2'})
CalibratedPrameters =
Alpha Beta Rho Nu
________ ____ _______ _______
Method 1 0.060277 0.5 0.2097 0.75091
Method 2 0.058484 0.5 0.20568 0.79647
В этом примере показано, как использовать калиброванные модели, чтобы вычислить новые колебания в любом значении забастовки.
Вычислите колебания для моделей, калиброванных с помощью Метода 1 и Метода 2, и постройте результаты.
PlottingStrikes = (1.75:0.1:5.50)'/100; % Compute volatilities for model calibrated by Method 1 ComputedVols1 = blackvolbysabr(Alpha1, Beta1, Rho1, Nu1, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); % Compute volatilities for model calibrated by Method 2 ComputedVols2 = blackvolbysabr(Alpha2, Beta2, Rho2, Nu2, Settle, ... ExerciseDate, CurrentForwardValue, PlottingStrikes); figure; plot(MarketStrikes,MarketVolatilities,'xk',... PlottingStrikes,ComputedVols1,'b', ... PlottingStrikes,ComputedVols2,'r', ... CurrentForwardValue,ATMVolatility,'ok',... 'MarkerSize',10); xlim([0.01 0.06]); ylim([0.35 0.5]); xlabel('Strike', 'FontWeight', 'bold'); ylabel('Implied Black Volatility', 'FontWeight', 'bold'); legend('Market Volatilities', 'SABR Model (Method 1)',... 'SABR Model (Method 2)', 'At-the-money volatility');
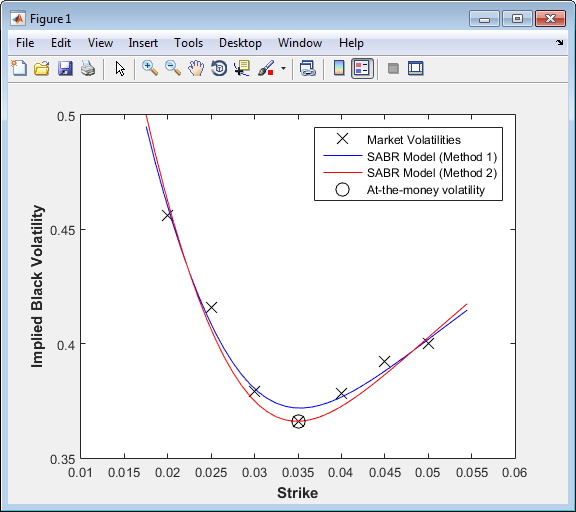
Модель, калиброванная с помощью Метода 2, воспроизводит рынок энергозависимость в деньгах (отмеченный кругом) точно.
[1] Хейган, P. S. Кумар, D., Лесниевский, A. S. и Лесничий, Д. Э., Управляя риском улыбки, Журналом Wilmott, 2002.
[2] Запад, G., “Калибровка Модели SABR на Неликвидных Рынках”, Прикладные Математические Финансы, 12 (4), стр 371–385, 2004.
blackvolbysabr | optsensbysabr | swaptionbyblk