Числа фиксированной точки ограничиваются, в котором они не могут одновременно представлять очень большие или очень небольшие числа с помощью разумного размера слова. Это ограничение может быть преодолено при помощи экспоненциального представления. С экспоненциальным представлением можно динамически поместить двоичную точку в удобном местоположении и использовать степени двоичного файла отслеживать то местоположение. Таким образом можно представлять область значений очень больших и очень небольших чисел только с несколькими цифрами.
Можно представлять любое бинарное число с плавающей запятой в форме экспоненциального представления как f 2e, где f является частью (или мантисса), 2 основание или основа (двоичный файл в этом случае), и e является экспонентой основания. Основание является всегда положительным числом, в то время как f и e могут быть положительными или отрицательными.
При выполнении арифметических операций оборудование с плавающей точкой должно учесть, что знак, экспонента и часть все закодированы в том же двоичном слове. Это приводит к схемам сложной логики при сравнении со схемами для бинарных операций фиксированной точки.
Программное обеспечение Fixed-Point Designer™ поддерживает полуточность, и числа с плавающей запятой с двойной точностью с одинарной точностью, как задано IEEE® Standard 754.
Прямая аналогия существует между обозначением экспоненциального представления и разделительной точки. Например, экспоненциальное представление с помощью пяти десятичных цифр для части приняло бы форму
где и p является целым числом неограниченной области значений.
Обозначение разделительной точки с помощью пяти битов для части является тем же самым за исключением основания системы счисления
где и q является целым числом неограниченной области значений.
Для чисел фиксированной точки фиксируется экспонента, но нет никакой причины, почему двоичная точка должна быть непрерывной с частью. Для получения дополнительной информации смотрите Интерпретацию Двоичной точки.
Стандарт IEEE 754 был широко принят и используется с фактически всеми процессорами с плавающей точкой и арифметическими сопроцессорами с существенным исключением многих DSP процессоры с плавающей точкой.
Этот стандарт задает несколько форматов числа с плавающей запятой, из которых одиночных игр и удваивается, наиболее широко используется. Каждый формат содержит три компонента: знаковый бит, дробное поле и поле экспоненты.
Числа с плавающей запятой IEEE используют представление знака/величины, где знаковый бит явным образом включен в слово. Используя представление знака/величины, знаковый бит 0 представляет положительное число, и знаковый бит 1 представляет отрицательное число. Это в отличие от дополнительного представления two, предпочтенного для чисел фиксированной точки со знаком.
Числа с плавающей запятой могут быть представлены многими различными способами путем сдвига номера налево или направо от двоичной точки и уменьшения или увеличения экспоненты двоичного файла соответствующей суммой.
Чтобы упростить операции на числах с плавающей запятой, они нормированы в формате IEEE. Нормированное двоичное число имеет часть формы 1. f, где f имеет фиксированный размер для типа определенных данных. Поскольку крайний левый дробный бит всегда является 1, является ненужным сохранить этот бит, и это является поэтому неявным (или скрытым). Таким образом n битная часть хранит n +1-bit номер. Формат IEEE также поддерживает Денормализованные Числа, которые имеют часть формы 0. f.
В формате IEEE смещаются представления экспоненты. Это означает, что фиксированное значение, смещение, вычтено из поля экспоненты, чтобы получить истинное значение экспоненты. Например, если поле экспоненты составляет 8 битов, то числа 0 до 255 представлены, и существует смещение 127. Обратите внимание на то, что некоторые значения экспоненты резервируются для отмечающего Inf (бесконечность), NaN (не число) и денормализованные числа, таким образом, истинные значения экспоненты лежат в диапазоне от-126 до 127. См. Inf и NaN для получения дополнительной информации.
IEEE формат с плавающей точкой с двойной точностью является 64-битным словом, разделенным на 1-битный индикатор s знака, 11-битный смещенный порядок e и 52-битная часть f.

Отношением между форматом с двойной точностью и представлением вещественных чисел дают
Смотрите Исключительную Арифметику для получения дополнительной информации.
IEEE формат с плавающей точкой с одинарной точностью является 32-битным словом, разделенным на 1-битный индикатор s знака, 8-битный смещенный порядок e и 23-битный дробный f.
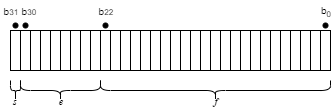
Отношением между форматом с одинарной точностью и представлением вещественных чисел дают
Смотрите Исключительную Арифметику для получения дополнительной информации.
Полуточность IEEE формат с плавающей точкой является 16-битным словом, разделенным на 1-битный индикатор s знака, 5-битный смещенный порядок e и 10-битный дробный f.
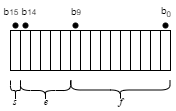
Числа полуточности поддерживаются в MATLAB® и Simulink®. Для получения дополнительной информации смотрите half и тип данных полуточности в Simulink.
Область значений номера дает пределы представления. Точность дает расстояние между последовательными числами в представлении. Область значений и точность числа с плавающей запятой IEEE зависят от определенного формата.
Область значений представимых чисел для числа с плавающей запятой IEEE с битами f, выделенными для части, биты e, выделенные для экспоненты и смещения e, данного bias = 2 (e −1) −1, приведена ниже.

где
Нормированные положительные числа заданы в области значений 2 (1−bias) к (2−2−f) 2bias.
Нормированные отрицательные числа заданы в области значений −2 (1−bias) к − (2−2−f) 2bias.
Положительные числа, больше, чем (2−2−f) 2bias и отрицательные числа меньше, чем − (2−2−f) 2bias, являются переполнением.
Положительные числа меньше чем 2 (1−bias) и отрицательные числа, больше, чем −2 (1−bias), являются или потерями значимости или денормализованными числами.
Нуль дан специальной комбинацией двоичных разрядов, где e = 0 и f = 0.
Переполнение и потери значимости следуют из исключительных арифметических условий. Числа с плавающей запятой вне заданной области значений всегда сопоставляются с ±Inf.
Примечание
Можно использовать команды MATLAB realmin и realmax определить динамический диапазон значений с плавающей точкой с двойной точностью для вашего компьютера.
Число с плавающей запятой является только приближением “истинного” значения из-за конечного размера слова. Поэтому важно иметь понимание точности (или точность) результата с плавающей точкой. Значение v с точностью q задано v ± q. Для чисел с плавающей запятой IEEE,
v = (−1) s (2e–bias) (1. f
и
q = 2–f × 2e–bias
Таким образом точность сопоставлена с количеством битов в дробном поле.
Область значений, смещение и точность для поддерживаемых типов данных с плавающей точкой даны в приведенной ниже таблице.
Тип данных | Низкий предел | Высокий предел | Смещение экспоненты | Точность |
|---|---|---|---|---|
| Половина | 2−14 ≈ 6.1·10−5 | (2−2-10) ·215≈ 6.5·104 | 15 | 2−10 ≈ 10−3 |
Единственный | 2−126 ≈ 10−38 | 2128 ≈ 3 · 1038 | 127 | 2−23 ≈ 10−7 |
'double' | 2−1022 ≈ 2 · 10−308 | 21024 ≈ 2 · 10308 | 1023 | 2−52 ≈ 10−16 |
Поскольку числа с плавающей запятой представлены с помощью знака/величины, существует два представления нуля, одного положительного и одного отрицательного. Для обоих представлений e = 0 и f.0 = 0.0.
Стандарт IEEE 754 задает методы и процедуры так, чтобы к предсказуемым результатам привели независимо от аппаратной платформы. Денормализованные числа, Inf, и NaN заданы, чтобы иметь дело с исключительной арифметикой (потеря значимости и переполнение).
Если потеря значимости или переполнение обработаны как Inf или NaN, затем значительный процессор наверху требуется, чтобы иметь дело за этим исключением. Несмотря на то, что Стандарт IEEE 754 задает методы и процедуры, чтобы иметь дело с исключительными арифметическими условиями сопоставимым способом, производители микропроцессора могут обработать эти условия способами, которые вылетают от стандарта.
Денормализованные числа используются, чтобы обработать случаи исчезновения порядка. Когда экспонента результата слишком мала (i.e., отрицательная экспонента со слишком большой величиной), результат денормализовывается сдвигом права часть и отъезд экспоненты в ее минимальном значении. Использование денормализованных чисел также упоминается как постепенная потеря значимости. Без денормализованных чисел, разрыва между самым маленьким представимым ненулевым номером и нулем намного более широко, чем разрыв между самым маленьким представимым ненулевым номером и следующим большим числом. Постепенные заливки потери значимости, которые разрывают и уменьшают удар исчезновения порядка к уровню, сопоставимому с округлением среди нормированных чисел. Денормализованные числа предоставляют расширенный спектр для небольших чисел за счет точности.
Арифметика, включающая Inf (бесконечность) обработана как ограничивающий случай арифметики действительных чисел с бесконечными значениями, заданными как те вне области значений представимых чисел или − ∞ ≤ (представимые числа) < ∞. За исключением особых случаев, обсужденных ниже (NaN), любая арифметическая операция, включающая Inf выражения InfInf представлен самым большим смещенным порядком, позволенным форматом и частью нуля.
NaN (не число) является символьной сущностью, закодированной в формате с плавающей точкой. Существует два типа NaN: сигнализация и подавляет шумы. Сигнальный NaN сигнализирует о недопустимом исключении операции. Тихий NaN распространяет почти через каждую арифметическую операцию, не сигнализируя об исключении. Следующие операции приводят к NaN: ∞ – ∞, – ∞ + ∞, 0× ∞, 0/0, и ∞ / ∞.
Оба сигнальных NaN и тихий NaN представлены самым большим смещенным порядком, позволенным форматом и ненулевой частью. Комбинация двоичных разрядов для тихого NaN дан 0. f, где старший значащий бит в f должен быть тем. Комбинация двоичных разрядов для сигнального NaN дан 0. f, где старший значащий бит в f должен быть нулем и по крайней мере одним из остающихся битов, должен быть ненулевым.