Для любого значения во вселенной беседы традиционная функция принадлежности типа 1 имеет одно значение членства. Поэтому, в то время как функция принадлежности типа 1 моделирует степень членства в данном лингвистическом наборе, это не моделирует неопределенность в степени членства. Чтобы смоделировать такую неопределенность, можно использовать функции принадлежности типа 2 интервала. В таких функциях принадлежности типа 2 степень членства может иметь область значений значений.
Для примеров, которые используют тип 2 нечеткие системы вывода, смотрите Нечеткое Управление ПИДом с Типом 2 FIS и Предскажите Хаотические Временные ряды Используя Тип 2 FIS.
Функция принадлежности типа 2 интервала задана верхней и более низкой функцией принадлежности. Верхняя функция принадлежности (UMF) эквивалентна традиционной функции принадлежности типа 1. Более низкая функция принадлежности (LMF) меньше чем или равна верхней функции принадлежности для всех возможных входных значений. Областью между UMF и LMF является footprint of uncertainty (FOU). Следующая схема показывает (красный) UMF, (синий) LMF, и FOU (заштрихованный) для типа 2 треугольная функция принадлежности.
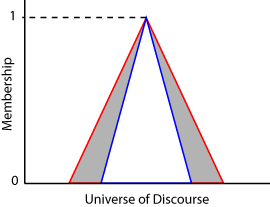
Для каждого входного значения во вселенной беседы степень членства является областью значений значений между LMF и значений UMF.
Используя программное обеспечение Fuzzy Logic Toolbox™, можно создать и тип 2 Mamdani и Sugeno нечеткие системы вывода.
В типе 2 системы Mamdani оба функции принадлежности ввода и вывода являются нечеткими множествами типа 2.
В типе 2 системы Sugeno только входные функции принадлежности являются нечеткими множествами типа 2. Выходные функции принадлежности совпадают с для типа 1 системой Sugeno — постоянный или линейная функция входных значений.
Чтобы создать тип 2 Mamdani и системы Sugeno, использовать mamfistype2 и sugfistype2 объекты, соответственно. Эти объекты имеют те же параметры как тип 1 mamfis и sugfis объекты наряду с дополнительным TypeReductionMethod параметр.
Можно также создать тип 2 нечеткая система вывода путем преобразования существующей системы типа 1, такой как одно созданное использование genfis функция. Для этого используйте convertToType2 функция.
Если вы создаете тип 2 нечеткая система вывода, вы можете:
Оцените нечеткую систему с помощью evalfis функции
Симулируйте нечеткую систему с помощью блока Fuzzy Logic Controller
Настройте параметры нечеткой системы с помощью tunefis функция
Развернитесь нечеткая система как описано в Развертывают Нечеткие Системы Вывода
Для типа 2 нечеткие системы вывода входные значения являются fuzzified путем нахождения соответствующей степени членства и в UMFs и в LMFs от антецедента правила. Выполнение так генерирует два нечетких значения для каждой функции принадлежности типа 2. Например, размывание в следующем рисунке показывает значение членства в верхней функции принадлежности (fU) и более низкая функция принадлежности (fL).
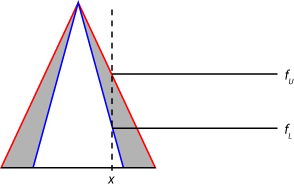
Затем область значений правила, запускающего сильные места, найдена путем применения нечеткого оператора к fuzzified значениям функций принадлежности типа 2 как показано в следующем рисунке. Максимальное значение этой области значений (wU) является результатом применения нечеткого оператора к нечетким значениям от UMFs. Минимальное значение (wL) является результатом применения нечеткого оператора к нечетким значениям от LMFs
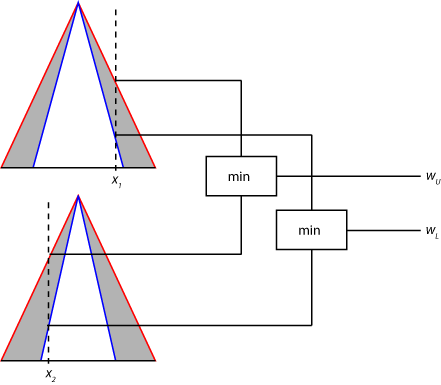
Предшествующая обработка является тем же самым и для систем Mamdani и для Sugeno.
Для системы Mamdani, клипы метода значения (min значение) или шкалы (prod значение) UMF и LMF выходной функции принадлежности типа 2 с помощью правила, запускающего пределы области значений. Этот процесс производит выходное нечеткое множество для каждого правила. Следующий рисунок показывает выходное нечеткое множество (темно-серая область) произведенный путем применения min значение к (красному) UMF и (синий) LMF.
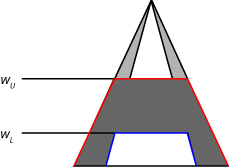
Для типа 2 система Sugeno уровень на выходе zi для i th правило вычисляется таким же образом что касается типа 1 система Sugeno.
Здесь, j является входным индексом, xj является значением j th входная переменная, и условия c являются верхними параметрами функции принадлежности
В отличие от типа 1 система Sugeno, правило, запускающее сильные места, не использовано, чтобы обработать следствие каждого правила. Вместо этого уровень на выходе и правило, запускающее сильные места, используются во время процесса агрегации.
Цель этапа агрегации состоит в том, чтобы вывести одно нечеткое множество типа 2 из правила выходные нечеткие множества.
Для типа 2 система Mamdani программное обеспечение находит составной тип 2 нечеткими множествами путем применения метода агрегации к UMFs и LMFs выходных нечетких множеств всех правил. Следующий рисунок показывает агрегацию двух нечетких множеств типа 2 (выходные параметры для системы 2D правила) использование max агрегация.
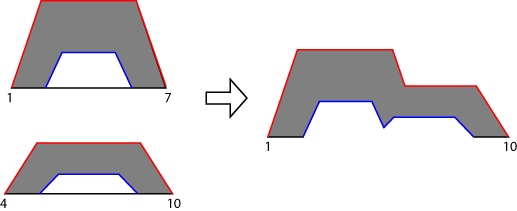
Для типа 2 система Sugeno совокупное нечеткое множество выведено с помощью следующих шагов:
Сортировка уровней на выходе правила (zi) от всех правил в порядок по возрастанию. Эти значения уровня на выходе задают вселенную беседы для составного типа 2 нечетких множества.
Для каждого уровня на выходе задайте значение UMF с помощью максимального значения диапазона увольнения от соответствующего правила.
Для каждого уровня на выходе задайте значение LMF с помощью минимального значения диапазона увольнения от соответствующего правила.
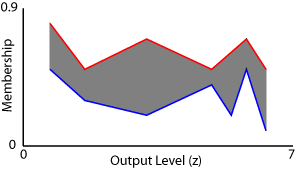
Например, предположите, что у вас есть тип 2 система Sugeno с семью правилами. Далее, примите, что эти правила имеют следующие уровни на выходе и запускающий пределы области значений.
| Правило | Уровень на выходе (z) | Минимальное значение увольнения | Максимальное значение увольнения |
|---|---|---|---|
| 1 | 6.3 | 0.1 | 0.5 |
| 2 | 4.9 | 0.4 | 0.5 |
| 3 | 1.6 | 0.3 | 0.5 |
| 4 | 5.8 | 0.5 | 0.7 |
| 5 | 5.4 | 0.2 | 0.6 |
| 6 | 0.7 | 0.5 | 0.8 |
| 7 | 3.2 | 0.2 | 0.7 |
Следующий рисунок показывает агрегированное нечеткое множество типа 2 для этой системы Sugeno с ее связанным (красным) UMF и (синий) LMF.
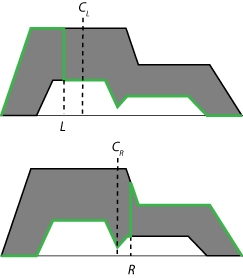
Чтобы найти итоговое четкое выходное значение для процесса вывода, составной тип, 2 нечетких множества сначала уменьшаются до нечеткого множества типа 1 интервала, которое является областью значений с нижним пределом cL и верхний предел cR. Это нечеткое множество типа 1 интервала обычно упоминается как центроид нечеткого множества типа 2. В теории этот центроид является средним значением центроидов всех нечетких множеств типа 1, встроенных в нечеткое множество типа 2. На практике не возможно вычислить точные значения cL и cR. Вместо этого итеративные методы сокращения типа используются, чтобы оценить эти значения.
Для данного составного типа 2 нечетких множества, приближенные значения cL и cR являются центроидами следующих (зеленых) нечетких множеств типа 1.
Математически, эти центроиды найдены с помощью следующих уравнений. [1]
Здесь:
N является количеством выборок, взятых через область значений выходной переменной, заданное использование evalfisOptions.
xi является i th выборка выходного значения.
μumf является верхней функцией принадлежности.
μlmf является более низкой функцией принадлежности.
L и R является switch points, которые оцениваются различными методами сокращения типа. Для списка поддерживаемых методов см. Методы Сокращения Типа.
И для систем Mamdani и для Sugeno, финал defuzzified выходное значение (y) является средним значением двух центроидных значений от процесса сокращения типа.
Программное обеспечение Fuzzy Logic Toolbox поддерживает четыре метода сокращения встроенного типа. Эти алгоритмы отличаются по своим методам инициализации, предположениям, вычислительному КПД и завершающим работу условиям.
Чтобы установить метод сокращения типа для типа 2 нечеткая система, установите TypeReduction свойство mamfistype2 или sugfistype2 объект.
| Метод | TypeReduction значение свойства | Описание |
|---|---|---|
| Карник-Мендель (KM) [2] | "karnikmendel" | Первый метод сокращения типа разрабатывается |
| Расширенный Карник-Мендель (EKM) [3] | "ekm" | Модификация алгоритма Карник-Менделя с улучшенной инициализацией, измененным условием завершения, и повысила вычислительную эффективность |
| Итеративный алгоритм с условием остановки (IASC) [4] | "iasc" | Итеративное улучшение методов грубой силы |
| Расширенный итеративный алгоритм с условием остановки (EIASC) [5] | "eiasc" | Улучшенная версия алгоритма IASC |
В общем случае вычислительный КПД этих методов улучшается, когда вы спускаете таблицу.
Можно также использовать собственный метод сокращения типа. Для получения дополнительной информации смотрите Сборку Нечеткие Системы Используя Пользовательские Функции.
[1] Мендель, Джерри М., Hani Hagras, Woei-бледный Tan, Уильям В. Мелек и Хао Ин. Введение в управление нечеткой логикой типа 2: теория и приложения. Хобокен, Нью-Джерси: IEEE Press, John Wiley & Sons, 2014.
[2] Karnik, Нилеш Н. и Джерри М. Мендель. ‘Центроид Нечеткого множества Типа 2’. Информатика 132, № 1-4 (февраль 2001): 195–220. https://doi.org/10.1016/S0020-0255 (01) 00069-X.
[3] Ву, D. и Дж.М. Мендель, "Улучшенные алгоритмы Карник-Менделя", Транзакции IEEE в Нечетких Системах, издании 17, стр 923-934. (2009)
[4] Duran, K., Х. Берналь и М. Мельгарехо, "Улучшенный итеративный алгоритм для вычисления обобщенного центроида нечеткого множества типа 2 интервала", Годовое собрание североамериканского Нечеткого Общества Обработки информации, стр 190-194. (2008)
[5] Ву, D. и М. Не, "Сравнение и практические реализации алгоритмов сокращения типа для нечетких множеств типа 2 и систем", Продолжения FUZZ-IEEE, стр 2131-2138 (2011)