Выберите местоположения в интерактивном режиме
Можно использовать функции Mapping Toolbox™ и графический интерфейсы пользователя, чтобы взаимодействовать с картами, обоими в mapview и в цифрах созданный с axesm. В этом разделе описываются две полезных функции ввода графических данных, inputm и gcpmap. inputm функция (аналогичный MATLAB®
ginput функция), позволяет вам получать положение долготы широты клика мыши. gcpmap функция (аналогичный функции MATLAB get(gca,'CurrentPoint')) возвращает текущее положение мыши, также в широте и долготе.
Исследовать inputm со следующими командами, которые отображают карту оси с ее сеткой и затем запрашивают три клика мыши, местоположения которых хранятся как географические координаты в переменной points. Затем plotm графики функций точки вы щелкнули как красные маркеры. Отображение, которое вы видите, зависит от точек, которые вы выбираете:
axesm sinusoid framem on; gridm on points=inputm(3)
points =
-41.7177 -145.0293
7.9211 -0.5332
38.5492 149.2237plotm(points,'r*')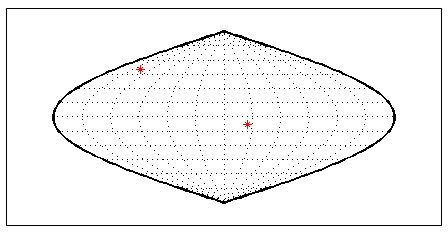
Примечание
Если вы щелкаете вне системы координат карты, inputm возвращает допустимую, но неправильную широту и долготу, даже при том, что точка, на которую вы указали, от карты.
Одна причина вы можете хотеть вручную идентифицировать точки на карте, состоит в том, чтобы в интерактивном режиме исследовать, сколько искажения проекция карты имеет в данных местоположениях. Например, можно питать данные полученными inputm к distortcalc функция, которая вычисляет область и угловые искажения в любом местоположении на отображенной карте оси. Если вы делаете настолько использующий points переменная, результаты предыдущих трех кликов мыши следующие:
[areascale,angledef] = distortcalc(points(1,1),points(1,2))
areascale =
1.0000
angledef =
85.9284[areascale,angledef] = distortcalc(points(2,1),points(2,2))
areascale =
1.0000
angledef =
3.1143[areascale,angledef] = distortcalc(points(3,1),points(3,2))
areascale =
1.0000
angledef =
76.0623Это указывает, что текущая (синусоидальная) проекция имеет свойство равной области, но показывает переменное угловое искажение через карту, менее близкую экватор и более близкий полюса.