Спроектируйте контроллер MPC для сервомеханизма положения

В этом примере показано, как спроектировать прогнозирующий контроллер модели для сервомеханизма положения с помощью MPC Designer.

Системная модель

Сервомеханизм положения состоит из двигателя постоянного тока, коробки передач, эластичного вала и загрузки.

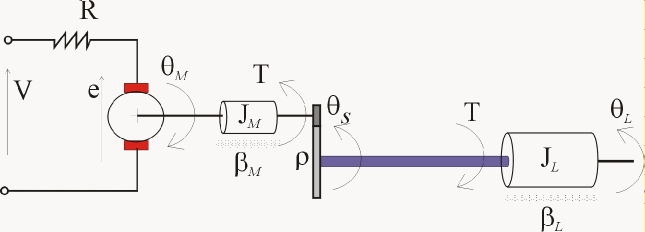
Дифференциальные уравнения, представляющие эту систему,

$\begin{array}{l} {\dot{ω}}_{L} = - \frac{k_{T}}{J_{L}} (θ_{L} - \frac{θ_{M}}{ρ}) - \frac{β_{L}}{J_{L}} ω_{L} \\ {\dot{ω}}_{M} = \frac{k_{M}}{J_{M}} (\frac{V - k_{M} ω_{M}}{R}) - \frac{β_{M} ω_{M}}{J_{M}} + \frac{k_{T}}{ρ J_{M}} (θ_{L} - \frac{θ_{M}}{ρ}) \end{array}$

где,

V является приложенным напряжением.
T является крутящим моментом, действующим на загрузку.
$ω_{L} = {\dot{θ}}_{L}$ скорость вращения загрузки.
$ω_{M} = {\dot{θ}}_{M}$ скорость вращения вала двигателя.

Остающиеся условия являются постоянными параметрами.

Постоянные параметры для модели сервомеханизма

Символ	Значение (единицы СИ)	Определение
_kT	1280.2	Жесткость при кручении
_kM	10	Моторная константа
_JM	0.5	Инерция двигателя
_JL	50_JM	Загрузите инерцию
ρ	20	Передаточное отношение
_βM	0.1	Моторный коэффициент вязкого трения
_βL	25	Загрузите коэффициент вязкого трения
R	20	Сопротивление якоря

Если вы задаете переменные состояния как

$x_{p} = {[\begin{matrix} θ_{L} & ω_{L} & θ_{M} & ω_{M} \end{matrix}]}^{T},$

затем можно смоделировать сервомеханизм как систему в пространстве состояний LTI.

$\begin{matrix} {\dot{x}}_{p} = [\begin{matrix} 0 & 1 & 0 & 0 \\ - \frac{k_{T}}{J_{L}} & - \frac{β_{L}}{J_{L}} & \frac{k_{T}}{ρ J_{L}} & 0 \\ 0 & 0 & 0 & 1 \\ \frac{k_{T}}{ρ J_{M}} & 0 & - \frac{k_{T}}{ρ^{2} J_{M}} & - \frac{β_{M} + \frac{k_{M}^{2}}{R}}{J_{M}} \end{matrix}] x_{p} + [\begin{matrix} 0 \\ 0 \\ 0 \\ \frac{k_{M}}{R J_{M}} \end{matrix}] V \\ θ_{L} = [\begin{matrix} 1 & 0 & 0 & 0 \end{matrix}] x_{p} \\ T = [\begin{matrix} k_{T} & 0 & - \frac{k_{T}}{ρ} & 0 \end{matrix}] x_{p} \end{matrix}$

Контроллер должен установить угловое положение загрузки, _θL, в требуемом значении путем корректировки приложенного напряжения, V.

Однако, поскольку эластичный вал имеет конечную прочность на срез, крутящий момент, T, должен остаться в области значений |T | ≤ 78,5 нм. Кроме того, источник напряжения физически ограничивает приложенное напряжение областью значений |V | ≤ 220 В.

Создайте модель объекта управления

Задайте константы модели.

Kt = 1280.2;  % Torsional rigidity
Km = 10;      % Motor constant
Jm = 0.5;     % Motor inertia
Jl = 50*Jm;   % Load inertia
N = 20;       % Gear ratio
Bm = 0.1;     % Rotor viscous friction
Bl = 25;      % Load viscous friction
R = 20;       % Armature resistance

Задайте матрицы пространства состояний, выведенные из уравнений модели.

A = [        0       1             0                0;
        -Kt/Jl  -Bl/Jl     Kt/(N*Jl)                0;
             0       0             0                1;
     Kt/(Jm*N)       0  -Kt/(Jm*N^2)  -(Bm+Km^2/R)/Jm];
B = [0; 0; 0; Km/(R*Jm)];
C = [  1  0       0  0;
      Kt  0   -Kt/N  0];
D = [0; 0];

Создайте модель в пространстве состояний.

plant = ss(A,B,C,D);

Откройте приложение MPC Designer

mpcDesigner

Импортируйте объект и задайте настройку сигнала

В MPC Designer, на вкладке MPC Designer, выбирают MPC Structure.

В диалоговом окне Define MPC Structure By Importing выберите plant модель объекта управления и присвоение ввод-вывод объекта образовывают канал к следующим типам сигнала:

Переменная, которой управляют — Напряжение, V
Измеренный выход — угловое положение Загрузки, _θL
Неизмеренный выход — Крутящий момент, T

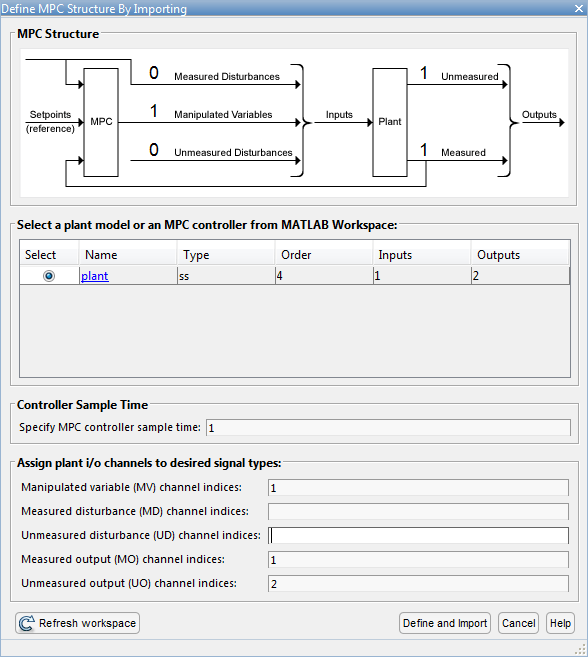
Нажмите Define and Import.

MPC Designer импортирует заданный объект к Data Browser. Следующее также добавляется к Data Browser:

mpc1 — Контроллер MPC по умолчанию создал использование plant как его внутренняя модель.
scenario1 — Сценарий симуляции по умолчанию. Результаты этой симуляции отображены в графиках Output Response и Input Response.

Задайте атрибуты канала ввода и вывода

На вкладке MPC Designer, в разделе Structure, нажимают I/O Attributes.

В диалоговом окне Input and Output Channel Specifications, для каждого канала ввода и вывода:

Задайте значимый Name и Unit.
Сохраните Nominal Value в его значении по умолчанию 0.

Задайте Scale Factor для нормализации сигнала. Выберите значение, которое аппроксимирует предсказанный рабочий диапазон сигнала:

Название канала	Минимальное значение	Максимальное значение	ScaleFactor
`Voltage`	– 220 В	220 В	440
`Theta`	– Радианы π	π радианы	6.28
`Torque`	– 78.5 Nm	78.5 Nm	157

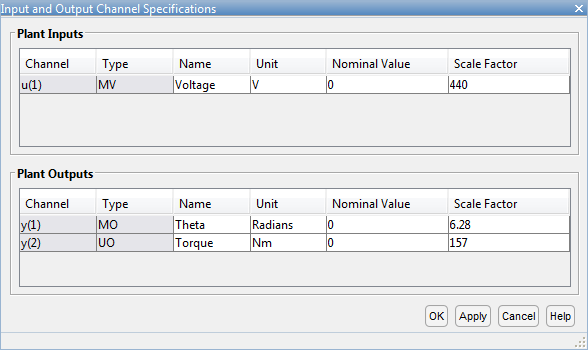
Нажмите OK, чтобы обновить атрибуты канала и закрыть диалоговое окно.

Измените сценарий, чтобы симулировать переходной процесс углового положения

В разделе Scenario, Edit Scenario выпадающий список, выбирают scenario1 изменить сценарий симуляции по умолчанию.

В диалоговом окне Simulation Scenario задайте Simulation duration 10 секунды.

В таблице Reference Signals сохраните настройку по умолчанию для первого канала. Эти настройки создают Step изменение 1 радиан в заданном значении углового положения в Time 1 второй.

Для второго выхода, в Signal выпадающий список, выбирают Constant сохранить заданное значение крутящего момента по его номинальной стоимости.

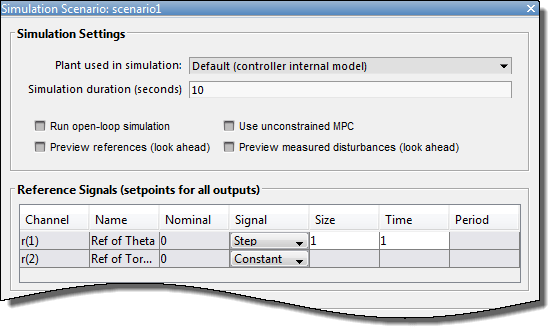
Нажмите OK.

Выполнение приложения симуляция с новыми настройками сценария и обновлениями Input Response и графики Output Response.

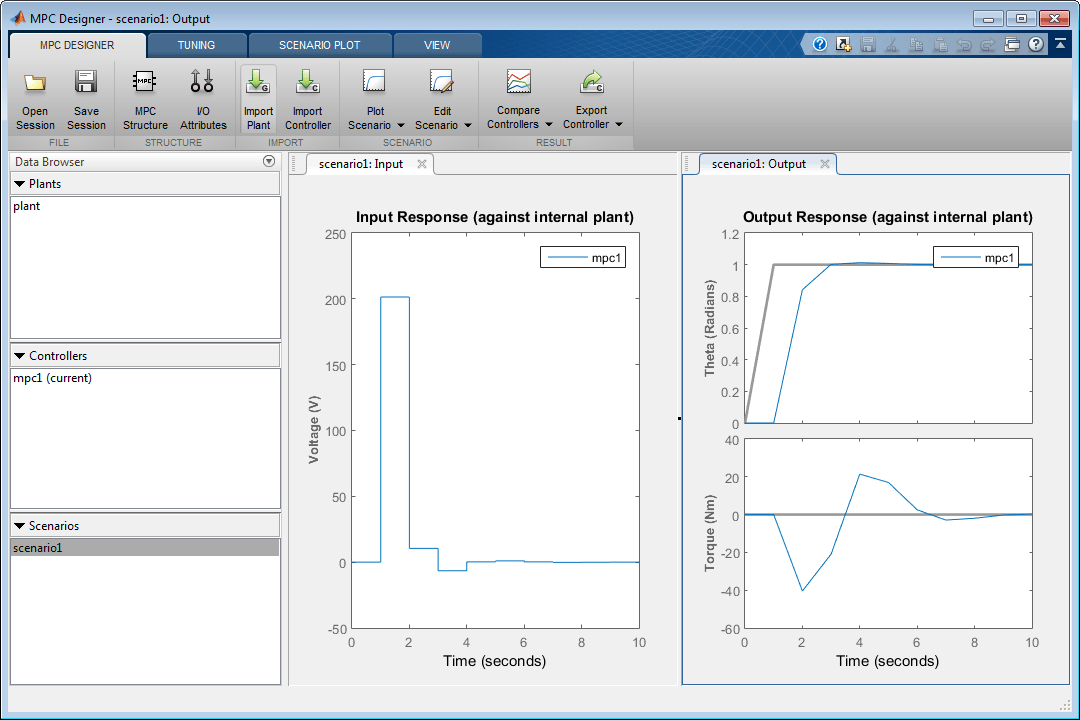
Задайте шаг расчета контроллера и горизонты

На вкладке Tuning, в разделе Horizon, задают Sample time 0.1 секунды.

Для заданного шага расчета _Ts, и желаемое время отклика _Tr = 2 секунды, выбирает горизонт предсказания, p, такой что:

$T_{r} \approx p T_{s} .$

Поэтому задайте Prediction horizon 20.

Задайте Control horizon 5.

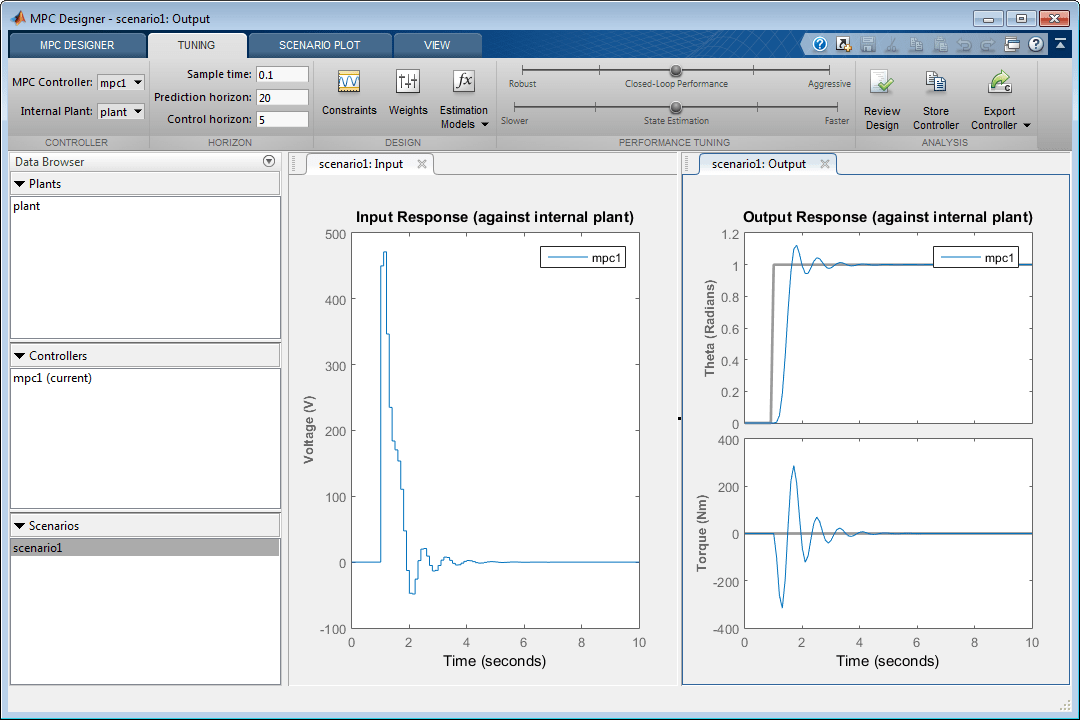
Когда вы обновляете шаг расчета и значения горизонта, Input Response и графики Output Response обновляются автоматически. Оба входное напряжение и значения крутящего момента превышают ограничения, заданные в технических требованиях системной модели.

Задайте ограничения

В разделе Design выберите Constraints.

В диалоговом окне Constraints, в разделе Input Constraints, задают Min и значения напряжения Max для переменной, которой управляют, (MV).

В разделе Output Constraints задайте Min и значения крутящего момента Max для неизмеренного выхода (UO).

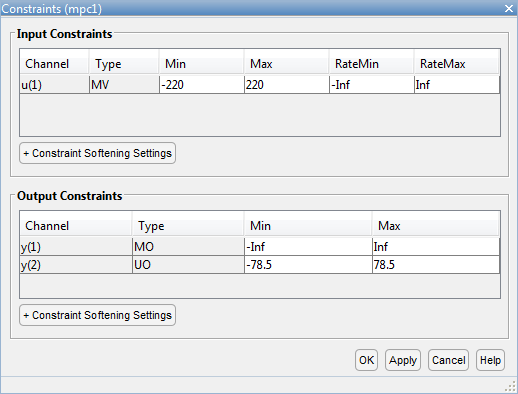
Нет никаких дополнительных ограничений, который является другими ограничениями, остаются в их максимальных и минимальных значениях по умолчанию, —Inf и Inf соответственно

Нажмите OK.

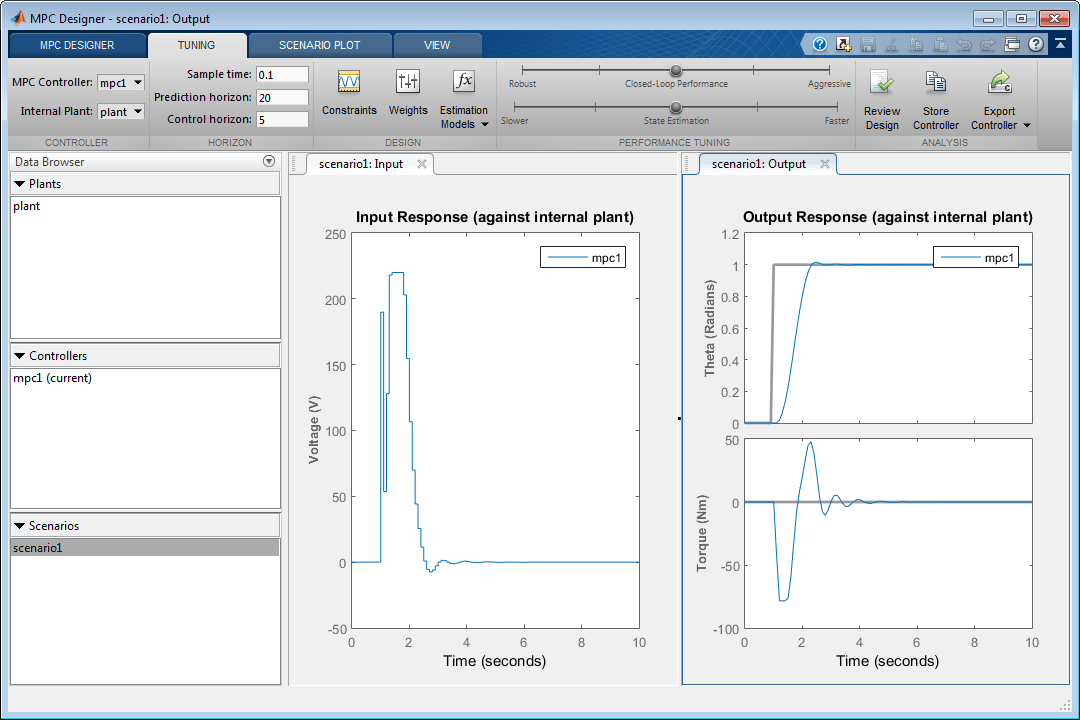
Графики отклика обновляются, чтобы отразить новые ограничения. В графике Input Response во входном напряжении существуют нежелательные большие изменения.

Задайте настраивающиеся веса

В разделе Design выберите Weights.

В диалоговом окне Weights, в таблице Input Weights, увеличивают переменную Rate Weight, которой управляют.

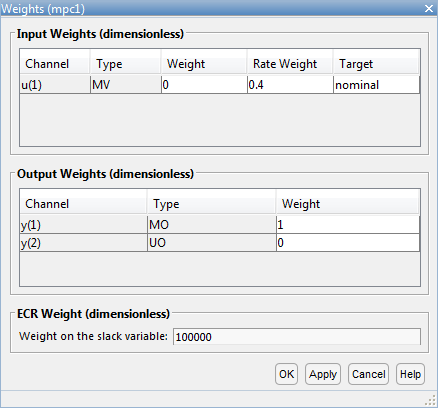
Настраивающимся Weight для переменной, которой управляют, (MV) является 0. Этот вес указывает, что контроллер может позволить входному напряжению варьироваться в его ограниченной области значений. Увеличенный Rate Weight ограничивает размер переменных изменений, которыми управляют.

Поскольку цель управления для углового положения загрузки, чтобы отследить ее заданное значение, настраивающимся Weight на измеренном выходе является 1. Нет никакого заданного значения для прикладного крутящего момента, таким образом, контроллер может позволить второму выходу варьироваться в рамках его ограничений. Поэтому Weight на неизмеренном выходе (UO) является 0, который позволяет контроллеру проигнорировать заданное значение крутящего момента.

Нажмите OK.

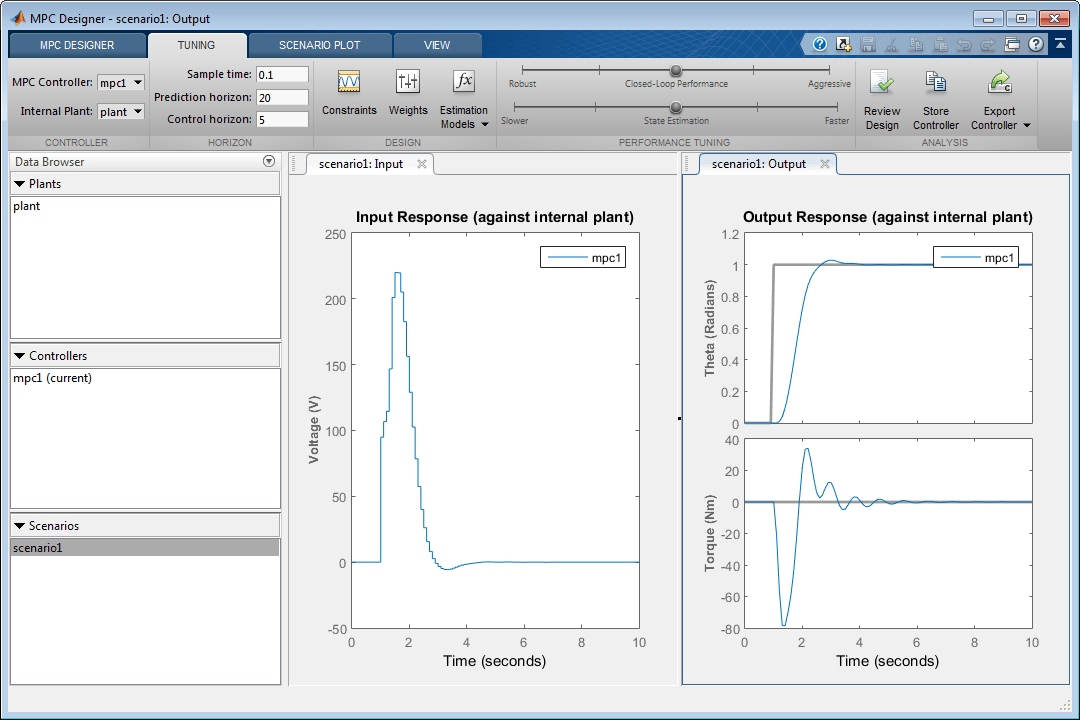
Графики отклика обновляются, чтобы отразить увеличенный вес уровня. Input Response более сглажен с меньшими изменениями напряжения.

Исследуйте Выходной ответ

В графике Output Response щелкните правой кнопкой по области построения Theta и выберите Characteristics> Peak Response.

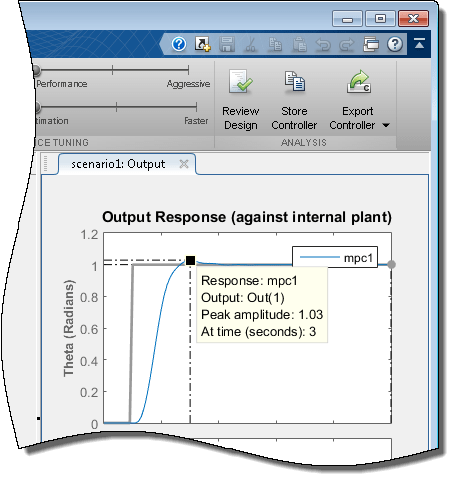
Пиковый выходной ответ происходит во время 3 секунд перерегулирование имеющее 3%. Поскольку ступенчатое изменение опорного сигнала в 1 секунду, у контроллера есть пиковое время 2 секунд.

Улучшите время отклика контроллера

Перетащите ползунок Closed-Loop Performance к праву произвести больше ответа Aggressive. Чем далее вы перетаскиваете ползунок направо, тем быстрее контроллер отвечает. Выберите положение ползунка, таким образом, что максимальная чувствительность происходит в 2,7 секунды.

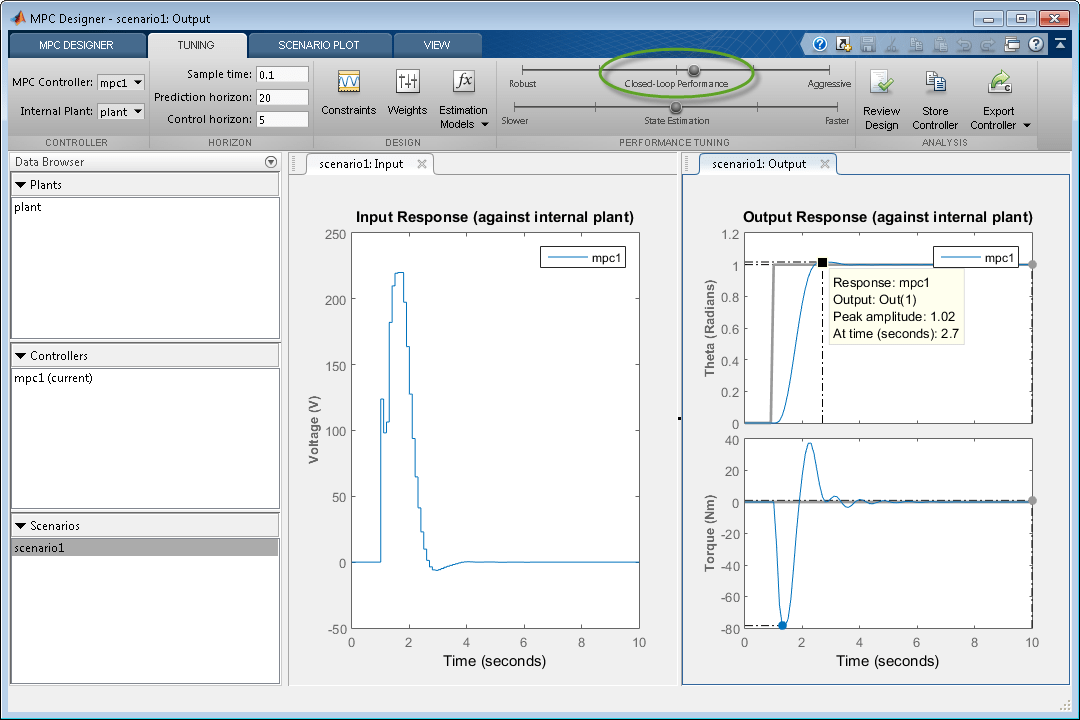
Итоговое пиковое время контроллера составляет 1,7 секунды. Сокращение времени отклика дальнейшие результаты в чрезмерно агрессивных изменениях входного напряжения.

Сгенерируйте и запущенный СКРИПТ MATLAB

В разделе Analysis кликните по стреле Export Controller.

Под Export Controller нажмите Generate Script.

В диалоговом окне Script Generate MATLAB^® установите флажок рядом с scenario1.

Нажмите Generate Script.

Приложение экспортирует копию модели объекта управления, plant_C, к рабочему пространству MATLAB, наряду с входом симуляции и опорными сигналами.

Кроме того, приложение генерирует следующий код в редакторе MATLAB.

%% create MPC controller object with sample time
mpc1 = mpc(plant_C, 0.1);
%% specify prediction horizon
mpc1.PredictionHorizon = 20;
%% specify control horizon
mpc1.ControlHorizon = 5;
%% specify nominal values for inputs and outputs
mpc1.Model.Nominal.U = 0;
mpc1.Model.Nominal.Y = [0;0];
%% specify scale factors for inputs and outputs
mpc1.MV(1).ScaleFactor = 440;
mpc1.OV(1).ScaleFactor = 6.28;
mpc1.OV(2).ScaleFactor = 157;
%% specify constraints for MV and MV Rate
mpc1.MV(1).Min = -220;
mpc1.MV(1).Max = 220;
%% specify constraints for OV
mpc1.OV(2).Min = -78.5;
mpc1.OV(2).Max = 78.5;
%% specify overall adjustment factor applied to weights
beta = 1.2712;
%% specify weights
mpc1.Weights.MV = 0*beta;
mpc1.Weights.MVRate = 0.4/beta;
mpc1.Weights.OV = [1 0]*beta;
mpc1.Weights.ECR = 100000;
%% specify simulation options
options = mpcsimopt();
options.RefLookAhead = 'off';
options.MDLookAhead = 'off';
options.Constraints = 'on';
options.OpenLoop = 'off';
%% run simulation
sim(mpc1, 101, mpc1_RefSignal, mpc1_MDSignal, options);

В Окне MATLAB, во вкладке Editor, выбирают Save.

Завершите диалоговое окно Save и затем нажмите Save.

Во вкладке Editor нажмите Run.

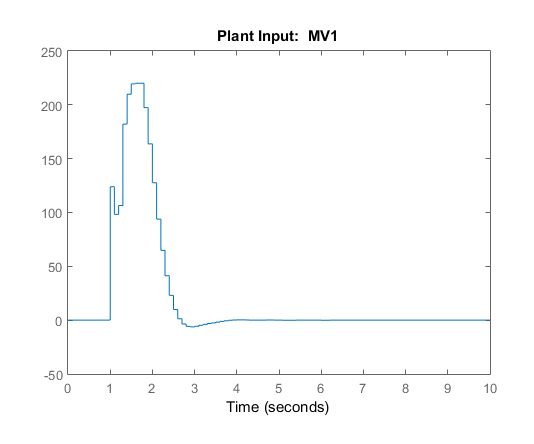
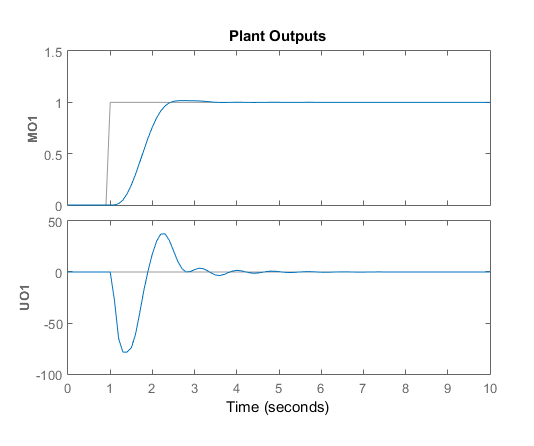
Скрипт создает контроллер, mpc1, и запускает сценарий симуляции. Ответы ввода и вывода совпадают с результатами симуляции из приложения.

Подтвердите эффективность контроллера в Simulink

Если у вас есть модель Simulink^® вашей системы, можно симулировать контроллер и подтвердить ее эффективность. Функциональность Simulink не поддерживается в MATLAB Online™.

Откройте модель.

open_system('mpc_motor')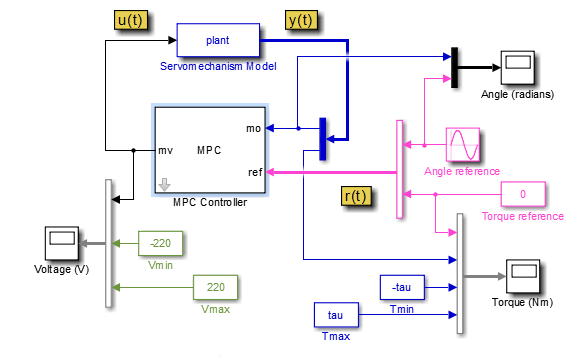

Эта модель использует блок MPC Controller, чтобы управлять объектом сервомеханизма. Блок Servomechanism Model уже сконфигурирован, чтобы использовать plant модель от рабочего пространства MATLAB.

Исходный блок Angle reference создает синусоидальный опорный сигнал с частотой 0.4 рад/секунда и амплитуда π.

Дважды кликните блок MPC Controller.

В диалоговом окне MPC Controller Block Parameters задайте MPC Controller от рабочего пространства MATLAB. Используйте mpc1 контроллер создал использование сгенерированного скрипта.

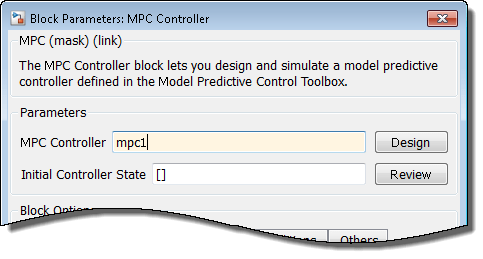
Нажмите OK.

В командной строке MATLAB задайте ограничительную переменную величины крутящего момента.

tau = 78.5;

Модель использует это значение, чтобы построить ограничительные пределы на крутящем моменте выход scope.

В окне модели Simulink нажмите Run, чтобы симулировать модель.

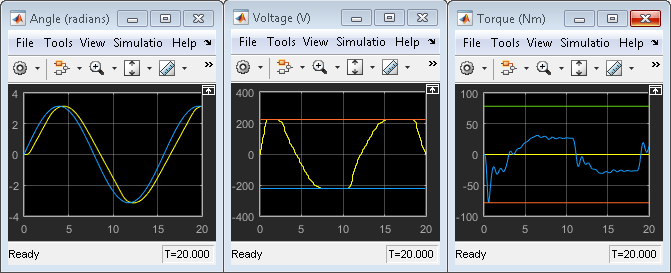
В осциллографе Angle выходной ответ, желтый, отслеживает заданное значение углового положения, синее, тесно.

Смотрите также

mpc | MPC Controller | MPC Designer

Документация