Многоцелевые алгоритмы оптимизации

Многоцелевое определение оптимизации

Существует два Optimization Toolbox™ многоцелевые решатели: fgoalattain и fminimax.

fgoalattain решает проблему сокращения набора нелинейных функций _Fi (x) ниже набора целей _F*i. С тех пор существует несколько функций _Fi (x), не всегда ясно, что это означает решать эту задачу, особенно когда вы не можете достигнуть всех целей одновременно. Поэтому проблема переформулирована к той, которая всегда четко определена.
unscaled goal attainment problem должен минимизировать максимум _Fi (x) – _F*i.
Существует полезное обобщение немасштабированной проблемы. Учитывая набор положительных весов _wi, goal attainment problem пытается найти, что x минимизирует максимум
$\frac{F_{i} (x) - F_{i}^{*}}{w_{i}} .$ (1)
Эта минимизация, как предполагается, выполняется при удовлетворении всем типам ограничений: c (x) ≤ 0, ceq (x) = 0, A·x ≤ b, Aeq·x = beq и l ≤ x ≤ u.
Если вы устанавливаете все веса, равные 1 (или любая другая положительная константа), целевая проблема достижения совпадает с немасштабированной целевой проблемой достижения. Если _F*i положителен, и вы устанавливаете все веса как _wi = _F*i, целевая проблема достижения становится минимизацией относительной разницы между функциями _Fi (x) и цели _F*i.
Другими словами, целевая проблема достижения состоит в том, чтобы минимизировать слабую переменную γ, заданную как максимум по i выражений в уравнении 1. Это подразумевает выражение, которое является формальным оператором целевой проблемы достижения:
$\min_{x, γ} γ$
таким образом, что F (x) – w · γ ≤ F*, c (x) ≤ 0, ceq (x) = 0, A·x ≤ b, Aeq·x = beq и l ≤ x ≤ u.
fminimax решает проблему минимизации максимума набора нелинейных функций согласно всем типам ограничений:
$\min_{x} \max_{i} F_{i} (x)$
таким образом, что c (x) ≤ 0, ceq (x) = 0, A·x ≤ b, Aeq·x = beq и l ≤ x ≤ u.
Безусловно, этой проблемой является особый случай немасштабированной целевой проблемы достижения с _F*i = 0 и _wi = 1.

Алгоритмы

Целевой метод достижения

В этом разделе описываются целевой метод достижения Gembicki [3]. Этот метод использует набор целей проекта, $F^{*} = {F_{1}^{*}, F_{2}^{*}, ..., F_{m}^{*}}$ , сопоставленный с набором целей, F (x) = {F ₁ (x), F ₂ (x)..., _Fm (x)}. Формулировка задачи позволяет целям быть под - или сверхдостигнута, позволяя разработчику быть относительно неточной о начальных целях проекта. Относительной степенью под - или сверхдостижение целей управляет вектор из взвешивания коэффициентов, w = {w ₁, w ₂..., _wm}, и описывают как стандартная задача оптимизации с помощью формулировки

\underset{γ \in ℜ, x \in Ω}{minimize} γ

(2)

таким образом, что $F_{i} (x) - w_{i} γ \leq F_{i}^{*}, i = 1, ..., m .$

Термин _wiγ вводит элемент застоя в проблему, которая в противном случае налагает, что целям твердо удовлетворяют. Вектор взвешивания, w, позволяет разработчику описать меру относительных компромиссов между целями. Например, установка взвешивающего векторного w, равного начальным целям, указывает, что тот же процент под - или сверхдостижение целей, F*, достигается. Можно включить трудные ограничения в проект путем обнуления особого фактора взвешивания (т.е. _wi = 0). Целевой метод достижения обеспечивает удобную интуитивную интерпретацию проблемы проектирования, которая является разрешимыми использующими стандартными процедурами оптимизации. Иллюстративные примеры использования целевого метода достижения в проекте системы управления могут быть найдены во фламандце ([10] и [11]).

Целевой метод достижения представлен геометрически на рисунке ниже в двух измерениях.

Рисунок 7-1, геометрическое представление целевого метода достижения

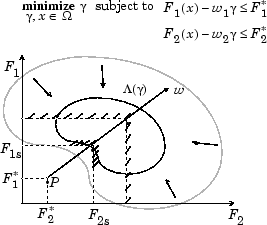
Спецификация целей, ${F_{1}^{*}, F_{2}^{*}}$ , задает целевую точку, P. Вектор взвешивания задает направление поиска от P до выполнимого функционального пространства, Λ (γ). Во время оптимизации варьируется γ, который изменяет размер выполнимой области. Границы ограничений сходятся к точке уникального решения F _1s, F _2s.

Улучшения алгоритма для целевого метода достижения

Целевой метод достижения имеет преимущество, что это может быть изложено как проблема нелинейного программирования. Характеристики проблемы могут также быть использованы в алгоритме нелинейного программирования. В последовательном квадратичном программировании (SQP) выбор оценочной функции для поиска линии не легок, потому что во многих случаях это затрудняет, чтобы “задать” относительную важность между улучшением целевой функции и сокращением нарушений ограничений. Это привело ко многим различным схемам построения оценочной функции (см., например, Щиттковского [36]). В целевом достижении, программирующем может быть более соответствующая оценочная функция, которой можно достигнуть путем изложения уравнения 2 как минимаксную проблему

\underset{x \in ℜ^{n}}{minimize} \max_{i} {Λ_{i}},

(3)

где

$Λ_{i} = \frac{F_{i} (x) - F_{i}^{*}}{w_{i}}, i = 1, ..., m .$

После аргумента Brayton и др. [1] для минимаксной оптимизации с помощью SQP, с помощью оценочной функции уравнения 30 для целевой проблемы достижения уравнения 3 дает

ψ (x, γ) = γ + \sum_{i = 1}^{m} r_{i} \cdot \max {0, F_{i} (x) - w_{i} γ - F_{i}^{*}} .

(4)

Когда оценочная функция уравнения 4 используется в качестве базиса процедуры поиска линии, затем, несмотря на то, что ψ (x, γ) может уменьшиться для шага в данном поисковом направлении, функциональном max Λ_i может как это ни парадоксально увеличиться. Это принимает ухудшение в худшей цели случая. Поскольку худшая цель случая ответственна за значение целевой функции γ, это принимает шаг, который в конечном счете увеличивает целевую функцию, которая будет минимизирована. С другой стороны ψ (x, γ) может увеличиться когда max Уменьшения Λ_i, подразумевая отклонение шага, который улучшает худшую цель случая.

После линий Brayton и др. [1], решение состоит в том, чтобы поэтому установить ψ (x), равный худшей цели случая, i.e.,

ψ (x) = \max_{i} Λ_{i} .

(5)

Проблема в целевом методе достижения состоит в том, что распространено использовать коэффициент взвешивания, равный 0, чтобы включить трудные ограничения. Оценочная функция уравнения 5 затем становится бесконечной для произвольных нарушений ограничений.

Чтобы преодолеть эту проблему, все еще сохраняя функции уравнения 5, оценочная функция объединена тем из уравнения 31, дав следующее:

ψ (x) = \sum_{i = 1}^{m} {\begin{array}{l} r_{i} \cdot \max {0, F_{i} (x) - w_{i} γ - F_{i}^{*}} & если w_{i} = 0 \\ \max_{i} Λ_{i}, i = 1, ..., m & в противном случае . \end{array}

(6)

Другой функцией, которая может быть использована в SQP, является целевая функция γ. От уравнений KKT можно показать, что приближение к Гессиану функции Лагранжа, H, должно иметь нули в строках и столбцах, сопоставленных с переменной γ. Однако это свойство не появляется, если H инициализируется как единичная матрица. H поэтому инициализирован и обеспечен, чтобы иметь нули в строках и столбцах, сопоставленных с γ.

Эти изменения делают Гессиан, H, неопределенный. Поэтому H будет иметь нули в строках и столбцах, сопоставленных с γ, за исключением диагонального элемента, который установлен в маленькое положительное число (например, 1e- 10). Это позволяет использование быстрого сходящегося положительного определенного метода QP, описанного в Решении для Квадратичного программирования.

Предыдущие модификации были реализованы в fgoalattain и, как находили, сделали метод более устойчивым. Однако из-за быстрой сходимости метода SQP, требование, чтобы оценочная функция строго уменьшалась иногда, требует большего количества вычислений функции, чем реализация SQP использование оценочной функции уравнения 30.

Минимизация максимальной цели

fminimax использует целевой метод достижения. Это берет цели 0 и веса 1. С этой формулировкой целевая проблема достижения становится

$\min_{i} \max_{x} (\frac{f_{i} (x) - g o a l_{i}}{w e i g h t_{i}}) = \min_{i} \max_{x} f_{i} (x),$

который является минимаксной проблемой.

Между прочим, вы можете ожидать fminimax превратить многоцелевую функцию в одну цель. Функция

f (x) = макс. (F ₁ (x)... F _j (x))

одна целевая функция должна минимизировать. Однако это не дифференцируемо, и цели Optimization Toolbox требуются, чтобы явиться гладкими. Поэтому минимаксная проблема формулируется как сглаженная целевая проблема достижения.

Ссылки

[1] Brayton, R. K. S. W. Директор, Г. Д. Хэчтель, и Л.Видигэл, “Новый Алгоритм для Статистического Проектирования схем На основе Приближенных методов ньютона и Функционального Разделения”, Транзакции IEEE на Схемах и Системах, издании CAS-26, стр 784-794, сентябрь 1979.

[2] Фламандец, П.Дж. и А.П. Пашкевич, Компьютер помог Проекту Системы управления Используя Многоцелевой Подход Оптимизации, Управление 1 985 Конференций, Кембридж, Великобритания, стр 174-179.

[3] Gembicki, F.W., “Векторная оптимизация для управления с индексами эффективности и чувствительности параметров”, Ph.D. Диссертация, случай западный резервный унив, Кливленд, OH, 1974.

[4] Изящество, A.C.W., “автоматизированный проект системы управления Используя методы оптимизации”, Ph.D. Тезис, Уэльский университет, Бангор, Гвинед, Великобритания, 1989.

[5] Ханьцы, S.P., “Глобально Конвергентный Метод Для Нелинейного программирования”, Журнал Теории Оптимизации и Приложений, Издания 22, p. 297, 1977.

[6] Мэдсен, K. и Х. Шджэер-Джэйкобсен, “Алгоритмы для худшей оптимизации допуска случая”, сделка IEEE схем и систем, издания CAS-26, сентябрь 1979.

[7] Пауэлл, M.J.D., “Алгоритм FAST для Нелинейных Ограниченных Вычислений Оптимизации”, Числовой Анализ, редактор Г.А. Уотсон, Примечания Лекции в Математике, Издании 630, Springer Verlag, 1978.

Документация