Чтобы задать параметры для решения УЧП, выберите Parameters из меню Solve. Набор решает параметры, отличается в зависимости от типа УЧП. После того, как вы настраиваете параметры, решаете УЧП путем выбора Solve PDE из меню Solve или путем нажатия![]() кнопки.
кнопки.
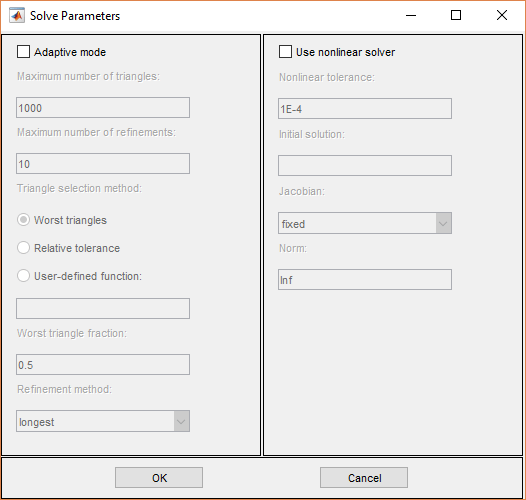
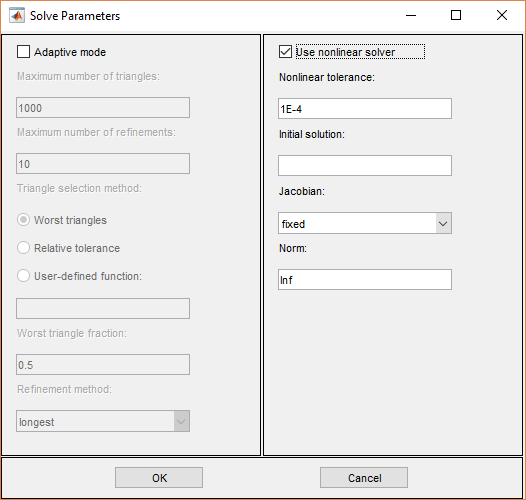
По умолчанию, нет конкретный решают параметры, используются, и эллиптические УЧП решены с помощью основного эллиптического решателя assempde. Опционально, адаптивный генератор mesh и решатель adaptmesh может использоваться. Для адаптивного режима следующие параметры доступны:
Adaptive mode. Переключите адаптивный режим вкл\выкл.
Maximum number of triangles. Максимальное количество новых треугольников позволило (может быть установлен в Inf). Значение по умолчанию вычисляется на основе текущей mesh.
Maximum number of refinements. Максимальное количество последовательных улучшений предпринято.
Triangle selection method. Существует два треугольных метода выбора, описанные ниже. Можно также предоставить собственную функцию.
Worst triangles. Этот метод выбирает все треугольники, которые хуже, чем часть значения худшего треугольника (значение по умолчанию: 0.5).
Relative tolerance. Этот метод выбирает треугольники с помощью критерия относительной погрешности (значение по умолчанию: 1E-3).
User-defined function. Введите имя пользовательского треугольного метода выбора. Смотрите уравнение Пуассона с Точечным источником и Адаптивное Улучшение Mesh для примера пользовательского треугольного метода выбора.
Function parameter. Параметр функции позволяет подстраивать треугольных методов выбора. Для худшего треугольного метода (pdeadworst), это - часть худшего значения, которое используется, чтобы определить который треугольники совершенствовать. Для метода относительной погрешности это - параметр допуска, который управляет, как хорошо решение соответствует УЧП.
Refinement method. Может быть regular или longest. Смотрите задают параметры Mesh в приложении PDE Modeler.
Если проблема нелинейна, т.е. параметры в УЧП непосредственно зависят от решения u, должен использоваться нелинейный решатель. Следующие параметры используются:
Use nonlinear solver. Переключите нелинейный решатель вкл\выкл.
Nonlinear tolerance. Параметр допуска для нелинейного решателя.
Initial solution. Исходное предположение. Может быть константа или функция x и y, данного как выражение MATLAB®, которое может быть выполнено на узлах текущей mesh.
Примеры: 1, и exp(x.*y). Дополнительный параметр, значения по умолчанию, чтобы обнулить.
Jacobian. Якобиевский метод приближения: fixed (значение по умолчанию), итерация фиксированной точки, lumped, “смешанное” (диагональное) приближение или full, полный якобиан.
Норма. Тип нормы, используемой в вычислениях невязка. Войдите как energy для энергетической нормы, или как действительный скалярный p, чтобы дать l p норма. Значением по умолчанию является Inf, бесконечность (максимум) норма.
Примечание
Адаптивный режим и нелинейный решатель могут использоваться вместе.
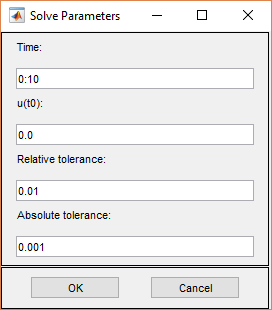
Решить параметры для параболических УЧП:
Время. Вектор MATLAB времен, в которые должно быть сгенерировано решение параболического УЧП. Соответствующий отрезок времени зависит от динамики проблемы.
Примеры: 0:10, и logspace(-2,0,20)
u(t0). Начальное значение u (t 0) для параболической проблемы УЧП начальное значение может быть константой или вектор-столбцом значений на узлах текущей mesh.
Relative tolerance. Параметр относительной погрешности для решателя ОДУ, который используется для решения зависящей от времени части параболической проблемы УЧП.
Absolute tolerance. Параметр абсолютной погрешности для решателя ОДУ, который используется для решения зависящей от времени части параболической проблемы УЧП.
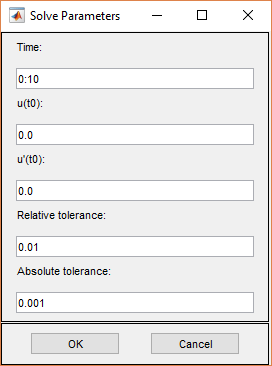
Решить параметры для гиперболических УЧП:
Время. Вектор MATLAB времен, в которые должно быть сгенерировано решение гиперболического УЧП. Соответствующий отрезок времени зависит от динамики проблемы.
Примеры: 0:10, и logspace(-2,0,20).
u(t0). Начальное значение u (t 0) для гиперболической проблемы УЧП. Начальное значение может быть константой или вектор-столбцом значений на узлах текущей mesh.
u'(t0). Начальное значение (t 0) для гиперболической проблемы УЧП. Можно использовать те же форматы что касается u(t0).
Relative tolerance. Параметр относительной погрешности для решателя ОДУ, который используется для решения зависящей от времени части гиперболической проблемы УЧП.
Absolute tolerance. Параметр абсолютной погрешности для решателя ОДУ, который используется для решения зависящей от времени части гиперболической проблемы УЧП.
Для УЧП собственного значения единственные решают параметр, Eigenvalue search range, двухэлементный вектор, задавая интервал на вещественной оси как поисковая область значений для собственных значений. Левой стороной может быть -Inf.
Примеры: [0 100], [-Inf 50]
Прежде, чем решить нелинейный эллиптический УЧП в приложении PDE Modeler, выберите Solve Parameters. Затем выберите Use nonlinear solver и нажмите OK.