В этом примере показано, как решить уравнение волны для поперечных колебаний мембраны на квадрате. Мембрана фиксируется в левых и правых сторонах и свободна в верхних и более низких сторонах. Этот пример использует приложение PDE Modeler. Для программируемого рабочего процесса смотрите уравнение Волны на Квадратной Области.
Уравнение волны является гиперболическим УЧП:
Чтобы решить эту задачу в приложении PDE Modeler, выполните эти шаги:
Откройте приложение PDE Modeler при помощи pdeModeler команда.
Отобразите линии сетки путем выбора Options> Grid.
Выровняйте новые формы к линиям сетки путем выбора Options> Snap.
Чертите квадрат с углами в (-1,-1), (-1,1), (1,1), и (1,-1). Для этого сначала нажмите![]() кнопку. Затем кликните по одному из углов с помощью правой кнопки мыши и перетащите, чтобы чертить квадрат. Правая кнопка мыши ограничивает форму, которую вы чертите, чтобы быть квадратом, а не прямоугольником.
кнопку. Затем кликните по одному из углов с помощью правой кнопки мыши и перетащите, чтобы чертить квадрат. Правая кнопка мыши ограничивает форму, которую вы чертите, чтобы быть квадратом, а не прямоугольником.
Также можно использовать pderect функция:
pderect([-1 1 -1 1])
Проверяйте, что режим приложения установлен в Generic Scalar.
Задайте граничные условия. Для этого переключитесь на граничный режим путем нажатия![]() кнопки или выбора Boundary> Boundary Mode. Выберите левые и правые контуры. Затем выберите Boundary> Specify Boundary Conditions и задайте граничное условие Дирихле u = 0. Это граничное условие является по умолчанию (
кнопки или выбора Boundary> Boundary Mode. Выберите левые и правые контуры. Затем выберите Boundary> Specify Boundary Conditions и задайте граничное условие Дирихле u = 0. Это граничное условие является по умолчанию (h = 1, r = 0), таким образом, вы не должны изменять его.
Для нижней части и главных контуров, установленных Нейманово граничное условие ∂u / ∂ n = 0. Для этого установите g = 0, q = 0.
Задайте коэффициенты путем выбора PDE PDE Specification или нажатия кнопки PDE на панели инструментов. Выберите тип Hyperbolic УЧП и задайте c = 1, a = 0, f = 0, и d = 1.
Инициализируйте mesh путем выбора Mesh> Initialize Mesh. Совершенствуйте mesh путем выбора Mesh> Refine Mesh.
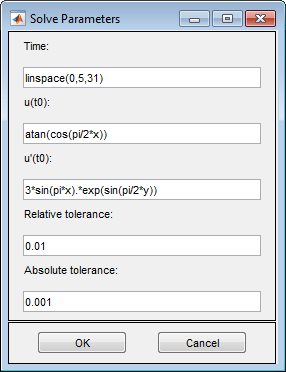
Установите времена решения. Для этого выберите Solve> Parameters. Создайте линейно распределенный временной вектор от 0 до 5 секунд путем установки времени решения на linspace(0,5,31).
В том же диалоговом окне задайте начальные условия для уравнения волны. Для решения хорошего поведения начальные значения должны совпадать с граничными условиями. Если начальным временем является t = 0, то следующие начальные значения, которые удовлетворяют граничным условиям: atan(cos(pi/2*x)) для u(0) и 3*sin(pi*x).*exp(sin(pi/2*y)) для ∂u / ∂ t,
Обратная функция тангенса и показательная функция вводят больше режимов в решение.
Решите УЧП путем выбора Solve> Solve PDE или нажатия кнопки = на панели инструментов. Приложение время от времени решает уравнение тепла от 0 до 5 секунд и отображает результат в конце отрезка времени.
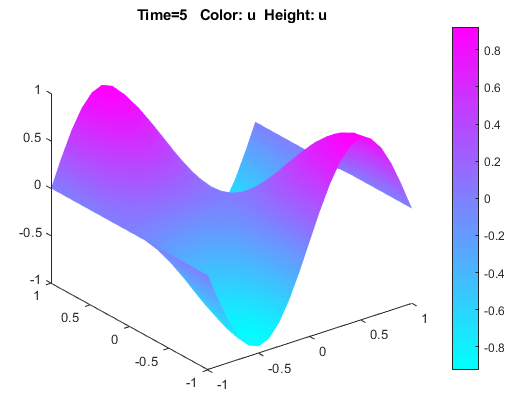
Визуализируйте решение как 3-D помехи и анимированные графики. Для этого:
Выберите Plot> Parameters.
В получившемся диалоговом окне выберите опции Height (3-D plot) и Color.
Чтобы визуализировать динамическое поведение волны, выберите Animation в том же диалоговом окне. Если прогресс анимации является слишком медленным, выберите опцию Plot in x-y grid. x-y сетка может значительно ускорить процесс анимации.