Для твердых частиц с пользовательскими поперечными сечениями Extruded Solid и блоки Revolved Solid позволяют вам создать более истинные основательные представления, чем более простые формы, такие как Brick Solid, Cylindrical Solid, и Spherical Solid часто позволяет. Используйте их при моделировании твердых частиц, которые имеют произвольные все же постоянные поперечные сечения вперед или об оси. Блоком Extruded Solid может или быть General экструзия или Regular экструзия.
Общая экструзия является линейной разверткой пользовательского поперечного сечения вдоль оси, которая нормальна к плоскости поперечного сечения. Развертка охватывает длину, заданную в диалоговом окне блока Extruded Solid. Поперечное сечение может иметь произвольную схему и один или несколько полых разделов — хотя правила для определения поперечных сечений отличаются немного, когда отверстия присутствуют.
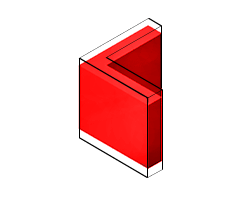
Общие примеры экструзии включают прямые лучи, пластины, штанги, распорки и стержни. Рисунок показывает угловой луч, общая экструзия, поперечное сечение которой состоит из двух тонких прямоугольников, расположенных в форме L. Блок Extruded Solid развертывает форму L линейно из плоскости поперечного сечения, чтобы получить итоговую геометрию луча.
Общий блок Extruded Solid как линейная развертка
Примечание по Формам Extruded Solid. Блок Extruded Solid обеспечивает вторую форму экструзии, названную Regular экструзия. Эта форма является более простой версией General экструзия и подходит только для твердых частиц, поперечные сечения которых являются правильными многоугольниками — те со сторонами той же длины. Схема поперечного сечения фиксируется количеством сторон многоугольника, и это не может содержать отверстия.
Используйте блок Revolved Solid, чтобы сделать угловую развертку поперечного сечения об оси, которая находится на той же плоскости как поперечное сечение. Развертка может охватить полный оборот или меньший угол между 0 и 360 степени. Как с вытесненными формами, поперечное сечение может иметь произвольную схему с или без отверстий.
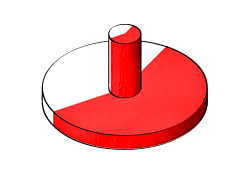
Вращаемые примеры включают конусы, купола, поршни, валы механизма и повороты русла трубопровода. Рисунок показывает цилиндрический штепсель, Revolved Solid, поперечное сечение которого, как угловой луч, состоит из двух тонких прямоугольников, расположенных в форме L. Блок Revolved Solid развертывает форму L об оси, лежащей на плоскости поперечного сечения, чтобы получить итоговую геометрию штепселя.
Revolved Solid как угловая развертка
Вы задаете поперечные сечения численно как матрицы MATLAB, заполненные с координатными парами избранных точек поперечного сечения. Каждая строка матрицы обеспечивает координатную пару для одной точки. Нет никакой верхней границы на количестве строк координатной матрицы, но минимум три требуется, чтобы полностью задавать закрытую форму.
% Coordinate Matrix Example: % Square Cross-Section with Center at [0, 0] and Side Length 2 [ -1 -1; % Lower left corner 1 -1; % Lower right corner 1 1; % Upper right corner -1 1; % Upper left corner ]
Координатные пары обработаны как (x, y) значения в случае вытесненных форм и как (x, z) значения — заданный в том порядке — в случае вращаемых форм. Координаты разрешены в системе координат блока Extruded Solid или Revolved Solid, с (0, 0) пара, совпадающая с источником той системы координат. Это - установившаяся практика к параметрированному координаты в терминах переменных MATLAB, сопоставленных с ключевыми размерами твёрдых тел — например, радиус или длина.
Координатные пары соединяются последовательно в порядке, неявном в координатной матрице. Связи посредством сегментов прямой линии. Результатом является закрытая ломаная линия, которая разделяет область, чтобы быть заполненной материалом (твердая часть) из области, которую оставят полой (любые отверстия, которые могут присутствовать и пустая среда).
Контур между этими двумя областями таков, что, когда вы продолжаете вдоль ломаной линии от одной точки до следующего, твердая область лжет вашему левому и полой области с правой стороны от вас. Первые и последние координатные пары часто являются тем же самым, но если они не, линия связи вставляется между ними, чтобы гарантировать, что поперечное сечение на самом деле закрывается. Анимированный рисунок показывает рисунок бинарного поперечного сечения ссылки без отверстий.

Обратите внимание на то, что поперечное сечение недопустимо, если в какой-либо точке ломаная линия пересекает себя. Однако это хорошо для двух линейных сегментов, чтобы быть произвольно близким или даже совпадающим друг с другом. На самом деле можно использовать это свойство задать поперечное сечение, которое имеет одно или несколько отверстий.
Матрицы координаты Revolved Solid подвергаются специальному ограничению: x - координаты не могут быть отрицательными. Это правило следует частично от оси оборота (z), используемый блоком Revolved Solid. При развертке поперечного сечения любые области слева от этой оси (те с отрицательным x - координаты) становятся перекрытыми с теми направо (положительный x), приведении к неожиданной геометрии тела. Чтобы предотвратить эту проблему, ошибка выпущена, если поперечное сечение Revolved Solid найдено с отрицательным x - координаты.
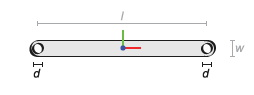
Считайте поперечное сечение показанным на рисунке. Это поперечное сечение принадлежит бинарной ссылке с круглыми концами и никакими отверстиями. Параметрируйте поперечное сечение в терминах показанных размерностей и задайте его в форме координатной матрицы.
Бинарное поперечное сечение ссылки (никакие отверстия)
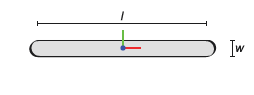
Запустите путем открытия нового скрипта MATLAB и сохраните его в удобном месте под именем modelParams. Добавьте две переменные для показанных на рисунке размерностей, длина (l) и ширина (w). Установите длину на 20 и ширина к 2 (в том, что позже будет модулями cm).
l = 20;
w = 2; Задайте круглые концы как полукруги. Во-первых, сгенерируйте два массива с угловыми промежутками левых и правых концов. Эти массивы позволяют вам параметрировать (xY) координаты с помощью простых тригонометрических выражений. Каждый массив имеет пять точек, но для более сглаженных форм можно задать больше. Транспонировать символ (') гарантирует тот A и B массивы столбца.
A = linspace(-pi/2, pi/2, 5)';
B = linspace(pi/2, 3*pi/2, 5)';Задайте координатные матрицы правильного конца (csRight) и оставленный конец (csLeft). Первый столбец каждой матрицы соответствует x - координата. Второй столбец соответствует y - координата. x - координаты двух концов возмещены в противоположных направлениях l/2.
csRight = [l/2 + w/2*cos(A) w/2*sin(A)];
csLeft = [-l/2 + w/2*cos(B) w/2*sin(B)];Объедините координатные матрицы в одну матрицу под названием cs. Это - матрица, которую необходимо задать в параметре Cross-Section блока Revolved Solid. Обратите внимание на то, что прямые сегменты поперечного сечения автоматически сгенерированы, когда конечные точки полукругов соединяются.
cs = [csRight; csLeft];Можно визуализировать схему поперечного сечения с помощью MATLAB®
plot команда. Введите код, показанный ниже в командной строке MATLAB.
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
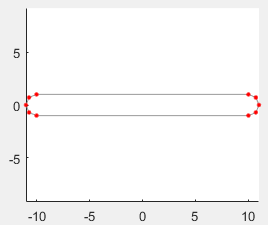
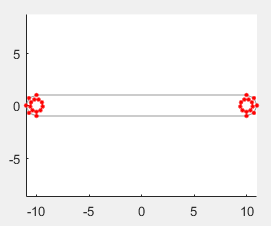
График показывает поперечное сечение бинарной ссылки. Точки в координатной матрице показываются красными точками. Получившаяся схема поперечного сечения показывается светло-серой линией. Заметьте, что конец разделяет, каждый включает пять точек — номер, заданный в угловых массивах промежутка.
Координатная матрица должна всегда представлять один непрерывный путь. Это правило работает хорошо при определении поперечного сечения без отверстий, но оно требует дополнительного ухода, когда отверстия существуют. Поскольку схема отверстия не непрерывна со схемой поперечного сечения, необходимо теперь добавить тонкое сокращение между двумя. Сокращение позволяет вам пересечь поперечное сечение и основы отверстия в одном цикле.
Рассмотрите бинарную ссылку с отверстием в одном конце. Поперечное сечение этого тела включает два замкнутых пути — один для схемы поперечного сечения, другого для отверстия. Пути физически разделяются. Однако можно соединить их путем сокращения каждого пути в вершине и присоединения вершин сокращения с дополнительными линейными сегментами. Анимированный рисунок показывает рисунок бинарного поперечного сечения ссылки с одним отверстием.

Можно расширить этот подход к поперечным сечениям с несколькими отверстиями. Обратите внимание на то, что каждое отверстие должно иметь сокращение. Нет никакого одного лучшего способа приблизиться к сокращениям. Ключ должен запланировать их так, чтобы можно было пересечь поперечное сечение — и все его отверстия — в одном непрерывном пути, мешая ломаной линии пересечь себя. Анимированный рисунок показывает рисунок бинарного поперечного сечения ссылки с двумя отверстиями.

Измените координатную матрицу в своем modelParams скрипт, чтобы включать два идентичных отверстия как показано в фигуру. Сохраняйте скрипт часто, когда вы идете.
Бинарное поперечное сечение ссылки (два отверстия)
Запустите путем добавления новой переменной для диаметра отверстия (d). Установите диаметр на 1.2 (в том, что позже будет модулями cm).
d = 1.2;Сгенерируйте новый угловой массив промежутка для левых и правых отверстий. Отверстия чертятся в том же порядке, и единый массив достаточен. Элементы массива упорядочены в направлении по часовой стрелке, гарантируя, что при генерации поперечного сечения твердая область остается налево. Количество элементов массива удвоилось, чтобы отразить более широкий угловой промежуток отверстий (360 ° по сравнению с 180 °).
C = linspace(3*pi/2, -pi/2, 10)';Задайте основы левого отверстия (csLeftHole), правильное отверстие (csRightHole), и линия связи между двумя (csConnLine). X-координаты переключены оставленные наполовину длина (l/2) для левого отверстия и прямо тем же расстоянием для правильного отверстия.
csLeftHole = [-l/2 + d/2*cos(C) d/2*sin(C)];
csRightHole = [+l/2 + d/2*cos(C) d/2*sin(C)];
csConnLine = [-l/2 -w/2; +l/2 -w/2];Добавьте новые координатные матрицы в существующий cs матрица. Порядок матриц определяет порядок, в котором чертится полное поперечное сечение. Результатом является переменная, которую можно задать в параметре Cross-section блока Revolved Solid.
cs = [csRight; csLeft; csLeftHole; ...
csConnLine; csRightHole];Как прежде, можно визуализировать схему поперечного сечения с помощью MATLAB plot команда. Убедитесь, что код графического вывода, показанный ниже, включен в ваш скрипт. Затем запустите скрипт, чтобы сгенерировать график.
figure; hold on; axis equal; plot(cs(:,1), cs(:,2), 'Color', [0.6 0.6 0.6], 'Marker', '.',... 'MarkerSize', 9, 'MarkerEdgeColor', [1 0 0]);
График показывает поперечное сечение бинарной ссылки. Точки в координатной матрице показываются красными точками. Получившаяся схема поперечного сечения показывается светло-серой линией. Обратите внимание на то, что отверстие разделяет, каждый включает десять точек — номер, заданный в угловых массивах промежутка.
z - ось системы координат служит осью развертки и в Extruded Solid и в блоках Revolved Solid. Заданное поперечное сечение развертывается вдоль этой оси в случае блока Extruded Solid и об этой оси в случае блока Revolved Solid. Развертка симметрична относительно плоскости поперечного сечения: это запускает половину длины развертки или угла в каждом направлении оси развертки. Эта симметрия оставляет плоскость поперечного сечения — и поэтому источник системы координат — на полпути между концами развертки.
Откройте новую модель Simulink® и, от библиотеки Bodies, добавьте блок Extruded Solid. Можно кликнуть по холсту модели, ввести имя блока и сделать выбор из показавших вариантов. Сохраните модель в удобном месте как binaryLinkSolid.
В диалоговом окне блока Extruded Solid, установленном параметры Geometry как показано в таблице. Установите модули параметра на cm. Параметр Cross-Section задан в терминах cs переменная в вашем modelParams скрипт.
| Параметр | Значение |
|---|---|
| Cross-Section | cs |
| Length | 1 |
Загрузите свой modelParams скрипт к вашему рабочему пространству модели:
Во вкладке Modeling нажмите Model Explorer. Вы используете этот инструмент, чтобы загрузить modelParams скрипт, который вы ранее создали на свое рабочее пространство модели.
В панели Model Hierarchy расширьте узел, соответствующий вашей модели (binaryLinkSolid), и выберите Model Workspace.
В панели Model Workspace, установленной параметр Data source на MATLAB File и просмотрите свой modelParams скрипт. Нажмите кнопку Reinitialize from Source, чтобы загрузить переменные, заданные в скрипте.
В диалоговом окне блока Extruded Solid нажмите кнопку Update Visualization![]() . Панель визуализации обновляется с итоговой геометрией тела.
. Панель визуализации обновляется с итоговой геометрией тела.
Нажмите кнопку Fit to View, чтобы масштабировать бинарную ссылку на размер панели визуализации. Нажмите кнопку Toggle visibility of frames, чтобы показать твердую систему координат. Источник системы координат совпадает с [0, 0], поперечное сечение координирует, и находится на полпути между концами экструзии.
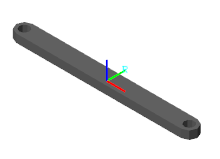
Отметьте зубчатый внешний вид круглых концов и отверстий. Этот эффект следует из маленького числа точек, используемого в круглых фрагментах координатной матрицы — csLeftEnd, csRightEnd, csLeftHole, и csRightHole. Увеличьте число элементов в угловых массивах промежутка, чтобы получить более сглаженную геометрию.