Exponenta Banner

bearingFaultBands

Сгенерируйте диапазоны частот вокруг характеристических частот отказа шарикоподшипников или роликовых подшипников для спектрального извлечения признаков

свернуть все на странице

Синтаксис

FB = bearingFaultBands(FR,NB,DB,DP,beta)
FB = bearingFaultBands(___,Name,Value)
[FB,info] = bearingFaultBands(___)
bearingFaultBands(___)

Описание

пример

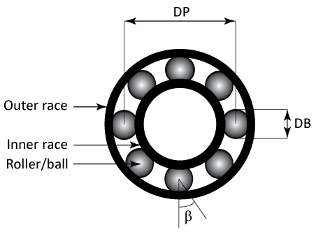
FB = bearingFaultBands(FR,NB,DB,DP,beta) генерирует характеристические диапазоны частот отказа FB из ролика или шарикоподшипника с помощью его физических параметров. FR скорость вращения вала или внутренней гонки, NB количество мячей или роликов, DB мяч или диаметр ролика, DP диаметр тангажа и beta угол контакта в градусах. Значения в FB имейте те же неявные модули как FR.

пример

FB = bearingFaultBands(___,Name,Value) позволяет вам задавать дополнительные параметры с помощью одного или нескольких аргументов пары "имя-значение".

пример

[FB,info] = bearingFaultBands(___) также возвращает структуру info содержа информацию о сгенерированных диапазонах частот отказа FB.

пример

bearingFaultBands(___) без выходных аргументов строит столбчатую диаграмму сгенерированных диапазонов частот отказа FB.

Примеры

свернуть все

Скрипт Open Live Script

В данном примере рассмотрите терпение диаметра тангажа 12 см с восемью прокручивающимися элементами. Каждое тело качения имеет диаметр 2 см. Внешняя гонка остается стационарной, когда внутренняя гонка управляется на уровне 25 Гц. Угол контакта прокручивающегося элемента является 15 градусами.

С вышеупомянутыми физическими размерностями подшипника создайте диапазоны частот с помощью bearingFaultBands.

FR = 25;
NB = 8;
DB = 2;
DP = 12;
beta = 15;
FB = bearingFaultBands(FR,NB,DB,DP,beta)
FB = 4×2

   82.6512   85.1512
  114.8488  117.3488
   71.8062   74.3062
    9.2377   11.7377

FB возвращен как 4x2 массив с шириной диапазона частот по умолчанию 10 процентов FR который составляет 2,5 Гц. Первый столбец в FB содержит значения F-W2, в то время как второй столбец содержит все значения F+W2 для каждой характеристической дефектной частоты.

Скрипт Open Live Script

В данном примере рассмотрите микро роликовый подшипник с 11 роликами, где каждый ролик составляет 7,5 мм. Диаметр тангажа составляет 34 мм, и угол контакта является 0 градусами. При принятии скорости вала 1 800 об/мин создайте диапазоны частот для роликового подшипника. Задайте 'Domain'как 'frequency'чтобы получить диапазоны частот FB в тех же модулях как FR.

FR = 1800;
NB = 11;
DB = 7.5;
DP = 34;
beta = 0;
[FB1,info1] = bearingFaultBands(FR,NB,DB,DP,beta,'Domain','frequency')
FB1 = 4×2
104 ×

    0.7626    0.7806
    1.1994    1.2174
    0.3791    0.3971
    0.0611    0.0791


info1 = struct with fields:
        Centers: [7.7162e+03 1.2084e+04 3.8815e+03 701.4706]
         Labels: ["1Fo"    "1Fi"    "1Fb"    "1Fc"]
    FaultGroups: [1 2 3 4]

Теперь включайте боковые полосы для внутренней гонки и прокручивающихся частот дефекта элемента с помощью 'Sidebands'пара "имя-значение".

[FB2,info2] = bearingFaultBands(FR,NB,DB,DP,beta,'Domain','order','Sidebands',0:1)
FB2 = 8×2

    4.2368    4.3368
    5.6632    5.7632
    6.6632    6.7632
    7.6632    7.7632
    1.7167    1.8167
    2.1064    2.2064
    2.4961    2.5961
    0.3397    0.4397


info2 = struct with fields:
        Centers: [4.2868 5.7132 6.7132 7.7132 1.7667 2.1564 2.5461 0.3897]
         Labels: [1x8 string]
    FaultGroups: [1 2 2 2 3 3 3 4]

Можно использовать сгенерированные полосы FB отказа извлекать спектральные метрики с помощью faultBandMetrics команда.

Скрипт Open Live Script

В данном примере рассмотрите поврежденное терпение диаметра тангажа 12 см с восемью прокручивающимися элементами. Каждое тело качения имеет диаметр 2 см. Внешняя гонка остается стационарной, когда внутренняя гонка управляется на уровне 25 Гц. Угол контакта прокручивающегося элемента является 15 градусами.

С вышеупомянутыми физическими размерностями подшипника визуализируйте диапазоны частот отказа с помощью bearingFaultBands.

FR = 25;
NB = 8;
DB = 2;
DP = 12;
beta = 15;
bearingFaultBands(FR,NB,DB,DP,beta)

Figure contains an axes. The axes with title Fault Frequency Bands contains 8 objects of type patch, text.

Из графика наблюдайте следующие переносящие определенные частоты вибрации:

  • Частота дефекта клетки, Fc на уровне 10,5 Гц.

  • Частота дефекта мяча, Fb на уровне 73 Гц.

  • Внешняя частота дефекта гонки, Fo на уровне 83,9 Гц.

  • Внутренняя частота дефекта гонки, Fi на уровне 116,1 Гц.

Скрипт Open Live Script

В данном примере рассмотрите шарикоподшипник с диаметром тангажа 12 см с 10 прокручивающимися элементами. Каждый элемент прокрутки имеет диаметр 0,5 см. Внешняя гонка остается стационарной, когда внутренняя гонка управляется на уровне 25 Гц. Угол контакта мяча является 0 градусами. Набор данных bearingData.mat содержит степень спектральную плотность (PSD) и ее соответствующие данные о частоте для сигнала вибрации подшипника в таблице.

Во-первых, создайте диапазоны частот подшипника включая первые 3 боковых полосы с помощью физических характеристик шарикоподшипника.

FR = 25;
NB = 10;
DB = 0.5;
DP = 12;
beta = 0;
FB = bearingFaultBands(FR,NB,DB,DP,beta,'Sidebands',1:3)
FB = 14×2

  118.5417  121.0417
   53.9583   56.4583
   78.9583   81.4583
  103.9583  106.4583
  153.9583  156.4583
  178.9583  181.4583
  203.9583  206.4583
  262.2917  264.7917
  274.2708  276.7708
  286.2500  288.7500
      ⋮

FB 14x2 массив, который включает первичные частоты и их боковые полосы.

Загрузите данные PSD. bearingData.mat содержит таблицу X где PSD содержится в первом столбце, и сетка частоты находится во втором столбце как массивы ячеек соответственно.

load('bearingData.mat','X')
X
X=1×2 table
          Var1                Var2      
    ________________    ________________

    {12001x1 double}    {12001x1 double}

Вычислите спектральные метрики с помощью данных PSD в таблице X и диапазоны частот в FB.

spectralMetrics = faultBandMetrics(X,FB)
spectralMetrics=1×43 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

         121               121            314.43          56.438            56.438          144.95          81.438            81.438          210.57          106.44            106.44          276.2           156.44            156.44          407.45          181.44            181.44          473.07          206.44            206.44          538.7           264.75            264.75          691.77          276.75            276.75          723.27          288.69             288.69           754.61           312.69             312.69           817.61           324.62             324.62           848.94           336.62             336.62           880.44           13.188             13.188           31.418           7113.4

spectralMetrics 1x43 таблица с пиковой амплитудой, пиковой частотой и мощностью полосы, вычисленной для каждого частотного диапазона в FB. Последний столбец в spectralMetrics общая мощность полосы, вычисленная через все 14 частот в FB.

Входные параметры

свернуть все

Скорость вращения вала или внутренней гонки в виде положительной скалярной величины. FR основная частота вокруг который bearingFaultBands генерирует диапазоны частот отказа. Задайте FR или в Герц или в оборотах в минуту.

Количество мячей или роликов в подшипнике в виде положительного целого числа.

Диаметр мяча или ролика в виде положительного целого числа.

Передайте диаметр подшипника в виде положительной скалярной величины. DP диаметр круга, что центр мяча или ролика перемещается во время вращения подшипника.

Свяжитесь с углом в градусах между плоским перпендикуляром к мячу или оси ролика и линией, соединяющей эти два кабелепровода в виде положительной скалярной величины.

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: ...,'Harmonics',[1,3,5]

Гармоники основной частоты, которая будет включена в виде разделенной запятой пары, состоящей из 'Harmonics'и вектор из положительных целых чисел. Значение по умолчанию равняется 1. Задайте 'Harmonics'когда это необходимо, чтобы создать диапазоны частот с большим количеством гармоник основной частоты.

Боковые полосы вокруг основной частоты и ее гармоник, которые будут включены в виде разделенной запятой пары, состоящей из 'Sidebands'и вектор из неотрицательных целых чисел. Значение по умолчанию 0. Задайте 'Sidebands'когда это необходимо, чтобы создать диапазоны частот с боковыми полосами вокруг основной частоты и ее гармоник.

Ширина диапазонов частот, сосредоточенных на номинальных частотах отказа в виде разделенной запятой пары, состоящей из 'Width'и положительная скалярная величина. Значение по умолчанию составляет 10 процентов основной частоты. Постарайтесь не задавать 'Width'с большим значением так, чтобы полосы отказа не перекрывались.

Единицы частот полосы отказа в виде разделенной запятой пары, состоящей из 'Domain'и любой 'frequency' или 'order'. Выбор:

  • 'frequency' если вы хотите FB быть возвращенным в тех же модулях как FR.

  • 'order' если вы хотите FB быть возвращенным как количество вращений относительно внутреннего вращения гонки, FR.

Выходные аргументы

свернуть все

Диапазоны частот отказа, возвращенные как Nx2 массив, где N количество частот отказа. FB возвращен в тех же модулях как FR, или в герц или в порядках в зависимости от значения 'Domain'. Используйте сгенерированные диапазоны частот отказа, чтобы извлечь спектральное метрическое использование faultBandMetrics. Сгенерированные полосы отказа, [F−W2, F+W2], сосредоточены в:

  • Внешняя частота дефекта гонки, Fo и его гармоники

  • Внутренняя частота дефекта гонки, Fi, его гармоники и боковые полосы в FR

  • Прокручивая элемент (мяч) частота дефекта, Fbего гармоники и боковые полосы в Fc

  • Клетка (обучает) дефектную частоту, Fc и его гармоники

Значение W ширина диапазонов частот, которые можно задать использование 'Width'пара "имя-значение". Для получения дополнительной информации о подшипнике частот см. Алгоритмы.

Информация о диапазонах частот отказа в FB, возвращенный как структура со следующими полями:

  • Centers — Центральные частоты отказа

  • Labels — Метки, описывающие каждую частоту

  • FaultGroups — Числа группы отказа, идентифицирующие связанные частоты отказа

Алгоритмы

bearingFaultBands вычисляет различные характеристические частоты подшипника можно следующим образом:

  • Внешняя частота дефекта гонки, Fo=NB2FR(1−DBDPпотому что(β))

  • Внутренняя частота дефекта гонки, Fi=NB2FR(1+DBDPпотому что(β))

  • Прокрутка элемента (мяч) частота дефекта, Fb=DP2DBFR(1−[DBDPпотому что(β)]2)

  • Клетка (обучает) дефектную частоту,Fc=FR2(1−DBDPпотому что(β))

Ссылки

[1] Chandravanshi, M & Poddar, Surojit. "Обнаружение отказа шарикоподшипника Используя параметры вибрации". Международный журнал Engineering Research & Technology. 2. 2013.

[2] Singh, Sukhjeet & Kumar, Amit & Kumar, Навин. "Моторный текущий анализ подписи для подшипника обнаружения отказа в механических системах". Procedia Materials Science. 6. 171–177. 10.1016/j.mspro.2014.07.021. 2014.

[3] Roque, Antonio & Silva, Tiago & Calado, João & Dias, J. "Подход к диагностике отказа прокручивающихся подшипников". Транзакции WSEAS в Системах и Управлении. 4. 2009.

Смотрите также

| |

Введенный в R2019b

Документация Predictive Maintenance Toolbox

Поддержка