mdlProjection

Встревожьте решение решателя состояний системы лучше удовлетворить независимым от времени отношениям решения

Необходимый

Нет

Языки

C, C++

Синтаксис

#define MDL_PROJECTION
void mdlProjection(SimStruct *S)

Аргументы

S: SimStruct, представляющий Блок s-function.

Описание

Этот метод предназначается для использования с S-функциями, что динамические системы модели, состояния которых удовлетворяют независимым от времени отношениям, таким как те, которые следуют из массы или энергосбережения или других физических законов. Механизм Simulink^® вызывает этот метод на каждом временном шаге после того, как решатель модели вычислил состояния S-функции для того временного шага. Как правило, небольшие ошибки в числовом решении состояний вызывают решения не удаться удовлетворить инвариантам решения точно. Ваш mdlProjection метод может компенсировать ошибки путем беспокойства состояний так, чтобы они более тесно инварианты приближенного решения на шаге текущего времени. В результате числовое решение придерживается более тесно идеального решения, в то время как симуляция прогрессирует, производя более точную полную симуляцию системы, смоделированной вашей S-функцией.

Ваш mdlProjection возмущения метода системных состояний должны находиться в пределах ошибочных допусков решения, заданных моделью, в которую встраивается S-функция. В противном случае возмущения могут делать недействительным решение решателя. Это до вашего mdlProjection метод, чтобы гарантировать, что возмущения соответствуют ошибочным допускам, заданным моделью. Смотрите Беспокойство состояний Системы Используя Инвариант Решения для простого метода для беспокойства состояний системы. Следующие статьи описывают более сложные методы возмущения что ваш mdlProjection метод может использовать.

C.W. Механизм, “Обеспечивая инварианты решения в числовом решении ОДУ”, журнал на научном и статистическом вычислении, издании 7, № 3, июль 1986.
Л.Ф. Шемпин, “Законы сохранения и Числовое Решение ОДУ I”, Компьютеры и Математика с Приложениями, Изданием 12B, 1986, стр 1287–1296.
Л.Ф. Шемпин, “Законы сохранения и Числовое Решение ОДУ II”, Компьютеры и Математика с Приложениями, Изданием 38, 1999, стр 61–72.

Пример

Беспокойство состояний системы Используя инвариант решения

Вот простой, Основанный на ряде Тейлора подход к беспокойству состояний системы. Предположим свои S-модели-функции динамическая система, имеющая инвариант решения, $g (X, t)$ т.е. . $g$ непрерывная, дифференцируемая функция системных состояний, $X$ , и время, $t$ , чье значение является постоянным со временем. То

$X_{n} ≅ X_{n}^{*} + J_{n}^{T} {(J_{n} J_{n}^{T})}^{- 1} R_{n}$

где

$X_{n}$ идеальный вектор состояния системы на шаге текущего времени решателя
$X_{n}^{*}$ аппроксимированный вектор состояния, вычисленный решателем на шаге текущего времени
$J_{n}$ якобиан инвариантной функции, выполненной в точке в пространстве состояний, заданном аппроксимированным вектором состояния на шаге текущего времени:
$J_{n} = \frac{\partial g}{\partial X} (X_{n}^{*}, t_{n})$
$t_{n}$ время на шаге текущего времени
$R_{n}$ невязка (различие) между инвариантной функцией, выполненной в $X_{n}$ и $X_{n}^{*}$ на шаге текущего времени:
$R_{n} = g (X_{n}, t_{n}) - g (X_{n}^{*}, t_{n})$
Примечание
Значение $g (X_{n}, t_{n})$ то же самое на каждом временном шаге и известно по определению.

Учитывая непрерывную, дифференцируемую инвариантную функцию для системы, что ваши S-модели-функции, эта формула позволяет mdlProjection вашей S-функции метод, чтобы вычислить возмущение

$J_{n}^{T} {(J_{n} J_{n}^{T})}^{- 1} R_{n}$

из числового решения решателя, $X_{n}^{*}$ , это более тесно совпадает с идеальным решением, $X_{n}$ , мешать решению S-функции дрейфовать от идеального решения как симуляция прогрессирует.

Пример MATLAB

Этот пример иллюстрирует, как метод возмущения, обрисованный в общих чертах в предыдущем разделе, может помешать числовому решению модели дрейфовать от идеального решения, в то время как симуляция прогрессирует. Рассмотрите следующую модель, mdlProjectionEx1:

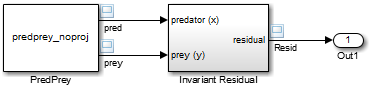
Блок PredPrey ссылается на S-функцию, которая использует уравнения Lotka-Volterra:

predprey_noproj.m

function predprey_noproj(block)
% This is one of a pair S-functions that model a population of predators
% and preys, the other being predprey.m.

% Both S-functions use the Lotka-Volterra equations
%
%   xdot = ax(1-y)
%   ydot = -cy(1-x)
%
% to model changes in the population where x(t) and y(t) are 
% the number of predators and prey, respectively, and 
% a and c are constants. Both S-functions assume a=1 and c=2 and
% that the population consists initially of one predator and three prey.
% 
% The solution to the Lotka-Volterra equations obeys the time-invariant
% relationship
%
%   (x^-c)*exp(cx)*(y^-a)*exp(ay) = d
%
% where d is a constant.
%
% The other S-function uses this relationship to compensate for
% numerical errors in the solver's solution of the model's state
% equations. This S-function does not attempt to compensate for the
% numerical errors. As a result, the solution drifts from the ideal
% solution as the simulation progresses.
%
% For more information, see the documentation for the mdlProjection 
% method in the online Simulink documentation.
%   
% Copyright 2006 The MathWorks, Inc.

  setup(block);
  
%endfunction

function setup(block)
  
  %% Register number of input and output ports
  block.NumInputPorts  = 0;
  block.NumOutputPorts = 2;

  block.OutputPort(1).Dimensions       = 1;
  block.OutputPort(1).SamplingMode = 'Sample';
  
  block.OutputPort(2).Dimensions       = 1;
  block.OutputPort(2).SamplingMode = 'Sample';

  
  %% Set block sample time to variable sample time
  block.SampleTimes = [0 0];
  
  %% Setup Dwork
  block.NumContStates = 2;
  
  %% Register methods
  block.RegBlockMethod('InitializeConditions',    @InitConditions); 
  block.RegBlockMethod('Outputs',                 @Output);  
  block.RegBlockMethod('Derivatives', @Derivatives);
  block.RegBlockMethod('Projection', @Projection);
  block.RegBlockMethod('Update', @Update);
  
%endfunction

function InitConditions(block)

  %% Initialize Dwork: 1 predator, 3 prey.
  block.ContStates.Data = [1 3]';
  
  
%endfunction

function Output(block)

  % Output number of predators.
  block.OutputPort(1).Data = block.ContStates.Data(1);
  
  % Output number of prey.
  block.OutputPort(2).Data = block.ContStates.Data(2);
  
  block.ContStates.Data;
  
%endfunction

function Derivatives(block)

states = block.ContStates.Data;
% System ODEs
block.Derivatives.Data = [2*states(1)*(1-states(2)); -states(2)*(1-states(1))];
  
%endfunction

function Projection(block)
    %not implemented
%endfunction

function Update(block)

%endfunction

$\begin{array}{l} \dot{x} = a x (1 - y) \\ \dot{y} = - c y (1 - x) \end{array}$

к динамике популяции жертв хищника модели, где $x (t)$ плотность населения хищников и $y (t)$ плотность населения добычи. Идеальное решение ОДУ добычи хищника удовлетворяет независимой от времени функции

$x^{- c} e^{c x} y^{- a} e^{a y} = d$

где $a$ , $c$ , и $d$ константы. S-функция принимает a = 1, c = 2, и d = 121.85.

Блок Invariant Residual в этой модели вычисляет невязку между инвариантной функцией, выполненной вдоль идеальной траектории системы через пространство состояний и его симулированной траекторией:

$R_{n} = d - x_{n}^{- c} e^{c x_{n}} y_{n}^{- a} e^{a y_{n}}$

где $x_{n}$ и $y_{n}$ значения, вычисленные решателем модели для хищника и плотности популяции жертв, соответственно, на шаге текущего времени. Идеально, невязка должна быть нулем в течение симуляции модели, но симуляция модели показывает, что невязка на самом деле значительно отклоняется от нуля:

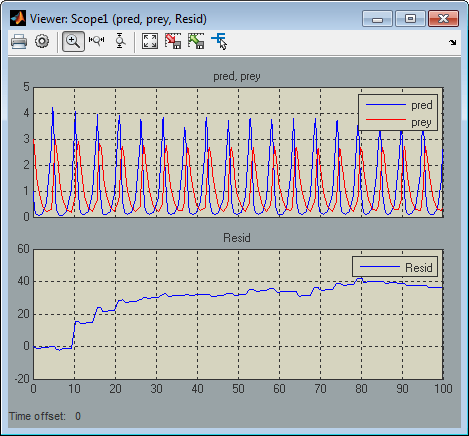
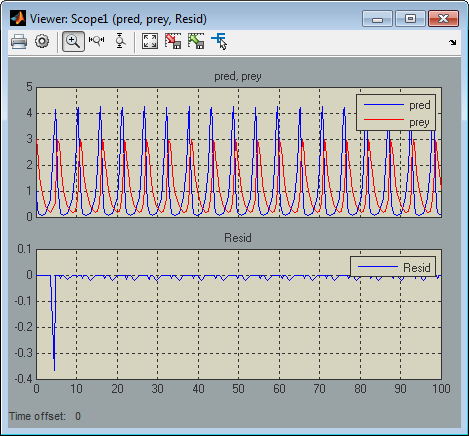
Теперь рассмотрите следующую модель, mdlProjectionEx2:

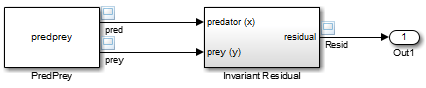
Эта модель совпадает с предыдущей моделью, за исключением того, что ее S-функция, predprey.m, включает mdlProjection метод, который использует подход возмущения, обрисованный в общих чертах в Беспокойстве состояний Системы Используя Инвариант Решения, чтобы компенсировать числовой дрейф. В результате числовое решение более тесно отслеживает идеальное решение, в то время как симуляция прогрессирует, как продемонстрировано остаточным сигналом, который остается рядом или в нуле в течение симуляции:

predprey.m

function predprey(block)
% This is one of a pair S-functions that model a population of predators
% and preys, the other being predprey_noproj.m.

% Both S-functions use the Lotka-Volterra equations
%
%   xdot = ax(1-y)
%   ydot = -cy(1-x)
%
% to model changes in the population where x(t) and y(t) are 
% the number of predators and prey, respectively, and 
% a and c are constants. Both S-functions assume a=1 and c=2 and
% that the population consists initially of one predator and three prey.
% 
% The solution to the Lotka-Volterra equations obeys the time-invariant
% relationship
%
%   (x^-c)*exp(cx)*(y^-a)*exp(ay) = d
%
% where d is a constant.
%
% This S-function uses this relationship to compensate for
% numerical errors in the solver's solution of the model's state
% equations. The other S-function does not. As a result, 
% the other's solution drifts from the ideal solution as the 
% simulation progresses.
%
% For more information, see the documentation for the mdlProjection 
% method in the online Simulink documentation.
%   
% Copyright 2006 The MathWorks, Inc.
  setup(block);
  
%endfunction

function setup(block)
  
  %% Register number of input and output ports
  block.NumInputPorts  = 0;
  block.NumOutputPorts = 2;

  block.OutputPort(1).Dimensions       = 1;
  block.OutputPort(1).SamplingMode = 'Sample';
  
  block.OutputPort(2).Dimensions       = 1;
  block.OutputPort(2).SamplingMode = 'Sample';

  
  %% Set block sample time to variable sample time
  block.SampleTimes = [0 0];
  
  %% Setup Dwork
  block.NumContStates = 2;
  
  %% Register methods
  block.RegBlockMethod('InitializeConditions',    @InitConditions); 
  block.RegBlockMethod('Outputs',                 @Output);  
  block.RegBlockMethod('Derivatives', @Derivatives);
  block.RegBlockMethod('Projection', @Projection);
  
%endfunction

function InitConditions(block)

  %% Initialize Dwork: 1 predator, 3 prey.
  block.ContStates.Data = [1 3]';
  
  
%endfunction

function Output(block)

  % Output number of predators.
  block.OutputPort(1).Data = block.ContStates.Data(1);
  
  % Output number of prey.
  block.OutputPort(2).Data = block.ContStates.Data(2);
  block.ContStates.Data;
  
%endfunction

function Derivatives(block)

states = block.ContStates.Data;
% System ODEs
block.Derivatives.Data = [2*states(1)*(1-states(2)); -states(2)*(1-states(1))];
  
%endfunction

function Projection(block)

states = block.ContStates.Data;

%Computing the Jacobian of the Invariant
J = localInvJac(states);

%Computing the residual of the invariant
R = localInvRes(states);

%Perturbing the states
states = states + (J')*((J*(J'))^-1) * R;

%Update the states
block.ContStates.Data = states; 

%endfunction

function J = localInvJac(states)

%Computing the Jacobian of the invariant
L = 1/states(1) * exp(states(1));
R = 1/(states(2)^2)*exp(2*states(2));
Lx = (states(1)-1)/(states(1)^2)*exp(states(1));
Ry = 2*(states(2)-1)/(states(2)^3)*exp(2*states(2));

J = [Lx*R L*Ry];

%endfunction

function R = localInvRes(states)

%Invariant value
inv0 = 1.218481287142732e+002;

%Computing invariant
L = 1/states(1) * exp(states(1));
R = 1/(states(2)^2)*exp(2*states(2));
inv = L*R;

%Residual
R = inv0-inv;

%endfunction

Смотрите также

Projection

Представленный в R2006b

Документация