Пакет: sdo.requirements
Суперклассы:
Наложите эллиптический, привязал траекторию плоскости фазы двух сигналов
Используйте sdo.requirements.PhasePlaneEllipse объект наложить эллиптическое привязал траекторию плоскости фазы двух сигналов в модели Simulink®. Траектория плоскости фазы является графиком двух сигналов друг против друга. Вы задаете радиусы, центр и вращение эллипса ограничения. Вы также задаете, требуете ли вы траектории двух сигналов лечь внутри или снаружи эллипса.
Следующее изображение показывает эллипс ограничения и пример траектории плоскости фазы двух сигналов.
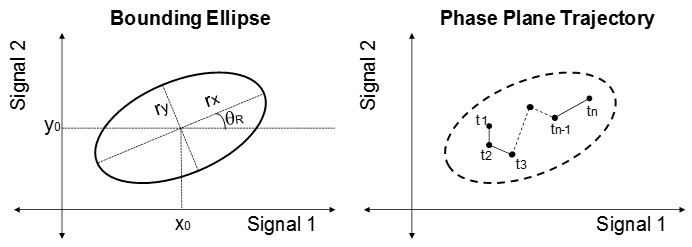
Плоскость X-Y является плоскостью фазы, заданной двумя сигналами. rx и ry являются радиусами эллипса ограничения вдоль x и осей y, и θR является вращением эллипса о центре. Центр эллипса в (x0, y0). В изображении траектория плоскости фазы сигналов находится в эллипсе ограничения для всех моментов времени t1 к tn.
Можно использовать объект в качестве входа к функции стоимости и использовать evalRequirement команда в функции стоимости, чтобы оценить, удовлетворяют ли ваши тестовые сигналы заданному требованию. Можно затем использовать функцию стоимости и sdo.optimize выполнять оптимизацию оценки или ответа параметра согласно удовлетворенности заданного требования. Если вы выполняете анализ чувствительности, после того, как вы генерируете выборки параметра, можно использовать функцию стоимости и sdo.evaluate оценивать требование для каждой сгенерированной выборки.
requirement =
sdo.requirements.PhasePlaneEllipsesdo.requirements.PhasePlaneEllipse объект требования и значения по умолчанию присвоений к его свойствам. Используйте запись через точку, чтобы настроить свойства.
Используйте evalRequirement команда, чтобы оценить, удовлетворяют ли тестовые сигналы заданному требованию.
requirement = sdo.requirements.PhasePlaneEllipse(Name,Value)Name,Value парные аргументы. Name имя свойства и Value соответствующее значение. Name должен появиться в одинарных кавычках (''). Можно задать несколько аргументов пары "имя-значение" в любом порядке как Name1,Value1,...,NameN,ValueN.
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
Используйте Name,Value аргументы, чтобы задать свойства требования возражают во время создания объекта. Например, requirement = sdo.requirements.PhasePlaneEllipse('Type','>=') создает sdo.requirements.PhasePlaneEllipse возразите и задает Type свойство как связанное внешнее.
| evalRequirement | Оцените удовлетворенность эллиптических, привязал траекторию плоскости фазы двух сигналов |
Указатель. Чтобы узнать, как классы Handle влияют на операции копирования, см. раздел "Копирование объектов".
copy | evalRequirement | get | set