loss

Потеря классификации для Гауссовой модели классификации ядер

свернуть все на странице

Синтаксис

L = loss(Mdl,X,Y)

L = loss(Mdl,Tbl,ResponseVarName)

L = loss(Mdl,Tbl,Y)

L = loss(___,Name,Value)

Описание

пример

L = loss(Mdl,X,Y) возвращает потерю классификации для бинарной Гауссовой модели Mdl классификации ядер использование данных о предикторе в X и соответствующий класс помечает в Y.

L = loss(Mdl,Tbl,ResponseVarName) возвращает потерю классификации для модели Mdl использование данных о предикторе в Tbl и истинный класс помечает в Tbl.ResponseVarName.

L = loss(Mdl,Tbl,Y) возвращает потерю классификации для модели Mdl использование данных о предикторе в таблице Tbl и истинный класс помечает в Y.

пример

L = loss(___,Name,Value) задает опции с помощью одного или нескольких аргументов пары "имя-значение" в дополнение к любой из комбинаций входных аргументов в предыдущих синтаксисах. Например, можно задать функцию потерь классификации и веса наблюдения. То, loss возвращает взвешенную потерю классификации с помощью заданной функции потерь.

Примеры

свернуть все

Оцените потерю классификации наборов тестов

Скрипт Open Live Script

Загрузите ionosphere набор данных. Этот набор данных имеет 34 предиктора, и 351 бинарный ответ для радара возвращается, любой плохо ('b') или хороший ('g').

load ionosphere

Разделите набор данных в наборы обучающих данных и наборы тестов. Задайте 15%-ю выборку затяжки для набора тестов.

rng('default') % For reproducibility
Partition = cvpartition(Y,'Holdout',0.15);
trainingInds = training(Partition); % Indices for the training set
testInds = test(Partition); % Indices for the test set

Обучите бинарную модель классификации ядер использование набора обучающих данных.

Mdl = fitckernel(X(trainingInds,:),Y(trainingInds));

Оцените ошибку классификации наборов обучающих данных и ошибку классификации наборов тестов.

ceTrain = loss(Mdl,X(trainingInds,:),Y(trainingInds))

ceTrain = 0.0067

ceTest = loss(Mdl,X(testInds,:),Y(testInds))

ceTest = 0.1140

Задайте пользовательскую потерю классификации

Скрипт Open Live Script

load ionosphere

rng('default') % For reproducibility
Partition = cvpartition(Y,'Holdout',0.15);
trainingInds = training(Partition); % Indices for the training set
testInds = test(Partition); % Indices for the test set

Обучите бинарную модель классификации ядер использование набора обучающих данных.

Mdl = fitckernel(X(trainingInds,:),Y(trainingInds));

Создайте анонимную функцию, которая измеряет линейную потерю, то есть,

$L = \frac{\sum_{j} - w_{j} y_{j} f_{j}}{\sum_{j} w_{j}} .$

$w_{j}$ вес для наблюдения j, $y_{j}$ ответ j (-1 для отрицательного класса, и 1 в противном случае), и $f_{j}$ необработанная классификационная оценка наблюдения j.

linearloss = @(C,S,W,Cost)sum(-W.*sum(S.*C,2))/sum(W);

Пользовательские функции потерь должны быть написаны в конкретной форме. Для правил о записи пользовательской функции потерь смотрите 'LossFun' аргумент пары "имя-значение".

Оцените потерю классификации наборов обучающих данных и потерю классификации наборов тестов с помощью линейной функции потерь.

ceTrain = loss(Mdl,X(trainingInds,:),Y(trainingInds),'LossFun',linearloss)

ceTrain = -1.0851

ceTest = loss(Mdl,X(testInds,:),Y(testInds),'LossFun',linearloss)

ceTest = -0.7821

Входные параметры

свернуть все

`Mdl` — Бинарная модель классификации ядер
`ClassificationKernel` объект модели

Бинарная модель классификации ядер в виде ClassificationKernel объект модели. Можно создать ClassificationKernel использование объекта модели fitckernel.

`X` — Данные о предикторе
n-by-p числовая матрица

Данные о предикторе в виде n-by-p числовая матрица, где n является количеством наблюдений и p, являются количеством предикторов, используемых, чтобы обучить Mdl.

Длина Y и количество наблюдений в X должно быть равным.

Типы данных: single | double

`Y` — Метки класса
категориальный массив | символьный массив | массив строк | логический вектор | числовой вектор | массив ячеек из символьных векторов

Класс помечает в виде категориального, символа или массива строк; логический или числовой вектор; или массив ячеек из символьных векторов.

Тип данных Y должен совпасть с типом данных Mdl.ClassNames. (Программное обеспечение обрабатывает строковые массивы как массивы ячеек из символьных векторов.)
Отличные классы в Y должно быть подмножество Mdl.ClassNames.
Если Y символьный массив, затем каждый элемент должен соответствовать одной строке массива.
Длина Y должно быть равно количеству наблюдений в X или Tbl.

`Tbl` — Выборочные данные
таблица

Выборочные данные раньше обучали модель в виде таблицы. Каждая строка Tbl соответствует одному наблюдению, и каждый столбец соответствует одному переменному предиктору. Опционально, Tbl может содержать дополнительные столбцы для весов наблюдения и переменной отклика. Tbl должен содержать все предикторы, используемые, чтобы обучить Mdl. Многостолбцовые переменные и массивы ячеек кроме массивов ячеек из символьных векторов не позволены.

Если Tbl содержит переменную отклика, используемую, чтобы обучить Mdl, затем вы не должны задавать ResponseVarName или Y.

Если вы обучаете Mdl использование выборочных данных, содержавшихся в таблице, затем входные данные для loss должен также быть в таблице.

`ResponseVarName` — Имя переменной отклика
имя переменной в `Tbl`

Имя переменной отклика в виде имени переменной в Tbl. Если Tbl содержит переменную отклика, используемую, чтобы обучить Mdl, затем вы не должны задавать ResponseVarName.

Если вы задаете ResponseVarName, затем необходимо задать его как вектор символов или строковый скаляр. Например, если переменная отклика хранится как Tbl.Y, затем задайте ResponseVarName как 'Y'. В противном случае программное обеспечение обрабатывает все столбцы Tbl, включая Tbl.Y, как предикторы.

Переменная отклика должна быть категориальным, символом или массивом строк; логический или числовой вектор; или массив ячеек из символьных векторов. Если переменная отклика является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

Типы данных: char | string

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: L = loss(Mdl,X,Y,'LossFun','quadratic','Weights',weights) возвращает взвешенную потерю классификации с помощью квадратичной функции потерь.

`'LossFun'` — Функция потерь
`'classiferror'` (значение по умолчанию) | `'binodeviance'` | `'exponential'` | `'hinge'` | `'logit'` | `'mincost'` | `'quadratic'` | указатель на функцию

Функция потерь в виде разделенной запятой пары, состоящей из 'LossFun' и встроенное имя функции потерь или указатель на функцию.

Эта таблица приводит доступные функции потерь. Задайте тот с помощью его соответствующего значения.

Значение	Описание
`'binodeviance'`	Биномиальное отклонение
`'classiferror'`	Неправильно классифицированный уровень в десятичном числе
`'exponential'`	Экспоненциальная потеря
`'hinge'`	Потеря стержня
`'logit'`	Логистическая потеря
`'mincost'`	Минимальный ожидал стоимость misclassification (для классификационных оценок, которые являются апостериорными вероятностями),
`'quadratic'`	Квадратичная потеря

'mincost' подходит для классификационных оценок, которые являются апостериорными вероятностями. Для моделей классификации ядер ученики логистической регрессии возвращают апостериорные вероятности как классификационные оценки по умолчанию, но ученики SVM не делают (см. predict).

Чтобы задать пользовательскую функцию потерь, используйте обозначение указателя на функцию. Функция должна иметь эту форму:
```
lossvalue = lossfun(C,S,W,Cost)
```
- Выходной аргумент lossvalue скаляр.
- Вы задаете имя функции (lossfun).
- C n- K логическая матрица со строками, указывающими на класс, которому принадлежит соответствующее наблюдение. n количество наблюдений в Tbl или X, и K количество отличных классов (numel(Mdl.ClassNames). Порядок следования столбцов соответствует порядку класса в Mdl.ClassNames. Создайте C установкой C(p,q) = 1, если наблюдение p находится в классе q, для каждой строки. Установите все другие элементы строки p к 0.
- S n- K числовая матрица классификационных оценок. Порядок следования столбцов соответствует порядку класса в Mdl.ClassNamesS матрица классификационных оценок, похожих на выход predict.
- W n- 1 числовой вектор из весов наблюдения.
- Cost K- K числовая матрица затрат misclassification. Например, Cost = ones(K) – eye(K) задает стоимость 0 для правильной классификации и 1 для misclassification.

Пример: 'LossFun', @lossfun

Типы данных: char | string | function_handle

`'Weights'` — Веса наблюдения
`ones(size(X,1),1)` (значение по умолчанию) | числовой вектор | имя переменной в `Tbl`

Веса наблюдения в виде разделенной запятой пары, состоящей из 'Weights' и числовой вектор или имя переменной в Tbl.

Если Weights числовой вектор, затем размер Weights должно быть равно количеству строк в X или Tbl.
Если Weights имя переменной в Tbl, необходимо задать Weights как вектор символов или строковый скаляр. Например, если веса хранятся как Tbl.W, затем задайте Weights как 'W'. В противном случае программное обеспечение обрабатывает все столбцы Tbl, включая Tbl.W, как предикторы.

Если вы предоставляете веса, loss вычисляет взвешенную потерю классификации и нормирует веса, чтобы суммировать до значения априорной вероятности в соответствующем классе.

Типы данных: double | single | char | string

Выходные аргументы

свернуть все

`L` — Потеря классификации
числовой скаляр

Потеря классификации, возвращенная в виде числа. Интерпретация L зависит от Weights и LossFun.

Больше о

свернуть все

Потеря классификации

Функции Classification loss измеряют прогнозирующую погрешность моделей классификации. Когда вы сравниваете тот же тип потери среди многих моделей, более низкая потеря указывает на лучшую прогнозную модель.

Предположим следующее:

L является средневзвешенной потерей классификации.
n является объемом выборки.
_yj является наблюдаемой меткой класса. Программные коды это как –1 или 1, указывая на отрицательный или положительный класс (или первый или второй класс в ClassNames свойство), соответственно.
f (_Xj) является классификационной оценкой положительного класса для наблюдения (строка) j данных о предикторе X.
_mj = _yj f (_Xj) является классификационной оценкой для классификации наблюдения j в класс, соответствующий _yj. Положительные значения _mj указывают на правильную классификацию и не способствуют очень средней потере. Отрицательные величины _mj указывают на неправильную классификацию и значительно способствуют средней потере.
Весом для наблюдения j является _wj. Программное обеспечение нормирует веса наблюдения так, чтобы они суммировали к соответствующей предшествующей вероятности класса. Программное обеспечение также нормирует априорные вероятности так, чтобы они суммировали к 1. Поэтому

$\sum_{j = 1}^{n} w_{j} = 1.$

Эта таблица описывает поддерживаемые функции потерь, которые можно задать при помощи 'LossFun' аргумент значения имени.

Функция потерь	Значение `LossFun`	Уравнение
Биномиальное отклонение	`'binodeviance'`	$L = \sum_{j = 1}^{n} w_{j} \log {1 + \exp [- 2 m_{j}]} .$
Экспоненциальная потеря	`'exponential'`	$L = \sum_{j = 1}^{n} w_{j} \exp (- m_{j}) .$
Неправильно классифицированный уровень в десятичном числе	`'classiferror'`	$L = \sum_{j = 1}^{n} w_{j} I {{\hat{y}}_{j} \neq y_{j}} .$ ${\hat{y}}_{j}$ метка класса, соответствующая классу с максимальным счетом. I {·} является функцией индикатора.
Потеря стержня	`'hinge'`	$L = \sum_{j = 1}^{n} w_{j} \max {0, 1 - m_{j}} .$
Потеря логита	`'logit'`	$L = \sum_{j = 1}^{n} w_{j} \log (1 + \exp (- m_{j})) .$
Минимальный ожидал стоимость misclassification	`'mincost'`	`'mincost'` является соответствующим, только если классификационные оценки являются апостериорными вероятностями. Программное обеспечение вычисляет взвешенную минимальную ожидаемую стоимость классификации с помощью этой процедуры для наблюдений j = 1..., n. Оцените ожидаемую misclassification стоимость классификации наблюдения _Xj в класс k: $γ_{j k} = {(f {(X_{j})}^{'} C)}_{k} .$ f (_Xj) является вектор-столбцом апостериорных вероятностей класса для двоичного файла и классификации мультиклассов для наблюдения _Xj. C является матрицей стоимости, сохраненной в `Cost` свойство модели. Для наблюдения j предскажите, что метка класса, соответствующая минимальному, ожидала стоимость misclassification: ${\hat{y}}_{j} = \underset{k = 1, ..., K}{argmin} γ_{j k} .$ Используя C, идентифицируйте, что стоимость подверглась (_cj) для того, чтобы сделать предсказание. Взвешенное среднее минимального ожидало, что потеря стоимости misclassification $L = \sum_{j = 1}^{n} w_{j} c_{j} .$ Если вы используете матрицу стоимости по умолчанию (чье значение элемента 0 для правильной классификации и 1 для неправильной классификации), то `'mincost'` потеря эквивалентна `'classiferror'` потеря.
Квадратичная потеря	`'quadratic'`	$L = \sum_{j = 1}^{n} w_{j} {(1 - m_{j})}^{2} .$

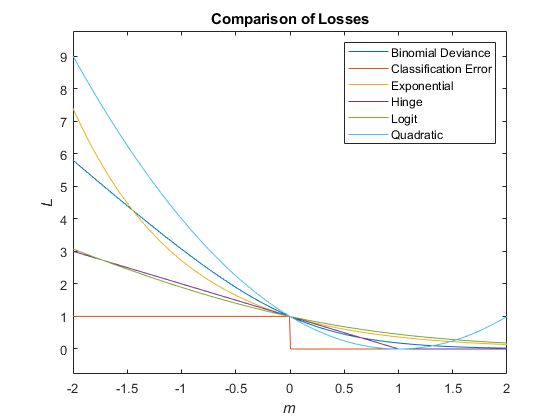
Этот рисунок сравнивает функции потерь (кроме 'mincost') по счету m для одного наблюдения. Некоторые функции нормированы, чтобы пройти через точку (0,1).

Расширенные возможности

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Указания и ограничения по применению:

loss не поддерживает высокий table данные.

Для получения дополнительной информации см. Раздел "Высокие массивы".

Введенный в R2017b

Документация

loss

Синтаксис

Описание

Примеры

Оцените потерю классификации наборов тестов

Задайте пользовательскую потерю классификации

Входные параметры

`Mdl` — Бинарная модель классификации ядер
`ClassificationKernel` объект модели

`X` — Данные о предикторе
n-by-p числовая матрица

`Y` — Метки класса
категориальный массив | символьный массив | массив строк | логический вектор | числовой вектор | массив ячеек из символьных векторов

`Tbl` — Выборочные данные
таблица

`ResponseVarName` — Имя переменной отклика
имя переменной в `Tbl`

Аргументы в виде пар имя-значение

`'LossFun'` — Функция потерь
`'classiferror'` (значение по умолчанию) | `'binodeviance'` | `'exponential'` | `'hinge'` | `'logit'` | `'mincost'` | `'quadratic'` | указатель на функцию

`'Weights'` — Веса наблюдения
`ones(size(X,1),1)` (значение по умолчанию) | числовой вектор | имя переменной в `Tbl`

Выходные аргументы

`L` — Потеря классификации
числовой скаляр

Больше о

Потеря классификации

Расширенные возможности

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Смотрите также

Документация Statistics and Machine Learning Toolbox

Поддержка

Документация

loss

Синтаксис

Описание

Примеры

Оцените потерю классификации наборов тестов

Задайте пользовательскую потерю классификации

Входные параметры

Mdl — Бинарная модель классификации ядер ClassificationKernel объект модели

X — Данные о предикторе n-by-p числовая матрица

Y — Метки класса категориальный массив | символьный массив | массив строк | логический вектор | числовой вектор | массив ячеек из символьных векторов

Tbl — Выборочные данные таблица

ResponseVarName — Имя переменной отклика имя переменной в Tbl

Аргументы в виде пар имя-значение

'LossFun' — Функция потерь 'classiferror' (значение по умолчанию) | 'binodeviance' | 'exponential' | 'hinge' | 'logit' | 'mincost' | 'quadratic' | указатель на функцию

'Weights' — Веса наблюдения ones(size(X,1),1) (значение по умолчанию) | числовой вектор | имя переменной в Tbl

Выходные аргументы

L — Потеря классификации числовой скаляр

Больше о

Потеря классификации

Расширенные возможности

"Высокие" массивы Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Смотрите также

Документация Statistics and Machine Learning Toolbox

Поддержка

`Mdl` — Бинарная модель классификации ядер
`ClassificationKernel` объект модели

`X` — Данные о предикторе
n-by-p числовая матрица

`Y` — Метки класса
категориальный массив | символьный массив | массив строк | логический вектор | числовой вектор | массив ячеек из символьных векторов

`Tbl` — Выборочные данные
таблица

`ResponseVarName` — Имя переменной отклика
имя переменной в `Tbl`

`'LossFun'` — Функция потерь
`'classiferror'` (значение по умолчанию) | `'binodeviance'` | `'exponential'` | `'hinge'` | `'logit'` | `'mincost'` | `'quadratic'` | указатель на функцию

`'Weights'` — Веса наблюдения
`ones(size(X,1),1)` (значение по умолчанию) | числовой вектор | имя переменной в `Tbl`

`L` — Потеря классификации
числовой скаляр

"Высокие" массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.