Продольный анализ

В этом примере показано, как выполнить продольный анализ с помощью mvregress.

Загрузка демонстрационных данных.
Отображение данных на графике.
Задайте матрицы проекта.
Подбирайте модель.
Постройте подобранную модель.
Задайте упрощенную модель.
Соответствуйте упрощенной модели.
Проведите тест отношения правдоподобия.

Загрузка демонстрационных данных.

Загрузите демонстрационные продольные данные.

load longitudinalData

Матричный Y содержит данные об ответе для 16 индивидуумов. Ответ является уровнем в крови препарата, измеренного в пяти моментах времени (t = 0, 2, 4, 6, и 8). Каждая строка Y соответствует индивидууму, и каждый столбец соответствует моменту времени. Первыми восемью предметами является розетка, и вторыми восемью предметами является штекер. Это - симулированные данные.

Отображение данных на графике.

Отобразите данные на графике для всех 16 предметов.

figure()
t = [0,2,4,6,8];
plot(t,Y)
hold on

hf = plot(t,Y(1:8,:),'^');
hm = plot(t,Y(9:16,:),'o');
legend([hf(1),hm(1)],'Female','Male','Location','NorthEast')

title('Longitudinal Response')
ylabel('Blood Drug Level')
xlabel('Time')
hold off

Задайте матрицы проекта.

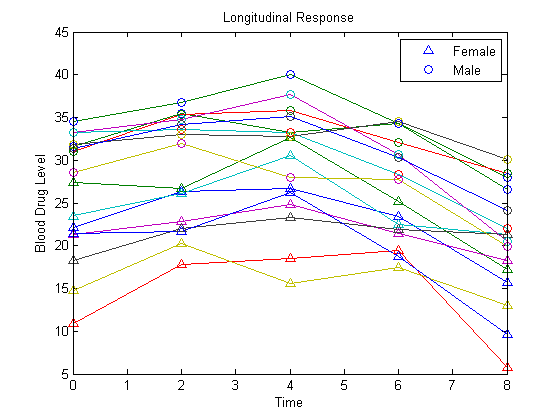
Позвольте _yij обозначить ответ для отдельного i = 1..., n, измеренный во времена _tij, j = 1..., d. В этом примере, n = 16 и d = 5. Позвольте _Gi обозначить пол отдельного i, где _Gi = 1 для штекеров и 0 для розеток.

Рассмотрите подбирать квадратичную продольную модель с отдельным наклоном и точкой пересечения для каждого пола,

$y_{i j} = β_{0} + β_{1} G_{i} + β_{2} t_{i j} + β_{3} t_{i j}^{2} + β_{4} G_{i} \times t_{i j} + β_{5} G_{i} \times t_{i j}^{2} + ε_{i j},$

где $ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ)$ . Ошибочные счета корреляции на кластеризацию в индивидууме.

Подбирать эту модель с помощью mvregress, данные об ответе должны быть в n-by-d матрицей. Y уже находится в соответствующем формате.

Затем создайте массив ячеек длины-n d-by-K матрицы проекта. Для этой модели существует K = 6 параметров.

Для отдельного i 5 6 матрица проекта

$X {i} = (\begin{matrix} 1 & G_{i} & t_{i 1} & t_{i 1}^{2} & G_{i} \times t_{i 1} & G_{i} \times t_{i 1}^{2} \\ 1 & G_{i} & t_{i 2} & t_{i 2}^{2} & G_{i} \times t_{i 2} & G_{i} \times t_{i 2}^{2} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & G_{i} & t_{i 5} & t_{i 5}^{2} & G_{i} \times t_{i 5} & G_{i} \times t_{i 5}^{2} \end{matrix}),$

соответствие вектору параметра

$β = (\begin{array}{l} β_{0} \\ β_{1} \\ ⋮ \\ β_{5} \end{array}) .$

Матричный X1 имеет матрицу проекта для розетки и X2 имеет матрицу проекта для штекера.

Создайте массив ячеек матриц проекта. Первые восемь индивидуумов являются розетками, и вторые восемь являются штекерами.

X = cell(8,1);
X(1:8) = {X1};
X(9:16) = {X2};

Подбирайте модель.

Подбирайте модель с помощью оценки наибольшего правдоподобия. Отобразите предполагаемые коэффициенты и стандартные погрешности.

[b,sig,E,V,loglikF] = mvregress(X,Y);
[b sqrt(diag(V))]

ans =

   18.8619    0.7432
   13.0942    1.0511
    2.5968    0.2845
   -0.3771    0.0398
   -0.5929    0.4023
    0.0290    0.0563

Коэффициенты на периодах взаимодействия (в последних двух строках b) не кажитесь значительными. Можно использовать значение целевой функции логарифмической правдоподобности для этой подгонки, loglikF, сравнить эту модель с одной без периодов взаимодействия с помощью теста отношения правдоподобия.

Постройте подобранную модель.

Постройте подходящие графики для розеток и штекеров.

Yhatf = X1*b;
Yhatm = X2*b;

figure()
plot(t,Y)
hold on

plot(t,Y(1:8,:),'^',t,Y(9:16,:),'o')

hf = plot(t,Yhatf,'k--','LineWidth',3);
hm = plot(t,Yhatm,'k','LineWidth',3);
legend([hf,hm],'Females','Males','Location','NorthEast')

title('Longitudinal Response')
ylabel('Blood Drug Level')
xlabel('Time')
hold off

Задайте упрощенную модель.

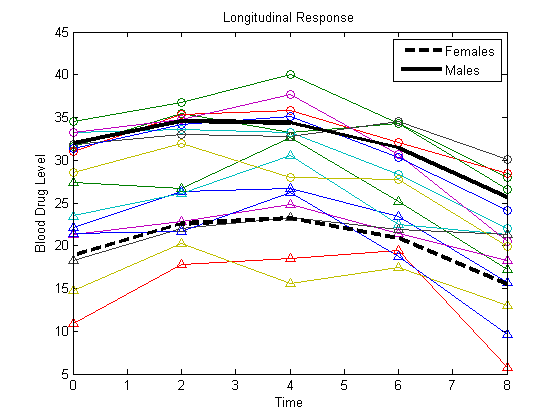
Подбирайте модель без периодов взаимодействия,

$y_{i j} = β_{0} + β_{1} G_{i} + β_{2} t_{i j} + β_{3} t_{i j}^{2} + ε_{i j},$

где $ε_{i} = (ε_{i 1}, \dots, ε_{i d})^{'} \sim M V N (0, Σ)$ .

Эта модель имеет четыре коэффициента, которые соответствуют первым четырем столбцам матриц проекта X1 и X2 (для розеток и штекеров, соответственно).

X1R = X1(:,1:4);
X2R = X2(:,1:4);

XR = cell(8,1);
XR(1:8) = {X1R};
XR(9:16) = {X2R};

Соответствуйте упрощенной модели.

Подбирайте эту модель с помощью оценки наибольшего правдоподобия. Отобразите предполагаемые коэффициенты и их стандартные погрешности.

[bR,sigR,ER,VR,loglikR] = mvregress(XR,Y);
[bR,sqrt(diag(VR))]

ans =

   19.3765    0.6898
   12.0936    0.8591
    2.2919    0.2139
   -0.3623    0.0283

Проведите тест отношения правдоподобия.

Сравните эти две модели с помощью теста отношения правдоподобия. Нулевая гипотеза - то, что упрощенная модель достаточна. Альтернатива - то, что упрощенная модель является несоответствующей (по сравнению с полной моделью с периодами взаимодействия).

Тестовая статистическая величина отношения правдоподобия сравнивается с распределением в квадрате хи с двумя степенями свободы (для этих двух пропускаемых коэффициентов).

LR = 2*(loglikF-loglikR);
pval = 1 - chi2cdf(LR,2)

pval =

    0.0803

p - значение 0.0803 указывает, что нулевая гипотеза не отклоняется на 5%-м уровне значения. Поэтому существуют недостаточные доказательства, что дополнительные условия улучшают подгонку.

Смотрите также

mvregress | mvregresslike

Документация