Оштрафованный порог для вейвлета 1D или 2D шумоподавление
THR = wbmpen(C,L,SIGMA,ALPHA)
wbmpen(C,L,SIGMA,ALPHA,ARG)
THR = wbmpen(C,L,SIGMA,ALPHA) возвращает глобальный порог THR для шумоподавления. THR получен содействующим правилом выбора вейвлета с помощью метода пенализации, предоставленного Birgé-Massart.
[C,L] структура разложения вейвлета сигнала или изображения, чтобы быть denoised.
SIGMA стандартное отклонение нулевого среднего Гауссова белого шума в модели шумоподавления (см. wnoisest для получения дополнительной информации.
ALPHA настраивающийся параметр для термина штрафа. Это должно быть вещественное число, больше, чем 1. Разреженность представления вейвлета сигнала denoised или изображения растет с ALPHA. Обычно ALPHA = 2.
THR минимизирует оштрафованный критерий, данный следующим:
Позвольте t* быть минимизатором
crit(t) = -sum(c(k)^2,k≤t) + 2*SIGMA^2*t*(ALPHA + log(n/t))
где c(k) коэффициенты вейвлета, отсортированные в порядке убывания их абсолютного значения и n количество коэффициентов; затем THR = | c (t*) |.
wbmpen(C,L,SIGMA,ALPHA,ARG) вычисляет глобальный порог и, кроме того, строит три кривые:
2*SIGMA^2*t*(ALPHA + log(n/t))
sum(c(k)^2,k²t)
crit(t)
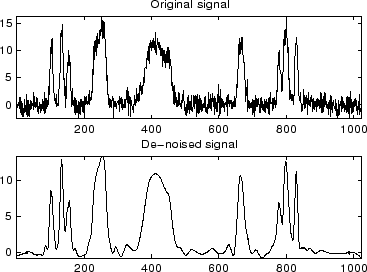
% Example 1: Signal denoising.
% Load noisy bumps signal.
load noisbump; x = noisbump;
% Perform a wavelet decomposition of the signal
% at level 5 using sym6.
wname = 'sym6'; lev = 5;
[c,l] = wavedec(x,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1, using wnoisest.
sigma = wnoisest(c,l,1);
% Use wbmpen for selecting global threshold
% for signal denoising, using the tuning parameter.
alpha = 2;
thr = wbmpen(c,l,sigma,alpha)
thr =
2.7681
% Use wdencmp for denoising the signal using the above
% threshold with soft thresholding and approximation kept.
keepapp = 1;
xd = wdencmp('gbl',c,l,wname,lev,thr,'s',keepapp);
% Plot original and denoised signals.
figure(1)
subplot(211), plot(x), title('Original signal')
subplot(212), plot(xd), title('De-noised signal')
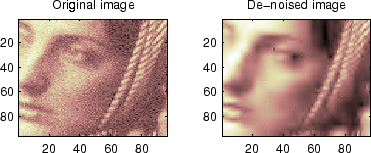
% Example 2: Image denoising.
% Load original image.
load noiswom;
nbc = size(map,1);
% Perform a wavelet decomposition of the image
% at level 3 using coif2.
wname = 'coif2'; lev = 3;
[c,s] = wavedec2(X,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1.
det1 = detcoef2('compact',c,s,1);
sigma = median(abs(det1))/0.6745;
% Use wbmpen for selecting global threshold
% for image denoising.
alpha = 1.2;
thr = wbmpen(c,l,sigma,alpha)
thr =
36.0621
% Use wdencmp for denoising the image using the above
% thresholds with soft thresholding and approximation kept.
keepapp = 1;
xd = wdencmp('gbl',c,s,wname,lev,thr,'s',keepapp);
% Plot original and denoised images.
figure(2)
colormap(pink(nbc));
subplot(221), image(wcodemat(X,nbc))
title('Original image')
subplot(222), image(wcodemat(xd,nbc))
title('De-noised image')