Aerospace Toolbox позволяет моделировать и визуализировать спутники на орбите, вычислять доступ к наземным станциям, визуализировать и анализировать линии связи с помощью satelliteScenario объект. В этом разделе представлен обзор технических терминов, часто встречающихся при визуализации сценариев.
Геодезическая система использует координаты (lat, lon, h) для представления положения относительно опорного эллипсоида. Все геодезические координаты в сценарии спутника используют WGS84 эллипсоид в качестве опорного эллипсоида. Координатное начало WGS 84 должно располагаться в центре масс Земли.
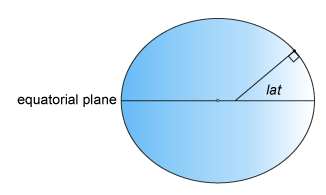
лат, широта, берёт начало на экваторе. Более конкретно, широта точки - это угол, нормаль к эллипсоиду в этой точке составляет с экваториальной плоскостью, которая содержит центр и экватор эллипсоида. Угол широты находится в диапазоне [-90 °, 90 °]. Положительные широты соответствуют северным, а отрицательные - южным.
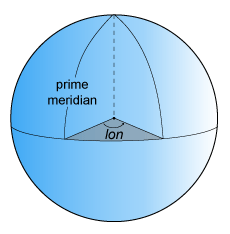
лон, долгота, берёт начало у простого меридиана. Более конкретно, долгота точки - это угол, который плоскость, содержащая центр эллипсоида и меридиан, содержащий эту точку, образует с плоскостью, содержащей центр эллипсоида и простой меридиан. Положительные долготы измеряются в направлении против часовой стрелки от точки обзора над Северным полюсом. Обычно долгота находится в диапазоне [-180 °, 180 °] или [0 °, 360 °].
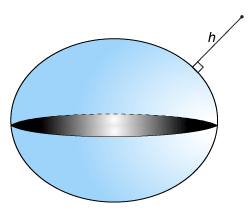
h, эллипсоидальная высота, измеряется вдоль нормали эталонного сфероида.
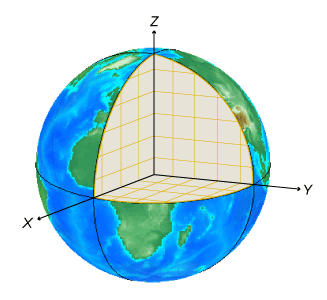
Система с земной привязкой (ECEF) использует декартовы координаты (X, Y, Z) для представления положения относительно центра опорного эллипсоида. Расстояние между центром эллипсоида и центром Земли зависит от опорного эллипсоида.
Положительная ось X пересекает поверхность эллипсоида при 0 ° широты и 0 ° долготы, где экватор встречается с простым меридианом.
Положительная ось Y пересекает поверхность эллипсоида при 0 ° широты и 90 ° долготы.
Положительная ось Z пересекает поверхность эллипсоида на 90 ° широты и 0 ° долготы, Северного полюса.
[1]
Чтобы описать точку в пространстве, нужна опорная рамка, которая не вращается относительно звёзд. Геоцентрический небесный опорный кадр (GCRF) с началом координат в центре Земли и ортогональными векторами I, J и K используется в качестве опорного кадра при добавлении satellite объекты в satelliteScenario. Фундаментальной плоскостью является плоскость I, J, которая тесно связана с экватором с небольшим смещением, а K тесно совпадает с северным полюсом. Расположение спутника можно описать с помощью вектора положения и вектора скорости в геоцентрико-экваториальной системе координат.
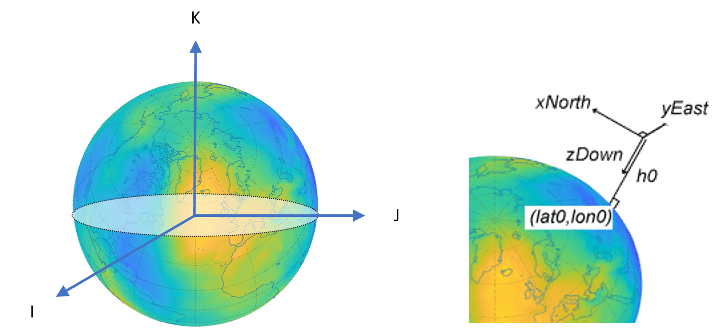
При обращении к положению спутников, скорости, ускорению, ориентации и угловой скорости всегда следует упомянуть систему координат, в которой они выражены. Глобальные системы, такие как GCRF и геодезические системы, описывают положение объекта с помощью триплета координат. Локальные системы, такие как NED и AER, требуют двух триплетов координат: один триплет описывает местоположение начала координат, а другой триплет описывает расположение объекта относительно начала координат.
Система «север-восток-вниз» (NED) использует декартовы координаты (xNorth, yEast, zDown) для представления положения относительно локального начала координат. Локальное начало координат описывается геодезическими координатами (lat0, lon0, h0). Обычно локальное начало системы NED находится над поверхностью Земли.
Положительная ось xNorth указывает на север вдоль меридиана долготы, содержащего lon0.
Положительная ось yEast указывает на восток вдоль параллели широты, содержащей лат0.
Положительная ось zDown указывает вниз вдоль эллипсоидной нормали.
Система координат NED обычно используется для задания местоположения относительно движущегося спутника. Следует отметить, что координаты не зафиксированы на кадре спутника.
Три линии проходят через спутник и пересекаются под прямым углом в центре масс спутника. Эти оси движутся вместе со спутником и вращаются относительно Земли вместе с кораблем.
Вращение вокруг оси «вперед-назад» называется креном.
Поворот вокруг оси «сторона к стороне» называется шагом.
Поворот вокруг вертикальной оси называется рысканием.

Углы рыскания, тангажа и крена спутников соответствуют стандарту ISO. Эти углы имеют положительные направления по часовой стрелке при взгляде в положительном направлении осей. Если не указано иное, по умолчанию в Aerospace Toolbox для этих углов используется порядок поворота «шаг-шаг-наклон».
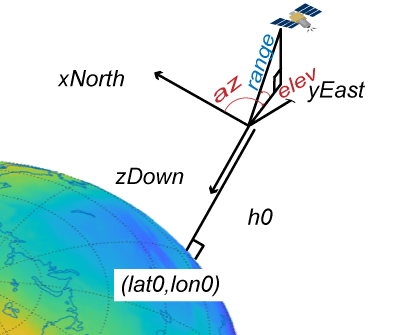
Система AER использует сферические координаты (az, elev, range) для представления положения относительно локального начала координат. Локальное начало координат описывается геодезическими координатами (lat0, lon0, h0). Азимут, отметка и диапазон наклона зависят от локальной декартовой системы, например системы NED .
az, азимут - угол по часовой стрелке в плоскости xEast-yNorth от положительной оси yNorth до проекции объекта в плоскость.
elev - это угол от плоскости xEast-yNorth до объекта.
диапазон, наклонный диапазон, - евклидово расстояние между объектом и локальным началом координат.
Орбитальные элементы - это параметры, необходимые для однозначной идентификации конкретной орбиты. Для однозначного определения орбиты и положения спутника на орбите требуется не менее шести параметров. Три параметра описывают, как выглядит орбитальная плоскость и положение спутника в эллипсе, а три других параметра описывают, как эта плоскость ориентирована в небесной инерциальной системе отсчета и где спутник находится в этой плоскости. Эти шесть параметров называются элементами Кеплера или орбитальными элементами.
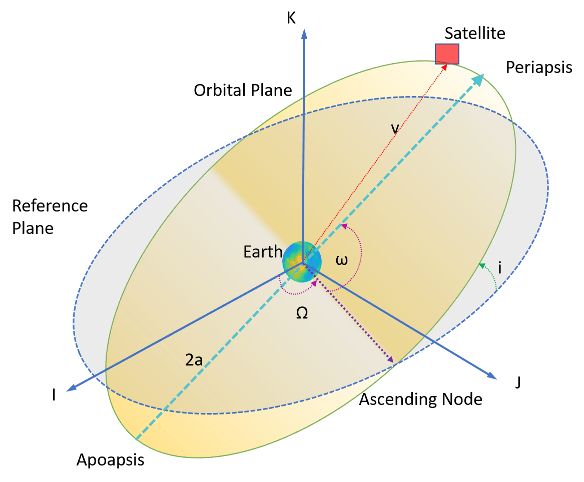
На этой диаграмме орбитальная плоскость (жёлтая) пересекает опорную плоскость (серая). Для спутников на околоземной орбите опорной плоскостью обычно является плоскость I-J геоцентрической небесной системы координат (GCRF).
Форму и размер эллипса определяют два элемента:
Эксцентриситет (e) - форма эллипса, описывающая, насколько он вытянут по сравнению с окружностью.
Большая полуось (a) - сумма расстояний периапсиса и апоапсиса, деленная на два. Периапсис - точка, в которой орбитальный объект находится ближе всего к центру массы тела, на котором он вращается. Апоапсис - точка, в которой орбитальный объект находится дальше всего от центра масс тела, на котором он вращается. Для классических орбит с двумя телами большая полуось - это расстояние между центрами тел.
Следующие два элемента определяют ориентацию орбитальной плоскости, в которую встроен эллипс:
Наклон (i) - вертикальный наклон эллипса относительно опорной плоскости, измеренный в восходящем узле (где орбита проходит вверх через опорную плоскость, зеленый угол i на диаграмме). Угол наклона измеряют перпендикулярно линии пересечения орбитальной плоскости и опорной плоскости. Любые три точки эллипса определяют орбитальную плоскость эллипса.
Начиная с экваториальной орбиты, орбитальная плоскость может быть наклонена вверх. Угол, наклоненный вверх от экватора, называется углом наклона, i. Поскольку центр Земли всегда должен находиться в орбитальной плоскости, точка на орбите, где спутник проходит экватор на пути вверх, называется восходящим узлом, и точка, где спутник проходит экватор на пути вниз, является нисходящим узлом. Линия, проходящая через эти две точки на экваторе, определяет линию узлов.
Правое вознесение восходящего узла (Λ) - горизонтальная ориентация восходящего узла эллипса (где орбита проходит вверх через опорную плоскость) относительно оси I опорной рамки.
Поворот правого подъема восходящего узла (RAAN) может быть любым числом между 0 и 360 °.
Остальные два элемента являются следующими:
Аргумент периапсиса (λ) - ориентация эллипса в орбитальной плоскости, как угол, измеряемый от восходящего узла до периапсиса.
Истинная аномалия (v) - положение орбитального тела вдоль эллипса в определенное время. Положение спутников на пути измеряется против часовой стрелки от периапсиса и называется истинной аномалией,
Aerospace Toolbox принимает файлы двухстрочных элементов (TLE) в качестве входных данных для satellite. Чтобы загрузить файлы TLE, посетите веб-сайт Space track.
Двухстрочный набор элементов - формат данных, кодирующий список орбитальных элементов околоземного орбитального объекта для данного момента времени, эпохи. Параметры орбитальных элементов могут быть закодированы как текст в ряде форматов. Наиболее распространённым из них является формат NASA/NORAD «двухстрочные элементы». Как обычно используется сегодня, каждый спутник получает три линии - одну линию, содержащую имя спутника, за которой следуют стандартные две линии элементов.
Данные для каждого спутника состоят из трех линий.
Satellite 1 1 25544U 98067A 04236.56031392 .00020137 00000-0 16538-3 0 9993 2 25544 51.6335 344.7760 0007976 126.2523 325.9359 15.70406856328906
Строка 1 - одиннадцатисимвольное имя спутника.
Строки 2 и 3 представляют собой стандартный формат набора двухстрочных элементов, идентичный формату, используемому NORAD и NASA.
| Колонка | Описание | Пример |
|---|---|---|
| 1 | Номер строки | 1 |
| 3 — 7 | Номер спутника | 25544 |
| 8 | Классификация Elset | U |
| 10 — 17 | Международный обозначитель | 98067A |
| 19 — 32 | Период набора элементов (UTC) | 04236.56031392 |
| 34 — 43 | Первая производная среднего движения по времени | .00020137 |
| 45 — 52 | Вторая производная среднего движения относительно времени (предполагается десятичная точка) | 00000-0 |
| 54 — 61 | Термин перетаскивания BSTAR. | 16538-3 |
| 63 | Тип набора элементов | 0 |
| 65 — 68 | Номер элемента | 999 |
| 69 | Контрольная сумма (по модулю 10) | 3 |
| Колонка | Описание | Примеры |
|---|---|---|
| 1 | Номер строки данных элемента | 2 |
| 3 — 7 | Номер спутника | 25544 |
| 9 — 16 | Наклон [градусы] | 51.6335 |
| 18 — 25 | Правое вознесение восходящего узла [градусы] | 344.7760 |
| 27 — 33 | Эксцентриситет (начальная десятичная точка) | 0007976 |
| 35 — 42 | Аргумент перигея [градусы] | 126.2523 |
| 44 — 51 | Средняя аномалия [градусы] | 325.9359 |
| 53 — 63 | Среднее движение [рев. в день] | 15.70406856 |
| 64 — 68 | Число оборотов в эпоху [Revs] | 32890 |
| 69 | Контрольная сумма (по модулю 10) | 6 |
В зависимости от приложения и орбиты объекта данные, полученные из TLE старше 30 дней, могут стать ненадежными. Орбитальные позиции могут рассчитываться по TLE через алгоритмы SGP4 и SDP4.
[1] «HSF - орбитальные элементы». Доступ состоялся 30 ноября 2020 года. https://spaceflight.nasa.gov/realdata/elements/graphs.html.
[2] "CelesTrak:" Часто задаваемые вопросы: формат набора двухстрочных элементов ", 26 марта 2016 г. https://web.archive.org/web/20160326061740/http ://celestrak.com/columns/v04n03/.
[1] Выравнивание границ и меток областей является представлением функции, предоставляемой поставщиками данных, и не подразумевает одобрения MathWorks ®.