Продольное колесо

Продольное колесо с диском, барабаном или реперным тормозом

Библиотека:
Блок силового агрегата/привод/колеса
Блоксеть/колеса и шины Vehicle Dynamics

Описание

Блок продольного колеса реализует продольное поведение идеального колеса. Можно указать метод расчета продольной силы и сопротивления качению, а также тип тормоза. Использовать блок при моделировании трансмиссии и продольного движения транспортного средства, где для определения ускорения, торможения и сопротивления качению колеса требуются низкочастотные силы движения шины и торможения. Например, можно использовать блок для определения требований к крутящему моменту и мощности для указанного цикла привода или события торможения. Блок не подходит для применений, требующих комбинированного бокового скольжения.

Существует четыре типа блоков продольных колес. Каждый блок реализует свой тип тормоза.

Имя блока	Настройка типа тормоза	Внедрение тормозов
Продольное колесо - без тормоза	`None`	Ничего
Продольное колесо - дисковый тормоз	`Disc`	Тормоз, преобразующий давление тормозного цилиндра в тормозное усилие.
Продольное колесо - барабанный тормоз	`Drum`	Симплексный барабанный тормоз, преобразующий приложенную силу и геометрию тормоза в чистый тормозной момент.
Продольное колесо - отображенный тормоз	`Mapped`	Таблица поиска, которая является функцией скорости колеса и приложенного тормозного давления.

Блок моделирует продольную силу как функцию проскальзывания колеса относительно поверхности дороги. Чтобы рассчитать продольную силу, задайте один из этих параметров.

Настройка	Блокирование реализации
`Magic Formula constant value`	Магическая формула с постоянным коэффициентом жесткости, формы, пика и кривизны.
`Magic Formula pure longitudinal slip`	Магическая формула с зависимыми от нагрузки коэффициентами, которые реализуют уравнения 4.E9- 4.E18 в динамике шин и транспортных средств.
`Mapped force`	Таблица поиска, которая является функцией нормального коэффициента силы и проскальзывания колеса.

Чтобы рассчитать крутящий момент сопротивления качению, задайте один из этих параметров сопротивления качению.

Настройка	Блокирование реализации
`None`	Ничего
`Pressure and velocity`	Метод в методологии ступенчатого выбега для измерения сопротивления качению шины. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых автомобилей, грузовых автомобилей и шин - Испытание в одной точке и корреляция результатов измерений.
`Magic Formula`	Уравнения магических формул из 4.E70 в Tire и Vehicle Dynamics. Магическая формула - эмпирическое уравнение, основанное на коэффициентах подгонки.
`Mapped torque`	Таблица поиска, которая является функцией продольной скорости нормальной силы и оси вращения.

Чтобы рассчитать вертикальное движение, задайте один из этих параметров.

Настройка	Блокирование реализации
`None`	Блок передает приложенные усилия шасси непосредственно на расчеты сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости и демпфирования колеса. Жесткость является функцией смещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Динамика вращательного колеса

Блок вычисляет инерционный отклик колеса в зависимости от:

Потери оси
Тормозной момент и крутящий момент привода
Сопротивление качению шины
Контакт с землей через интерфейс шины-дорога

Входной крутящий момент представляет собой сумму приложенного крутящего момента оси, тормозного момента и момента, возникающего из комбинированного крутящего момента шины.

$_{Ti} =_{} {Ta}_{} -_{}$ Tb + Td

На момент, возникающий от комбинированного крутящего момента шины, блок реализует тяговые силы колес и сопротивление качению с динамикой первого порядка. Сопротивление качению имеет постоянную времени, параметризованную в терминах длины релаксации.

$_{Td} (s) \frac{}{\frac{= 1_{|}}{_{}}}_{λ 'ReLes} +_{} 1_{(}$ Fx Re + My)

Для расчета крутящего момента сопротивления качению можно задать один из этих параметров сопротивления качению.

Настройка	Блокирование реализации
`None`	Блок задает сопротивление качению, `M_y`, до нуля.
`Pressure and velocity`	Блок использует метод, описанный в методе SAE Stepwise Coastdown Methody для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости. В частности, $_{My} =_{} Re {a_{+}_{b 'Vx}^{} \| +_{}^{}_{}^{cVx2}} {_{Fzβpiα}}$ tanh (4Vx)
`ISO 28580`	Блок использует метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых автомобилей, грузовых автомобилей и шин - Испытание в одной точке и корреляция результатов измерений. Метод учитывает нормальную нагрузку, паразитные потери и тепловые поправки от условий испытания. В частности, $_{My} =_{} \frac{{Re}_{} (_{}}{_{FzCr1} +_{Kt} (_{Tamb}} -_{} Tmeas) -$ Fpl) tanh (λ)
`Magic Formula`	Блок вычисляет сопротивление качению, `M_y`, используя уравнения магической формулы из 4.E70 в динамике шин и транспортных средств. Магическая формула - эмпирическое уравнение, основанное на коэффициентах подгонки.
`Mapped torque`	Для сопротивления качению, `M_y`блок использует таблицу поиска, которая является функцией от нормальной силы и продольной скорости оси вращения.

Если тормоза включены, блок определяет заблокированное или разблокированное состояние торможения на основе идеализированной модели трения сухого сцепления. Основываясь на состоянии блокировки, блок реализует эти модели трения и динамические модели.

Если	Условие блокировки	Модель трения	Динамическая модель
$\begin{array}{l} _{}_{}_{} ω\neq0orTS<\|Ti+Tf-ωb\| \end{array}$	Незапертый	$\begin{array}{l} _{Tf} =_{} \\ {Tkhere}_{,}_{Tk}_{=}_{} {FcRеффмкктанh}_{} [4 \\ _{(} -_{} {λ d}_{)]}_{Ts} \\ _{=} \frac{_{}^{}_{}^{} FcRеффмкsReff}{=_{2}^{} (_{}^{Ro3}} \end{array}$ − Ri3) 3 (Ro2 − Ri2)	$\overset{}{}_{}_{ω˙J=−ωb+Ti+To}$
$\begin{array}{l} _{}_{}_{} ω=0andTS\geq\|Ti+Tf-ωb\| \end{array}$	Запертый	$_{Tf} =_{}$ Ts	$ω=0$

Уравнения используют эти переменные.

ω	Угловая скорость колеса
a	Компонент силы, не зависящий от скорости
b	Компонент силы линейной скорости
c	Компонент силы квадратичной скорости
_Le	Длина релаксации шины
J	Момент инерции
_Мой	Крутящий момент сопротивления качению
_Ta	Приложенный крутящий момент на оси
_TB	Тормозной момент
_Td	Комбинированный крутящий момент шины
_Tf	Момент трения
_Ti	Чистый входной крутящий момент
_Tk	Кинетический момент трения
_Кому	Чистый выходной крутящий момент
_Ts	Статический фрикционный момент
_ФК	Приложенное усилие сцепления
_Fx	Продольное усилие, создаваемое дорожным покрытием шины из-за проскальзывания
_Reff	Эффективный радиус сцепления
_Ro	Внешний радиус кольцевого диска
_Ri	Внутренний радиус кольцевого диска
_Ре	Эффективный радиус шины при нагрузке и при заданном давлении
_Vx	Скорость продольной оси
_Fz	Нормальная сила транспортного средства
_Cr	Постоянное сопротивление качению
_Tamb	Температура окружающей среды
_Tmeas	Измеренная температура для постоянной сопротивления качению
_Fpl	Паразитная потеря силы
_Kt	Коэффициент термокоррекции
ɑ	Показатель давления в шинах
β	Показатель нормальной силы
_пи	Давление в шинах
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Тормоза

Диск

Если задан параметр «Тип тормоза» Discблок реализует дисковый тормоз. На этом рисунке показаны вид сбоку и спереди дискового тормоза.

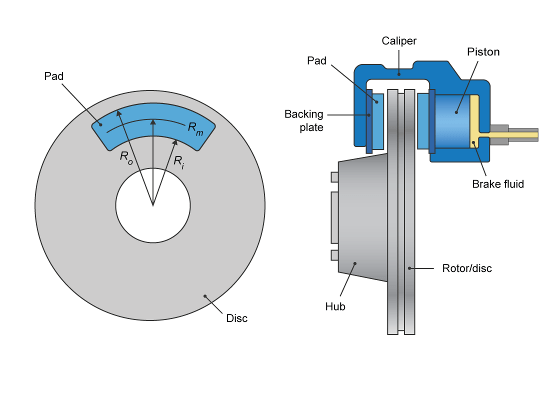
Front and side view of disc brake, showing pad, disc, and caliper

Дисковый тормоз преобразует давление в тормозном цилиндре в силу. Дисковый тормоз прикладывает усилие к среднему радиусу тормозной колодки.

Блок использует эти уравнения для вычисления тормозного момента дискового тормоза.

$T = \begin{matrix} \frac{{_{}^{}_{}_{}}{} мкPāBa2RmNpads4 при \\ \frac{_{N≠0μstaticPπBa2RmNpads4,}_{}^{когда}_{N}_{= 0}}{} \end{matrix}$

$Rm \frac{= Ro}{+}$ Ri2

Уравнения используют эти переменные.

T	Тормозной момент
P	Приложенное тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в узле дискового тормоза
_μstatic	Коэффициент статического трения дисковой площадки-ротора
μ	Коэффициент кинетического трения дисковой площадки-ротора
_Ba	Диаметр отверстия тормозного привода
_{Комната}	Средний радиус приложения усилия тормозной колодки к тормозному ротору
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если задан параметр «Тип тормоза» Drumблок реализует статический (стационарный) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двустороннего гидропривода и двух тормозных колодок. Тормозные колодки не имеют общего шарнирного пальца.

Симплексная модель барабанного тормоза использует приложенную силу и геометрию тормоза для расчета чистого крутящего момента для каждой тормозной колодки. Модель барабана предполагает, что приводы и геометрия колодки симметричны для обеих сторон, позволяя использовать единый набор параметров геометрии и трения для обеих колодок.

Блок реализует уравнения, полученные из этих уравнений в основах элементов машины.

$\begin{array}{l} _{Trshoe} = \frac{(½ мккр (_{} cosü 2 -_{}_{}^{}}{cosun1) Ba22μ (_{} 2r (_{} cosstart2 -^{}_{cosstart1}) +^{a}_{(} cos2ü 2 -_{}_{} cos2start1)) +_{} ar (_{2start1}} - \\ _{2ü 2 +} \frac{sin2start2 -_{} sin2start1))_{}_{}^{}}{PTlshoe = ({½ мккр}_{} (_{cosü 2} -^{cosun1})_{} {Ba2}^{−}_{} 2λ (2λ (2r (_{}_{}_{}_{}} \end{array}$

$T = \begin{matrix} _{{} {Trshoe}_{+} Tlshoe при N≠0 ( Trshoe + \\ _{Tlshoe)}_{} мкстатически, \frac{_{когда N}}{} = 0 \end{matrix}$

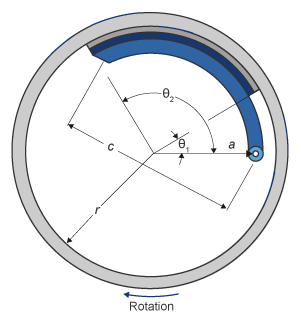
Side view of drum brake

Уравнения используют эти переменные.

T	Тормозной момент
P	Приложенное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент статического трения дисковой площадки-ротора
μ	Коэффициент кинетического трения дисковой площадки-ротора
_Trshoe	Тормозной момент правой колодки
_Tlshoe	Тормозной момент левой колодки
a	Расстояние от центра барабана до центра оси шарнира колодки
c	Расстояние от центра оси шарнира колодки до соединения тормозного привода на тормозной колодке
r	Внутренний радиус барабана
_Ba	Диаметр отверстия тормозного привода
_Θ1	Угол от центра оси шарнира колодки до начала материала тормозной колодки на колодке
_Θ2	Угол от центра оси шарнира колодки до конца материала тормозной колодки на колодке

Нанесенный на карту

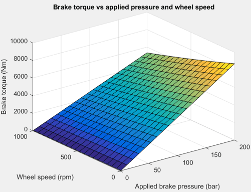
Если задан параметр «Тип тормоза» Mappedблок использует таблицу поиска для определения тормозного момента.

$T = \begin{matrix} _{{} fbrake (P, N ) при N≠0 ( мкстатически ) \\ \frac{_{fbrake (P,}}{} N)_{при} N = 0 \end{matrix}$

Уравнения используют эти переменные.

T	Тормозной момент
$_{fbreake}^{} (P,$ N)	Таблица поиска тормозного момента
P	Приложенное тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения поверхности поверхности контакта барабана в статических условиях
μ	Коэффициент трения поверхности раздела диск-подушка-ротор

Справочная таблица для тормозного момента, $_{fbreake}^{} (P,$ N), является функцией приложенного тормозного давления и скорости колеса, где:

T - тормозной момент в Н· м.
Р - давление торможения, в бар.
N - частота вращения колеса, в об/мин.

Plot of brake torque as a function of wheel speed and applied brake pressure

Продольная сила

Для моделирования продольных сил блока продольного колеса можно использовать магическую формулу. Модель обеспечивает установившуюся характеристическую функцию шины Fx = f (, Fz), продольную силу Fx на шине, _{основанную} на:

Вертикальная нагрузка Fz
Проскальзывание колесика

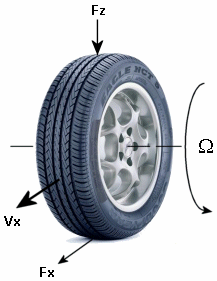
Image of tire with applied vertical and longitudinal forces

Эти переменные используются в модели Magic Formula.

Ω	Угловая скорость колеса
rw	Радиус колеса
Vx	Продольная скорость ступицы колеса
_rwΩ	Продольная скорость протектора шины
Vsx = rwΛ - Vx	Скорость скольжения колеса
t = Vsx/\| _Vx \|	Проскальзывание колеса
Фз, Fz0	Вертикальная нагрузка и номинальная вертикальная нагрузка на шину
Fx = f (в, _Fz)	Продольное усилие, прикладываемое к шине в точке контакта. Также характерная функция f шины.

Значение константы магической формулы

Если для параметра «Продольная сила» задано значение Magic Formula constant valueблок реализует магическую формулу как специфическую форму характеристической функции шины, характеризующуюся четырьмя безразмерными коэффициентами (B, C, D, E), или жесткостью, формой, пиком и кривизной:

$_{Fx} = f_{(,} {Fz}_{)} = {FzDsin}^{(} Ctan - 1 [{B^{}$

Наклон f при/= 0 равен BCD· _Fz.

Коэффициенты основаны на эмпирических данных шины. Эти значения являются типичными наборами постоянных коэффициентов магической формулы для общих дорожных условий.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Влажный тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Волшебная формула чистый продольный скольжение

Если для параметра «Продольная сила» задано значение Magic Formula pure longitudinal slipблок реализует более общую магическую формулу, используя безразмерные коэффициенты, которые являются функциями нагрузки шины. Блок реализует уравнения продольной силы, приведенные в главе 4 документа «Динамика шин и транспортных средств», включая 4.E9- 4.E18:

$\begin{array}{l} _{}_{} Fx0=Dxsin (_{}^{} Cxtan-1 [{_{}_{}_{} Bxκx-Ex_{}_{}^{}_{}_{} [Bxκx-tan-1 (Bxκx)]}])_{} \\ _{} +SVxwhere:κx =κ +_{} \\ _{} SHxCx =_{}_{} \\ _{}_{}_{}_{} \\ _{} pCx1λCxDx =μxFzς1μx = (_{} pDx1 +_{}_{} pDx2dfz)_{}_{}_{}_{}^{} (1+ppx3dpi+ppx4dpi2)_{}^{}^{}_{(1−pDx3γ2)} \\ _{} λ*μxEx_{= (}_{pEx1 +}_{} {pEx2dfz}_{+}_{}^{} pEx3dfz2)_{[}_{} 1-pEx4sgn_{} \\ {(κx)}_{]}_{} {λExKxκ}_{=} Fz_{(} {pKx1}_{+}_{pKx2dfz)}_{} exp_{} {(pKx3dfz)}_{} (1 +_{}_{}^{ppx1dpi} \\ +_{}_{} ppx2dpi2)_{}_{Основной обмен} =_{} \\ {Kxκ/}_{(} {CxDx}_{+} εx)_{} SHx_{=} \\ _{} pHx1 +_{}_{} {pHx2dfzSVx}_{=} {Fz}_{·} (_{}^{pVx1}_{+}_{} \end{array}$ pVx2dfz) λVxλ 'μxς1

_SHx и _SVx представляют смещения к скользящей и продольной силе в функции «сила-скольжение» или горизонтальные и вертикальные смещения, если функция отображается как кривая. _мкх - коэффициент трения, зависящий от продольной нагрузки. _αx - небольшое число, вставленное для предотвращения деления на ноль, когда _Fz приближается к нулю.

Вертикальная динамика

Если вертикальные степени свободы не выбраны, для параметра Вертикальное движение (Vertical Motion) задано значение Noneблок пропускает приложенные усилия шасси непосредственно к расчетам сопротивления качению и продольной силы.

Если для параметра «Вертикальное движение» задано значение Mapped stiffness and dampingвертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией смещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

$Fztire (\overset{}{}_{} z,z˙,Ptire)_{=} Fzk_{(z,}_{Ptire}) \overset{+}{}_{Fzb (}$ z˙,Ptire)

Блок определяет вертикальный отклик, используя это дифференциальное уравнение.

$\overset{}{} z m =_{} Fztire -$ Fz − мг

При отключении вертикальной степени свободы входная нормальная сила от транспортного средства переходит непосредственно к расчетам продольной силы и силы качения.

$\begin{array}{l} \overset{}{} \overset{}{} \\ z¨=z˙=m=0Fztire=mg \end{array}$

Блок использует закрепленную на колесе раму для разрешения вертикальных сил.

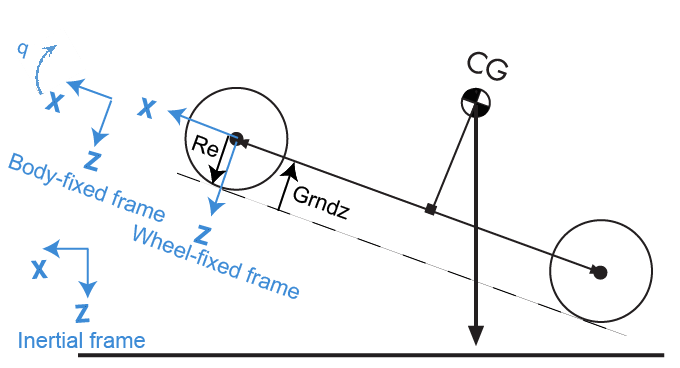
Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

Уравнения используют эти переменные.

Fztire	Нормальная сила шины вдоль оси Z, закрепленной на колесе
m	Масса оси
_Fzk	Нормальная сила шины, обусловленная жесткостью колеса вдоль оси Z, зафиксированной колесом
_Fzb	Нормальная сила шины из-за демпфирования колеса вдоль оси Z, закрепленной на колесе
_Fz	Подвеска или обычное усилие транспортного средства вдоль оси Z, закрепленной на колесе
_PTire	Давление в шинах
$\overset{}{} \overset{z,z˙,z¨}{}$	Смещение, скорость и ускорение шины соответственно вдоль оси Z, закрепленной на колесе

Учет мощности

Для учета мощности блок реализует эти уравнения.

Сигнал шины			Описание	Уравнения
`PwrInfo`	`PwrTrnsfrd` - Мощность, передаваемая между блоками Положительные сигналы указывают на поток в блок Отрицательные сигналы указывают на выход потока из блока	`PwrRoad`	Тяговая мощность, подаваемая от оси	$_{Proad} =_{}_{}$ FxVx
		`PwrAxlTrq`	Внешний крутящий момент, прилагаемый осью к колесу	$_{СТ} =$ Том
		`PwrFz`	Вертикальное усилие, приложенное к колесу транспортным средством или подвеской	$_{}_{} \overset{PFz=Fzz˙}{}$
	`PwrNotTrnsfrd` - Мощность, пересекающая границу блока, но не передаваемая Положительные сигналы указывают на вход Отрицательные сигналы указывают на потерю	`PwrSlip`	Тяговая потеря мощности	$_{P,} =_{}_{} FxVx +_{(} -_{}_{} FcRe$ + My)
		`PwrMyRoll`	Мощность сопротивления качению	$_{PMy} =_{}$ Myλ
		`PwrMyBrk`	Мощность торможения	$_{Pbrk} =_{}$ Mbrkλ
		`PwrMyb`	Потери на демпфирование при качении	$_{Pb} = -^{}$ bλ 2
		`PwrFzDamp`	Мощность вертикального демпфирования	$_{PFzb} =_{} \overset{}{}$ Fzbz˙
	`PwrStored` - Скорость изменения накопленной энергии Положительные сигналы указывают на увеличение Отрицательные сигналы указывают на снижение	`PwrStoredzdot`	Скорость изменения вертикальной кинетической энергии	$_{\overset{}{}} \overset{}{} \overset{Pz˙=mz¨z˙}{}$
		`PwrStoredq`	Скорость изменения кинетической энергии вращения	$_{}_{} \overset{}{} Pω=Iyyω˙ω$
		`PwrStoredFsFzSprng`	Скорость изменения запасенной потенциальной энергии боковой стенки	$_{}_{} {\overset{}{}}_{PFzk=Fzkz˙x}$
		`PwrStoredGrvty`	Скорость изменения гравитационной потенциальной энергии	$_{} \overset{Pg=-mgZ˙}{}$

Уравнения используют эти переменные.

ω	Угловая скорость колеса
b	Компонент силы линейной скорости
_Fx	Продольное усилие, создаваемое дорожным покрытием шины из-за проскальзывания
_Fcp	Усилие скольжения шины на контактном участке
_Fz	Нормальная сила транспортного средства
_Fzb	Нормальная сила шины из-за демпфирования колеса
_Fzk	Нормальная сила шины из-за жесткости колеса
_Iyy	Инерция вращения колеса
_Mbrk	Тормозной момент
_Мой	Крутящий момент сопротивления качению
_Ре	Эффективный радиус шины при нагрузке и при заданном давлении
T	Крутящий момент оси, приложенный к колесу
_Vx	Скорость продольной оси
$\overset{}{} \overset{z,z˙,z¨}{}$	Смещение, скорость и ускорение шины соответственно
ω	Угловая скорость колеса
$\overset{Z˙}{}$	Вертикальная скорость транспортного средства вдоль оси z, закрепленной на транспортном средстве

Порты

Вход

развернуть все

`BrkPrs` - Тормозное давление
`scalar`

Давление тормозов, в Па.

Зависимости

Чтобы включить этот порт, для параметра Brake Type укажите один из следующих типов:

Disc
Drum
Mapped

`AxlTrq` - Крутящий момент оси
`scalar`

Крутящий момент оси, _Та, вокруг оси вращения колеса, в Н· м.

`Vx` - Скорость
`scalar`

Продольная скорость оси вдоль оси X транспортного средства (кузова), в м/с.

`Fz` - Нормальная сила
`scalar`

Абсолютное значение нормальной силы подвески или транспортного средства вдоль оси z, зафиксированной на кузове, в Н.

`Gnd` - Смещение грунта
`scalar`

Смещение грунта, Grndz, вдоль отрицательной оси z, зафиксированной колесом, в м.

Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

Зависимости

Создать Gnd:

Задать вертикальное движение как Mapped stiffness and damping.
На панели «Вертикаль» выберите «Input ground displacement».

`lam_mux` - Коэффициент масштабирования трения
`scalar`

Масштабный коэффициент продольного трения, безразмерный.

Зависимости

Чтобы включить этот порт, выберите входной масштабный коэффициент трения.

`TirePrs` - Давление в шинах
`scalar`

Давление в шинах, в Па.

Зависимости

Чтобы включить этот порт:

Установите один из следующих параметров:
- Продольная сила к Magic Formula pure longitudinal slip.
- Сопротивление качению Pressure and velocity или Magic Formula.
- Вертикальное перемещение в Mapped stiffness and damping.
На панели «Динамика колес» выберите «Входное давление шины».

`Tamb` - Температура окружающей среды
`scalar`

Температура окружающей среды, _Tamb, в К.

Зависимости

Чтобы включить этот порт:

Установить сопротивление качению в ISO 28580.
На панели Сопротивление качению (Rolling Resistance) выберите для ввода температуру окружающей среды.

Продукция

развернуть все

`Info` - Сигнал шины
автобус

Сигнал шины, содержащий эти блочные вычисления.

Сигнал			Описание	Единицы
`AxlTrq`			Крутящий момент оси вокруг неподвижной оси Y корпуса	Н· м
`Omega`			Угловая скорость колеса вокруг неподвижной оси Y корпуса	рад/с
`Omegadot`			Угловое ускорение колеса относительно неподвижной оси Y корпуса	рад/с ^ 2
`Fx`			Продольное усилие транспортного средства вдоль оси Х, закрепленной на кузове	N
`Fz`			Вертикальная сила транспортного средства вдоль оси Z, закрепленной за кузовом	N
`Fzb`			Нормальная сила шины из-за демпфирования колеса вдоль оси Z, закрепленной на колесе	N
`Fzk`			Нормальная сила шины, обусловленная жесткостью колеса вдоль оси Z, зафиксированной колесом	N
`My`			Крутящий момент сопротивления качению вокруг неподвижной оси Y корпуса	Н· м
`Myb`			Крутящий момент сопротивления качению из-за демпфирования вокруг неподвижной оси Y корпуса	Н· м
`Kappa`			Коэффициент проскальзывания	НА
`Vx`			Продольная скорость транспортного средства вдоль оси Х, закрепленной на кузове	м/с
`Re`			Эффективный радиус колеса вдоль оси Z, закрепленной на колесе	m
`BrkTrq`			Тормозной момент вокруг неподвижной оси Y кузова	Н· м
`BrkPrs`			Давление тормоза	Pa
`z`			Вертикальное отклонение колеса вдоль оси Z, закрепленной на колесе	m
`zdot`			Вертикальная скорость колеса вдоль оси Z, зафиксированной колесом	м/с
`zddot`			Вертикальное ускорение колеса по оси Z	м/с ^ 2
`Gndz`			Смещение грунта по отрицательной оси Z-фиксированного колеса (положительный ввод обеспечивает подъем колеса)	m
`GndFz`			Вертикальное усилие колеса на земле по отрицательной оси Z, закрепленной за колесом	N
`TirePrs`			Давление в шинах	Pa
`Fpatch`			Тяговая мощность, подаваемая от оси
`PwrInfo`	`PwrTrnsfrd`	`PwrRoad`	Внешний крутящий момент, прилагаемый осью к колесу	W
		`PwrAxlTrq`	Вертикальное усилие, приложенное к колесу транспортным средством или подвеской	W
		`PwrFz`	Тяговая потеря мощности	W
	`PwrNotTrnsfrd`	`PwrSlip`	Мощность сопротивления качению	W
		`PwrMyRoll`	Мощность торможения	W
		`PwrMyBrk`	Потери на демпфирование при качении	W
		`PwrMyb`	Мощность вертикального демпфирования	W
		`PwrFzDamp`	Скорость изменения вертикальной кинетической энергии	W
	`PwrStored`	`PwrStoredzdot`	Скорость изменения кинетической энергии вращения	W
		`PwrStoredq`	Скорость изменения запасенной потенциальной энергии боковой стенки	W
		`PwrStoredFsFzSprng`	Скорость изменения гравитационной потенциальной энергии	W
		`PwrStoredGrvty`	Тяговая мощность, подаваемая от оси	W

`Fx` - Усилие продольной оси
`scalar`

Продольная сила, действующая на ось вдоль оси х, закрепленной на корпусе, в N. Положительная сила действует для перемещения транспортного средства вперед.

`Omega` - Угловая скорость колеса
`scalar`

Угловая скорость колеса, вокруг неподвижной оси Y корпуса, в рад/с.

`z` - Вертикальное отклонение колеса
`scalar`

Вертикальное отклонение колеса по оси Z, зафиксированной колесом, в м.

Зависимости

Чтобы включить этот порт, установите для параметра «Вертикальное движение» значение Mapped stiffness and damping.

`zdot` - Вертикальная скорость колеса
`scalar`

Вертикальная скорость колеса вдоль оси Z, в м/с.

Зависимости

Чтобы включить этот порт, установите для параметра «Вертикальное движение» значение Mapped stiffness and damping.

Параметры

развернуть все

Параметры блока

`Longitudinal Force` - Выберите тип
`Magic Formula constant value` (по умолчанию) | `Magic Formula pure longitudinal slip` | `Mapped force`

Настройка	Блокирование реализации
`Magic Formula constant value`	Магическая формула с постоянным коэффициентом жесткости, формы, пика и кривизны.
`Magic Formula pure longitudinal slip`	Магическая формула с зависимыми от нагрузки коэффициентами, которые реализуют уравнения 4.E9- 4.E18 в динамике шин и транспортных средств.
`Mapped force`	Таблица поиска, которая является функцией нормального коэффициента силы и проскальзывания колеса.

Зависимости

Выбор Включает эти параметры

Выбор	Включает эти параметры
`Magic Formula constant value`	Коэффициент чистого продольного пика, Dx Коэффициент чистой продольной формы, Cx Чистый коэффициент продольной жесткости, Bx Коэффициент чистой продольной кривизны, Ex
`Magic Formula pure longitudinal slip`	Коэффициент формы Cfx, PCX1 Продольное трение при номинальной нормальной нагрузке, PDX1 Изменение трения с нагрузкой, PDX2 Вариация трения с развалом, PDX3 Продольная кривизна при номинальной нормальной нагрузке, PEX1 Изменение коэффициента кривизны с нагрузкой, PEX2 Изменение коэффициента кривизны с квадратом нагрузки, PEX3 Коэффициент продольной кривизны с проскальзыванием, PEX4 Жесткость продольного скольжения при номинальной нормальной нагрузке, PKX1 Изменение жесткости скольжения с нагрузкой, PKX2 Коэффициент степени жесткости скольжения, PKX3 Горизонтальное смещение коэффициента проскальзывания при номинальной нормальной нагрузке, PHX1 Изменение коэффициента горизонтального проскальзывания с нагрузкой, PHX2 Вертикальное смещение нагрузки при номинальной нормальной нагрузке, PVX1 Изменение вертикального сдвига с нагрузкой, PVX2 Линейное изменение жесткости продольного скольжения при давлении в шине, PPX1 Квадратичное изменение жесткости продольного скольжения при давлении в шине, PPX2 Линейное изменение пикового продольного трения с давлением в шине, PPX3 Квадратичное изменение пикового продольного трения с давлением в шине, PPX4 Линейное изменение жесткости продольного скольжения при давлении в шине, PPX1 Коэффициент масштабирования функции спада скорости скольжения, lam_muV Коэффициент масштабирования жесткости при проскальзывании тормоза, lam_Kxkappa Коэффициент масштабирования продольной формы, lam_Cx Коэффициент масштабирования продольной кривизны, lam_Ex Коэффициент масштабирования продольного горизонтального сдвига, lam_Hx Коэффициент масштабирования продольного вертикального сдвига, lam_Vx
`Mapped force`	Контрольные точки коэффициента проскальзывания, kappaFx Нормальные силовые точки останова, FzFx Карта продольных сил, FxMap

Magic Formula constant value

Коэффициент чистого продольного пика, Dx

Коэффициент чистой продольной формы, Cx

Чистый коэффициент продольной жесткости, Bx

Коэффициент чистой продольной кривизны, Ex

Magic Formula pure longitudinal slip

Коэффициент формы Cfx, PCX1

Продольное трение при номинальной нормальной нагрузке, PDX1

Изменение трения с нагрузкой, PDX2

Вариация трения с развалом, PDX3

Продольная кривизна при номинальной нормальной нагрузке, PEX1

Изменение коэффициента кривизны с нагрузкой, PEX2

Изменение коэффициента кривизны с квадратом нагрузки, PEX3

Коэффициент продольной кривизны с проскальзыванием, PEX4

Жесткость продольного скольжения при номинальной нормальной нагрузке, PKX1

Изменение жесткости скольжения с нагрузкой, PKX2

Коэффициент степени жесткости скольжения, PKX3

Горизонтальное смещение коэффициента проскальзывания при номинальной нормальной нагрузке, PHX1

Изменение коэффициента горизонтального проскальзывания с нагрузкой, PHX2

Вертикальное смещение нагрузки при номинальной нормальной нагрузке, PVX1

Изменение вертикального сдвига с нагрузкой, PVX2

Линейное изменение жесткости продольного скольжения при давлении в шине, PPX1

Квадратичное изменение жесткости продольного скольжения при давлении в шине, PPX2

Линейное изменение пикового продольного трения с давлением в шине, PPX3

Квадратичное изменение пикового продольного трения с давлением в шине, PPX4

Линейное изменение жесткости продольного скольжения при давлении в шине, PPX1

Коэффициент масштабирования функции спада скорости скольжения, lam_muV

Коэффициент масштабирования жесткости при проскальзывании тормоза, lam_Kxkappa

Коэффициент масштабирования продольной формы, lam_Cx

Коэффициент масштабирования продольной кривизны, lam_Ex

Коэффициент масштабирования продольного горизонтального сдвига, lam_Hx

Коэффициент масштабирования продольного вертикального сдвига, lam_Vx

Mapped force

Контрольные точки коэффициента проскальзывания, kappaFx

Нормальные силовые точки останова, FzFx

Карта продольных сил, FxMap

`Rolling Resistance` - Выберите тип
`None` (по умолчанию) | `Pressure and velocity` | `ISO 28580` | `Magic Formula` | `Mapped torque`

Настройка	Блокирование реализации
`None`	Ничего
`Pressure and velocity`	Метод в методологии ступенчатого выбега для измерения сопротивления качению шины. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых автомобилей, грузовых автомобилей и шин - Испытание в одной точке и корреляция результатов измерений.
`Magic Formula`	Уравнения магических формул из 4.E70 в Tire и Vehicle Dynamics. Магическая формула - эмпирическое уравнение, основанное на коэффициентах подгонки.
`Mapped torque`	Таблица поиска, которая является функцией продольной скорости нормальной силы и оси вращения.

Зависимости

Выбор	Параметры
`Pressure and velocity`	Коэффициент силы, независимый от скорости, aMy Компонент силы линейной скорости, bMy Компонент силы квадратичной скорости, cMy Показатель давления в шинах, alphaMy Показатель нормальной силы, betaMy
`ISO 28580`	Сила паразитных потерь, Fpl Постоянная сопротивления качению, Cr Коэффициент термокоррекции, Кт Измеренная температура, Tmeas Сила паразитных потерь, Fpl Температура окружающей среды, Tamb
`Magic Formula`	Коэффициент крутящего момента сопротивления качению, QSY Коэффициент сопротивления качению продольной силой, QSY2 Коэффициент сопротивления качению с линейной скоростью вращения, QSY3 Коэффициент сопротивления качению при скорости вращения в квадрате, QSY4 Крутящий момент сопротивления качению в квадрате, QSY5 Крутящий момент сопротивления качению в квадрате развала на основе нагрузки, QSY6 Нормальный коэффициент сопротивления качению под нагрузкой, QSY7 Коэффициент сопротивления качению под давлением, QSY8 Коэффициент масштабирования сопротивления качению, lam_My
`Mapped torque`	Точки останова скорости по оси вращения, VxMy Нормальные силовые точки останова, FzMy Карта крутящего момента сопротивления качению, MyMap

`Brake Type` - Выберите тип
`None` | `Disc` | `Drum` | `Mapped`

Существует четыре типа блоков продольных колес. Каждый блок реализует свой тип тормоза.

Имя блока	Настройка типа тормоза	Внедрение тормозов
Продольное колесо - без тормоза	`None`	Ничего
Продольное колесо - дисковый тормоз	`Disc`	Тормоз, преобразующий давление тормозного цилиндра в тормозное усилие.
Продольное колесо - барабанный тормоз	`Drum`	Симплексный барабанный тормоз, преобразующий приложенную силу и геометрию тормоза в чистый тормозной момент.
Продольное колесо - отображенный тормоз	`Mapped`	Таблица поиска, которая является функцией скорости колеса и приложенного тормозного давления.

`Vertical Motion` - Выберите тип
`None` (по умолчанию) | `Mapped stiffness and damping`

Чтобы рассчитать вертикальное движение, задайте один из этих параметров.

Настройка	Блокирование реализации
`None`	Блок передает приложенные усилия шасси непосредственно на расчеты сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости и демпфирования колеса. Жесткость является функцией смещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Выбор Включает эти параметры Создает эти выходные порты

Выбор	Включает эти параметры	Создает эти выходные порты
`Mapped stiffness and damping`	Колесная и неподрессоренная масса, м Начальное отклонение, zo Начальная скорость, zdoto Гравитационное ускорение, g Точки останова вертикального отклонения, zFz Точки останова давления, pFz Сила из-за отклонения, Fzz Точки останова вертикальной скорости, zdotFz Сила из-за скорости, Fzzdot Смещение грунта, Gndz Смещение входного заземления	`z` `zdot`

Mapped stiffness and damping

Колесная и неподрессоренная масса, м

Начальное отклонение, zo

Начальная скорость, zdoto

Гравитационное ускорение, g

Точки останова вертикального отклонения, zFz

Точки останова давления, pFz

Сила из-за отклонения, Fzz

Точки останова вертикальной скорости, zdotFz

Сила из-за скорости, Fzzdot

Смещение грунта, Gndz

Смещение входного заземления

z

zdot

`Longitudinal scaling factor, lam_x` - Коэффициент масштабирования трения
`1` (по умолчанию)

Масштабный коэффициент продольного трения, безразмерный.

Зависимости

Чтобы включить этот параметр, снимите флажок Масштабный коэффициент трения на входе (Input friction scale factor).

`Input friction scale factor` - Выбор
`Off` (по умолчанию)

Создайте входной порт для масштабного коэффициента продольного трения.

Зависимости

Выбор этого параметра:

Создание входного порта lam_mux.
Отключает параметр Коэффициент продольного масштабирования, lam_x.

Динамика колес

`Axle viscous damping coefficient, br` - Демпфирование
`0.001` (по умолчанию) | `scalar`

Коэффициент демпфирования вязкости оси, br, в Н· м· с/рад.

`Wheel inertia, Iyy` - Инерция
`0.8` (по умолчанию) | `scalar`

Инерция колеса, в кг· м ^ 2.

`Wheel initial angular velocity, omegao` - Скорость колеса
`0` (по умолчанию) | `scalar`

Начальная угловая скорость колеса вдоль неподвижной по телу оси y в рад/с.

`Relaxation length, Lrel` - Длина релаксации
`0.5` (по умолчанию) | `scalar`

Длина релаксации колеса, в м.

`Loaded radius, Re` - Радиус нагрузки
`0.3` (по умолчанию) | `scalar`

Радиус нагруженного колеса, Re, в м.

Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

`Unloaded radius, UNLOADED_RADIUS` - Незагруженный радиус
`0.4` (по умолчанию) | `scalar`

Радиус незагруженного колеса, в м.

Зависимости

Чтобы создать этот параметр, задайте для параметра Сопротивление качению значение Pressure and velocity или Magic Formula.

`Nominal longitudinal speed, LONGVL` - Скорость
`16` (по умолчанию) | `scalar`

Номинальная продольная скорость вдоль закрепленной на корпусе оси х, в м/с.

Зависимости

Чтобы включить этот параметр, задайте для параметра Продольная сила значение Magic Formula pure longitudinal slip.

`Nominal camber angle, gamma` - Камбер
`0` (по умолчанию) | `scalar`

Номинальный угол развала, в рад.

Зависимости

Чтобы включить этот параметр, установите один из следующих параметров:

Продольная сила к Magic Formula pure longitudinal slip.
Сопротивление качению Magic Formula.

`Nominal pressure, NOMPRES` - Давление
`220000` (по умолчанию) | `scalar`

Номинальное давление, в Па

Зависимости

Чтобы включить этот параметр, установите один из следующих параметров:

Продольная сила к Magic Formula pure longitudinal slip.
Сопротивление качению Magic Formula.

`Pressure, press` - Давление
`220000` (по умолчанию) | `scalar`

Давление, в Па.

Зависимости

Чтобы включить этот параметр:

Установите одно из следующих значений:
- Продольная сила к Magic Formula pure longitudinal slip.
- Сопротивление качению Pressure and velocity или Magic Formula.
- Вертикальное перемещение в Mapped stiffness and damping.
На панели «Динамика колес» снимите флажок «Входное давление шины».

Продольный

Значение константы магической формулы

`Pure longitudinal peak factor, Dx` - Коэффициент
`1` (по умолчанию) | `scalar`

Чистый продольный пиковый коэффициент, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Влажный тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Для создания этого параметра выберите параметр «Продольная сила» Magic Formula constant value.

`Pure longitudinal shape factor, Cx` - Коэффициент
`1.65` (по умолчанию) | `scalar`

Чистый продольный коэффициент формы, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Влажный тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Для создания этого параметра выберите параметр «Продольная сила» Magic Formula constant value.

`Pure longitudinal stiffness factor, Bx` - Коэффициент
`10` (по умолчанию) | `scalar`

Чистый коэффициент продольной жесткости, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Влажный тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Для создания этого параметра выберите параметр «Продольная сила» Magic Formula constant value.

`Pure longitudinal curvature factor, Ex` - Коэффициент
`0.01` (по умолчанию) | `scalar`

Чистый коэффициент продольной кривизны, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Влажный тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Для создания этого параметра выберите параметр «Продольная сила» Magic Formula constant value.

Волшебная формула чистый продольный скольжение