Применение фазового шума к сигналу основной полосы частот
comm.PhaseNoise Система object™ добавляет фазовый шум к комплексному сигналу. Этот объект эмулирует нарушения, вносимые гетеродином передатчика или приемника беспроводной связи. Объект генерирует отфильтрованный фазовый шум в соответствии с заданной спектральной маской и добавляет его к входному сигналу. Описание моделирования фазового шума см. в разделе Алгоритмы.
Добавление фазового шума с помощью comm.PhaseNoise объект:
Создать comm.PhaseNoise и задайте его свойства.
Вызовите объект с аргументами, как если бы это была функция.
Дополнительные сведения о работе системных объектов см. в разделе Что такое системные объекты?.
phznoise = comm.PhaseNoise
phznoise = comm.PhaseNoise(Name,Value)Name установить в указанное значение Value. Можно указать дополнительные аргументы пары имя-значение в любом порядке как (Name1,Value1,...,NameN,ValueN).
phznoise = comm.PhaseNoise(level,offset,samplerate)
Чтобы использовать функцию объекта, укажите объект System в качестве первого входного аргумента. Например, для освобождения системных ресурсов объекта System с именем obj, используйте следующий синтаксис:
release(obj)
Добавьте вектор фазового шума и вектор сдвига частоты к 16-QAM сигналу. Затем постройте график сигнала.
Создайте объект системы фазового шума.
pnoise = comm.PhaseNoise('Level',-50,'FrequencyOffset',20);
Создание модулированных символов.
M = 16; % From 16-QAM
data = randi([0 M-1],1000,1);
modData = qammod(data,M);Использовать pnoise для приложения фазового шума. Постройте график поврежденных данных.
y = pnoise(modData); scatterplot(y)
Просмотрите влияние фазового шума на синусоидальную волну 10 МГц с помощью анализатора спектра. Настройте разрешающую способность анализатора спектра, чтобы увидеть его влияние на визуализированный спектральный шум.
Инициализация переменных для моделирования.
fc = 1e6; % Carrier frequency in Hz fs = 4e6; % Sample rate in Hz. phNzLevel = [-85 -118 -125 -145]; % Phase noise level in dBc/Hz phNzFreqOff = [1e3 9.5e3 19.5e3 195e3]; % Phase noise frequency offset in Hz Nspf = 6e6; % Number of Samples per frame freqSpan = 400e3; % Frequency span in Hz for spectrum computation
Создание объектов синусоидального, фазового шума и анализатора спектра.
sinewave = dsp.SineWave('Amplitude',1,'Frequency',fc,'SampleRate',fs, ... 'SamplesPerFrame',Nspf,'ComplexOutput',true); pnoise = comm.PhaseNoise('Level',phNzLevel, ... 'FrequencyOffset',phNzFreqOff,'SampleRate',fs); spectrumscopeRBW1 = dsp.SpectrumAnalyzer('NumInputPorts',2, ... 'SampleRate',fs,'FrequencySpan','Span and center frequency', ... 'CenterFrequency',fc,'Span',freqSpan,'RBWSource','Property', ... 'RBW',1,'SpectrumType','Power density','SpectralAverages',10, ... 'SpectrumUnits','dBW','YLimits',[-150 10], ... 'Title','Resolution Bandwidth 1 Hz','Position',[79 147 605 374]); spectrumscopeRBW10 = dsp.SpectrumAnalyzer('NumInputPorts',2, ... 'SampleRate',fs,'FrequencySpan','Span and center frequency', ... 'CenterFrequency',fc,'Span',freqSpan,'RBWSource','Property', ... 'RBW',10,'SpectrumType','Power density','SpectralAverages',10, ... 'SpectrumUnits','dBW','YLimits',[-150 10], ... 'Title','Resolution Bandwidth 10 Hz','Position',[685 146 605 376]);
Для анализа спектра и фазового шума пример включает два объекта анализатора спектра с полосами пропускания разрешения 1 Гц и 10 Гц соответственно. Объекты анализатора спектра используют значения по умолчанию Hann установка окна, единицы измерения установлены в dBW/Hzи число спектральных средних устанавливается равным 10.
x = sinewave(); y = pnoise(x);
Если разрешающая способность равна 1 Гц, dBW/Hz вид анализатора спектра показывает тональный сигнал при 0 дБт/Гц. Объект анализатора спектра корректирует эффект расширения мощности окна Ганна. Результаты показывают визуальное среднее фазового шума, соответствующего заданному спектру фазового шума.
spectrumscopeRBW1(x,y)
Если разрешающая способность равна 10 Гц, dBW/Hz вид анализатора спектра показывает тональный сигнал на частоте -10 дБт/Гц. Энергия тона синусоидальной волны теперь распределена по 10 Гц вместо 1 Гц, поэтому уровень синусоидальной PSD снижается на 10 дБ. При ширине полосы разрешения 10 Гц визуальное среднее фазового шума все еще достигает фазового шума, определенного объектом фазового шума.
При увеличении разрешающей способности с 1 Гц до 10 Гц объект анализатора спектра все еще корректирует эффект расширения мощности окна Ганна и обеспечивает лучшее спектральное усреднение с более широкой разрешающей способностью. Дополнительные сведения см. в разделе Зачем использовать Windows?.
spectrumscopeRBW10(x,y)
Вычислите среднеквадратичный фазовый шум в градусах между чистой и шумной синусоидальными волнами. В общем случае чистый сигнал должен быть выровнен по времени с шумным сигналом для точного определения фазовой ошибки. Однако в этом случае периодичность синусоидальной волны делает этот шаг ненужным.
ph_err = unwrap(angle(y) - angle(x));
rms_ph_nz_deg = rms(ph_err)*180/pi();
sprintf('The computed RMS phase noise is %3.2f degrees.\n',rms_ph_nz_deg)ans =
'The computed RMS phase noise is 0.18 degrees.
'
Выходной сигнал, yk, связан с входной последовательностью xk на yk = xkejoftk, где dwfk - фазовый шум. Фазовый шум фильтруется гауссовым шумом таким образом, что dwfk = f (nk), где nk - шумовая последовательность, и f представляет операцию фильтрации.
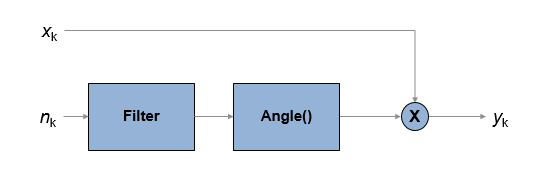
Для моделирования фазового шума определите характеристику маски плотности спектра мощности (PSD), задав скалярные или векторные значения для сдвига частоты и уровня фазового шума.
Для спецификации сдвига скалярной частоты и уровня фазового шума цифровой фильтр БИХ вычисляет спектральную маску. Спектральная маска имеет характеристику 1/f, которая проходит через указанную точку.
Для спецификации сдвига векторной частоты и уровня фазового шума фильтр КИХ вычисляет спектральную маску. Спектральная маска интерполируется через log10 (f). Он плоский от постоянного тока до самого низкого смещения частоты и от самого высокого смещения частоты до половины частоты дискретизации.
Цифровой фильтр БИХ
Для цифрового фильтра БИХ числительный коэффициент равен
,
где foffset - сдвиг частоты в Гц, а L - уровень фазового шума в дБк/Гц. Коэффициенты знаменателя γ i рекурсивно определяются как
1i − 1,
где γ 1 = 1, i = {1, 2,..., Nt} и Nt - число коэффициентов фильтра. Nt - степень 2, от 2от 7 до 219. Значение Nt растет, когда фазовый шум уменьшается до 0 Гц.
Фильтр FIR
Для КИХ-фильтра уровень фазового шума определяется посредством интерполяции log10 (f) для частотных смещений в диапазоне [df, fs/2], где df - частотное разрешение, а fs - частота дискретизации. Фазовый шум является плоским от 0 Гц до наименьшего сдвига частоты и от наибольшего сдвига частоты до fs/2. Разрешение частоты равно fs2 где Nt - число коэффициентов, и является степенью 2, меньшей или равной 216. Если Nt < 28, используется фильтр FIR временной области. В противном случае используется фильтр КИХ частотной области.
Алгоритм увеличивает Nt до тех пор, пока не будут выполнены следующие условия:
Разрешение частоты меньше минимального значения вектора сдвига частоты.
Разрешение частоты меньше минимальной разности между двумя последовательными частотами в векторе сдвига частоты.
Максимальное количество отводов фильтра FIR - 216.
[1] Kasdin, N.J., "Дискретное моделирование цветного шума и стохастических процессов и 1/( f _ α); Выработка шума по закону мощности. " Труды IEEE. том 83, № 5, май 1995, стр 802-827.