Квантование в секции квантования сигнала не требует априорного знания о переданном сигнале. На практике можно часто делать обоснованные догадки о настоящем сигнале на основе прошлых передач сигнала. Использование таких образованных догадок для содействия квантованию сигнала известно как предсказательное квантование. Наиболее распространенным способом предсказательного квантования является дифференциальная импульсная кодовая модуляция (DPCM).
Функции dpcmenco, dpcmdeco, и dpcmopt может помочь вам реализовать предсказательный квантователь DPCM с линейным предиктором.
Чтобы определить кодер для такого квантователя, вы должны предоставить не только раздел и кодовую книгу, как описано в «Представлять разделы и представлять кодовые книги», но также и предиктор. Предиктор - это функция, которую кодер DPCM использует для получения образованного предположения на каждом шаге. Линейный предиктор имеет вид
y(k) = p(1)x(k-1) + p(2)x(k-2) + ... + p(m-1)x(k-m+1) + p(m)x(k-m)
где x - исходный сигнал, y(k) попытки предсказать значение x(k), и p является m-кортеж вещественных чисел. Вместо квантования x сам кодер DPCM квантует предиктивную ошибку x-y. Целое число m выше называется прогнозирующим порядком. Особый случай, когда m = 1 называется дельта-модуляцией.
Если предположение для k-е значение сигнала x, на основе более ранних значений xявляется
y(k) = p(1)x(k-1) + p(2)x(k-2) +...+ p(m-1)x(k-m+1) + p(m)x(k-m)
тогда соответствующий вектор предиктора для функций панели инструментов
predictor = [0, p(1), p(2), p(3),..., p(m-1), p(m)]
Примечание
Начальный ноль в предикторном векторе имеет смысл, если рассматривать вектор как полиномиальную передаточную функцию фильтра конечной импульсной характеристики (FIR).
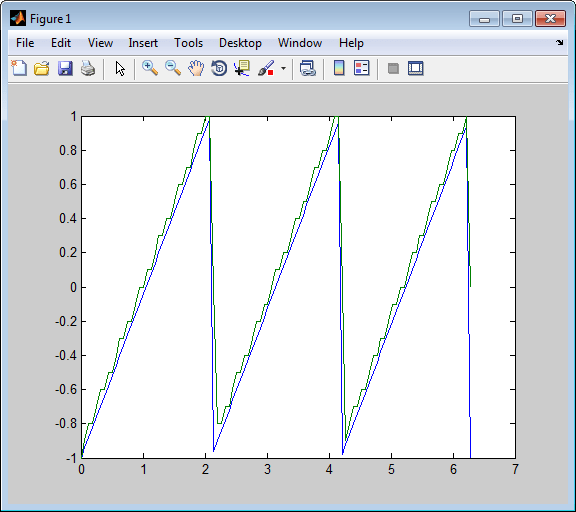
Простой частный случай DPCM квантует разность между текущим значением сигнала и его значением на предыдущем этапе. Таким образом, предсказатель просто y(k) = x (k - 1). Приведенный ниже код реализует эту схему. Он кодирует пилообразный сигнал, декодирует его и строит графики как исходного, так и декодированного сигнала. Сплошная линия является исходным сигналом, в то время как пунктирная линия является восстановленными сигналами. В примере также вычисляется среднеквадратическая ошибка между исходным и декодированным сигналами.
predictor = [0 1]; % y(k)=x(k-1) partition = [-1:.1:.9]; codebook = [-1:.1:1]; t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); plot(t,x,t,decodedx,'--') legend('Original signal','Decoded signal','Location','NorthOutside'); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выходные данные:
distor =
0.0327
В разделе «Оптимизация параметров квантования» описывается использование обучающих данных с lloyds функция, чтобы помочь найти параметры квантования, которые минимизируют искажение сигнала.
В этом разделе описаны аналогичные процедуры для использования dpcmopt функция в сочетании с двумя функциями dpcmenco и dpcmdeco, которые впервые появляются в предыдущем разделе.
Примечание
Данные обучения, используемые с dpcmopt должно быть типичным для типов сигналов, с которыми вы будете квантовать dpcmenco.
Этот пример аналогичен примеру, приведенному в последнем разделе. Однако, где был создан последний пример predictor, partition, и codebook в этом примере используется та же кодовая книга (которая теперь называется initcodebook) в качестве начального предположения для нового оптимизированного параметра кодовой книги. В этом примере также используется прогнозирующий порядок 1 в качестве требуемого порядка нового оптимизированного предиктора. dpcmopt функция создает эти оптимизированные параметры, используя пилообразный сигнал x в качестве учебных данных. Далее в примере выполняется квантование самих обучающих данных; теоретически оптимизированные параметры подходят для квантования других данных, аналогичных x. Обратите внимание, что среднеквадратичное искажение здесь намного меньше, чем искажение в предыдущем примере.
t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal initcodebook = [-1:.1:1]; % Initial guess at codebook % Optimize parameters, using initial codebook and order 1. [predictor,codebook,partition] = dpcmopt(x,1,initcodebook); % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выходные данные:
distor =
0.0063