Скалярное квантование - это процесс, который отображает все входы в заданном диапазоне на общее значение. Этот процесс сопоставляет входы в другом диапазоне значений с другим общим значением. В действительности скалярное квантование оцифровывает аналоговый сигнал. Квантование определяют два параметра: разбиение и кодовая книга.
Раздел квантования определяет несколько смежных неперекрывающихся диапазонов значений в наборе вещественных чисел. Чтобы указать раздел в среде MATLAB ®, перечислите отдельные конечные точки различных диапазонов в векторе.
Например, если раздел разделяет действительную числовую строку на четыре набора
{x: x ≤ 0}
{x: 0 < x ≤ 1}
{x: 1 < x ≤ 3}
{x: 3 < x}
затем можно представить раздел в виде трехэлементного вектора
partition = [0,1,3];
Длина вектора секционирования на единицу меньше числа интервалов секционирования.
Кодовая книга сообщает квантователю, какое общее значение назначить входам, которые попадают в каждый диапазон разделения. Представляют кодовую книгу как вектор, длина которого совпадает с количеством интервалов разбиения. Например, вектор
codebook = [-1, 0.5, 2, 3];
является одной возможной кодовой книгой для раздела [0,1,3].
quantiz функция также возвращает вектор, который сообщает, в каком интервале находится каждый вход. Например, вывод ниже говорит, что входные записи находятся в пределах интервалов, обозначенных 0, 6 и 5 соответственно. Здесь 0-й интервал состоит из вещественных чисел, меньших или равных 3; 6-й интервал состоит из действительных чисел больше 8, но меньше или равен 9; 5-й интервал состоит из действительных чисел больше 7, но меньше или равен 8.
partition = [3,4,5,6,7,8,9]; index = quantiz([2 9 8],partition)
Выходные данные:
index =
0
6
5
Если продолжить этот пример путем определения вектора кодовой книги, например,
codebook = [3,3,4,5,6,7,8,9];
затем уравнение ниже соотносит вектор index к квантованному сигналу quants.
quants = codebook(index+1);
Эта формула для quants именно то, что quantiz функция использует, если вы вместо этого фразировать пример более сжато, как ниже.
partition = [3,4,5,6,7,8,9]; codebook = [3,3,4,5,6,7,8,9]; [index,quants] = quantiz([2 9 8],partition,codebook);
Квантование искажает сигнал. Можно уменьшить искажение, выбрав соответствующие параметры раздела и кодовой книги. Однако тестирование и выбор параметров для больших наборов сигналов со схемой точного квантования может быть утомительным. Одним из способов простого получения параметров секционирования и кодовой книги является их оптимизация в соответствии с набором так называемых обучающих данных.
Примечание
Данные обучения, которые вы используете, должны быть типичными для типов сигналов, которые вы будете квантовать.
lloyds функция оптимизирует разбиение и кодовую книгу в соответствии с алгоритмом Ллойда. Код ниже оптимизирует разбиение и кодовую книгу для одного периода синусоидального сигнала, начиная с грубого начального предположения. Затем он использует эти параметры для квантования исходного сигнала, используя параметры начального приближения, а также оптимизированные параметры. Выходные данные показывают, что среднеквадратичное искажение после квантования значительно меньше для оптимизированных параметров. quantiz функция автоматически вычисляет среднеквадратичное искажение и возвращает его в качестве третьего выходного параметра.
% Start with the setup from 2nd example in "Quantizing a Signal." t = [0:.1:2*pi]; sig = sin(t); partition = [-1:.2:1]; codebook = [-1.2:.2:1]; % Now optimize, using codebook as an initial guess. [partition2,codebook2] = lloyds(sig,codebook); [index,quants,distor] = quantiz(sig,partition,codebook); [index2,quant2,distor2] = quantiz(sig,partition2,codebook2); % Compare mean square distortions from initial and optimized [distor, distor2] % parameters.
Выходные данные:
ans =
0.0148 0.0024Квантование в секции квантования сигнала не требует априорного знания о переданном сигнале. На практике можно часто делать обоснованные догадки о настоящем сигнале на основе прошлых передач сигнала. Использование таких образованных догадок для содействия квантованию сигнала известно как предсказательное квантование. Наиболее распространенным способом предсказательного квантования является дифференциальная импульсная кодовая модуляция (DPCM).
Функции dpcmenco, dpcmdeco, и dpcmopt может помочь вам реализовать предсказательный квантователь DPCM с линейным предиктором.
Чтобы определить кодер для такого квантователя, вы должны предоставить не только раздел и кодовую книгу, как описано в «Представлять разделы и представлять кодовые книги», но также и предиктор. Предиктор - это функция, которую кодер DPCM использует для получения образованного предположения на каждом шаге. Линейный предиктор имеет вид
y(k) = p(1)x(k-1) + p(2)x(k-2) + ... + p(m-1)x(k-m+1) + p(m)x(k-m)
где x - исходный сигнал, y(k) попытки предсказать значение x(k), и p является m-кортеж вещественных чисел. Вместо квантования x сам кодер DPCM квантует предиктивную ошибку x-y. Целое число m выше называется прогнозирующим порядком. Особый случай, когда m = 1 называется дельта-модуляцией.
Если предположение для k-е значение сигнала x, на основе более ранних значений xявляется
y(k) = p(1)x(k-1) + p(2)x(k-2) +...+ p(m-1)x(k-m+1) + p(m)x(k-m)
тогда соответствующий вектор предиктора для функций панели инструментов
predictor = [0, p(1), p(2), p(3),..., p(m-1), p(m)]
Примечание
Начальный ноль в предикторном векторе имеет смысл, если рассматривать вектор как полиномиальную передаточную функцию фильтра конечной импульсной характеристики (FIR).
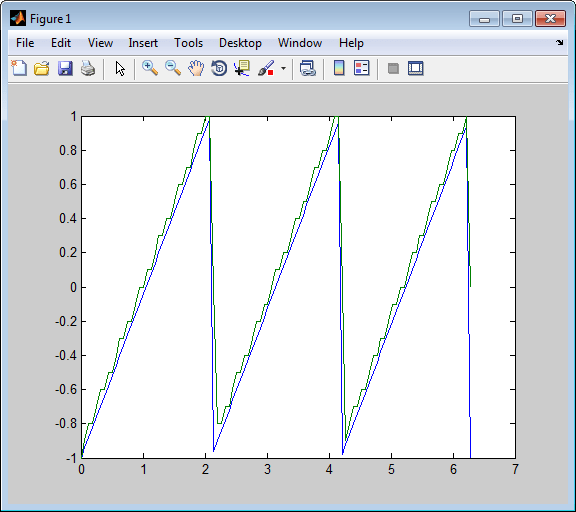
Простой частный случай DPCM квантует разность между текущим значением сигнала и его значением на предыдущем этапе. Таким образом, предсказатель просто y(k) = x (k - 1). Приведенный ниже код реализует эту схему. Он кодирует пилообразный сигнал, декодирует его и строит графики как исходного, так и декодированного сигнала. Сплошная линия является исходным сигналом, в то время как пунктирная линия является восстановленными сигналами. В примере также вычисляется среднеквадратическая ошибка между исходным и декодированным сигналами.
predictor = [0 1]; % y(k)=x(k-1) partition = [-1:.1:.9]; codebook = [-1:.1:1]; t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); plot(t,x,t,decodedx,'--') legend('Original signal','Decoded signal','Location','NorthOutside'); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выходные данные:
distor =
0.0327
В разделе «Оптимизация параметров квантования» описывается использование обучающих данных с lloyds функция, чтобы помочь найти параметры квантования, которые минимизируют искажение сигнала.
В этом разделе описаны аналогичные процедуры для использования dpcmopt функция в сочетании с двумя функциями dpcmenco и dpcmdeco, которые впервые появляются в предыдущем разделе.
Примечание
Данные обучения, используемые с dpcmopt должно быть типичным для типов сигналов, с которыми вы будете квантовать dpcmenco.
Этот пример аналогичен примеру, приведенному в последнем разделе. Однако, где был создан последний пример predictor, partition, и codebook в этом примере используется та же кодовая книга (которая теперь называется initcodebook) в качестве начального предположения для нового оптимизированного параметра кодовой книги. В этом примере также используется прогнозирующий порядок 1 в качестве требуемого порядка нового оптимизированного предиктора. dpcmopt функция создает эти оптимизированные параметры, используя пилообразный сигнал x в качестве учебных данных. Далее в примере выполняется квантование самих обучающих данных; теоретически оптимизированные параметры подходят для квантования других данных, аналогичных x. Обратите внимание, что среднеквадратичное искажение здесь намного меньше, чем искажение в предыдущем примере.
t = [0:pi/50:2*pi]; x = sawtooth(3*t); % Original signal initcodebook = [-1:.1:1]; % Initial guess at codebook % Optimize parameters, using initial codebook and order 1. [predictor,codebook,partition] = dpcmopt(x,1,initcodebook); % Quantize x using DPCM. encodedx = dpcmenco(x,codebook,partition,predictor); % Try to recover x from the modulated signal. decodedx = dpcmdeco(encodedx,codebook,predictor); distor = sum((x-decodedx).^2)/length(x) % Mean square error
Выходные данные:
distor =
0.0063
Сжатие и расширение последовательности данных с помощью Mu-закона
Сжатие и расширение последовательности данных с помощью закона
В некоторых приложениях, таких как обработка речи, обычно перед квантованием используют вычисление логарифма, называемое сжатием. Обратная работа компрессора называется расширителем. Комбинация компрессора и расширителя называется компаньоном.
Создайте последовательность данных.
data = 2:2:12
data = 1×6
2 4 6 8 10 12
Сжимайте последовательность данных с помощью mu-law компрессора. Установите значение для mu равным 255. Теперь сжатая последовательность данных находится в диапазоне от 8,1 до 12.
compressed = compand(data,255,max(data),'mu/compressor')compressed = 1×6
8.1644 9.6394 10.5084 11.1268 11.6071 12.0000
Разверните сжатую последовательность данных с помощью расширителя mu-law. Расширенная последовательность данных почти идентична исходной последовательности данных.
expanded = compand(compressed,255,max(data),'mu/expander')expanded = 1×6
2.0000 4.0000 6.0000 8.0000 10.0000 12.0000
Вычислите разницу между исходной последовательностью данных и расширенной последовательностью.
diffvalue = expanded - data
diffvalue = 1×6
10-14 ×
-0.0444 0.1776 0.0888 0.1776 0.1776 -0.3553
Создайте последовательность данных.
data = 1:5;
Сжимайте последовательность данных с помощью компрессора A-закона. Установите значение A равным 87.6. Теперь сжатая последовательность данных находится в диапазоне от 3,5 до 5.
compressed = compand(data,87.6,max(data),'A/compressor')compressed = 1×5
3.5296 4.1629 4.5333 4.7961 5.0000
Разверните сжатую последовательность данных с помощью расширителя A-закона. Расширенная последовательность данных почти идентична исходной последовательности данных.
expanded = compand(compressed,87.6,max(data),'A/expander')expanded = 1×5
1.0000 2.0000 3.0000 4.0000 5.0000
Вычислите разницу между исходной последовательностью данных и расширенной последовательностью.
diffvalue = expanded - data
diffvalue = 1×5
10-14 ×
0 0 0.1332 0.0888 0.0888
Кодирование Хаффмана предлагает способ сжатия данных. Средняя длина кода Хаффмана зависит от статистической частоты, с которой источник производит каждый символ из своего алфавита. Словарь кода Хаффмана, который связывает каждый символ данных с кодовым словом, имеет свойство, что ни одно кодовое слово в словаре не является префиксом любого другого кодового слова в словаре.
huffmandict, huffmanenco, и huffmandeco функции поддерживают кодирование и декодирование Хаффмана.
Примечание
Для длинных последовательностей из источников, имеющих искаженные распределения и малые алфавиты, арифметическое кодирование сжимается лучше, чем кодирование Хаффмана. Сведения об использовании арифметического кодирования см. в разделе Арифметическое кодирование.
Кодирование Хаффмана требует статистической информации об источнике кодируемых данных. В частности, p входной аргумент в huffmandict функция перечисляет вероятность, с которой источник создает каждый символ в своем алфавите.
Например, рассмотрим источник данных, который производит 1 с вероятностью 0,1, 2 с вероятностью 0,1 и 3 с вероятностью 0,8. Основным вычислительным шагом в кодировании данных из этого источника с использованием кода Хаффмана является создание словаря, который связывает каждый символ данных с кодовым словом. Пример здесь создает такой словарь и затем показывает вектор кодового слова, связанный с конкретным значением из источника данных.
В этом примере показано, как создать словарь кода Хаффмана с помощью huffmandict функция.
Создайте вектор символов данных и назначьте вероятность каждому.
symbols = [1 2 3]; prob = [0.1 0.1 0.8];
Создайте словарь кода Хаффмана. Наиболее вероятный символ 3 данных связан с однозначным кодовым словом, в то время как менее вероятные символы данных связаны с двухзначными кодовыми словами.
dict = huffmandict(symbols,prob)
dict=3×2 cell array
{[1]} {[1 1]}
{[2]} {[1 0]}
{[3]} {[ 0]}
Отображение второй строки словаря. Выходные данные также показывают, что кодер Хаффмана принимает символ данных. 2 заменяет последовательность 1 0.
dict{2,:}ans = 2
ans = 1×2
1 0
В примере выполняется кодирование и декодирование Хаффмана с использованием источника, алфавит которого имеет три символа. Обратите внимание, что huffmanenco и huffmandeco функции используют словарь, созданный huffmandict.
Создайте последовательность данных для кодирования.
sig = repmat([3 3 1 3 3 3 3 3 2 3],1,50);
Определите набор символов данных и вероятность, связанную с каждым элементом.
symbols = [1 2 3]; p = [0.1 0.1 0.8];
Создайте словарь кода Хаффмана.
dict = huffmandict(symbols,p);
Кодирование и декодирование данных. Убедитесь, что исходные данные, sigи декодированные данные, dhsig, идентичны.
hcode = huffmanenco(sig,dict); dhsig = huffmandeco(hcode,dict); isequal(sig,dhsig)
ans = logical
1
Арифметическое кодирование предлагает способ сжатия данных и может быть полезным для источников данных, имеющих небольшой алфавит. Длина арифметического кода вместо фиксации относительно количества кодируемых символов зависит от статистической частоты, с которой источник выдает каждый символ из своего алфавита. Для длинных последовательностей из источников, имеющих искаженные распределения и малые алфавиты, арифметическое кодирование сжимается лучше, чем кодирование Хаффмана.
arithenco и arithdeco функции поддерживают арифметическое кодирование и декодирование.
Арифметическое кодирование требует статистической информации об источнике кодируемых данных. В частности, counts входной аргумент в arithenco и arithdeco функции перечисляют частоту, с которой источник выдает каждый символ в своем алфавите. Частоты можно определить, изучив набор тестовых данных из источника. Набор тестовых данных может иметь любой выбранный размер, если каждый символ в алфавите имеет ненулевую частоту.
Например, перед кодированием данных из источника, который производит 10 x, 10 y и 80 z в типичном наборе тестовых данных из 100 символов, определите
counts = [10 10 80];
Альтернативно, если больший набор тестовых данных из источника содержит 22 x, 23 y и 185 z, то определите
counts = [22 23 185];
Кодируют и декодируют последовательность из источника, имеющего три символа.
Создайте вектор последовательности, содержащий символы из набора {1,2,3}.
seq = [3 3 1 3 3 3 3 3 2 3];
Установите counts вектор для определения кодера, который производит 10 единиц, 20 двойок и 70 троек из типичного 100-символьного набора тестовых данных.
counts = [10 20 70];
Примените функции арифметического кодера и декодера.
code = arithenco(seq,counts); dseq = arithdeco(code,counts,length(seq));
Убедитесь, что выходной сигнал декодера соответствует исходной входной последовательности.
isequal(seq,dseq)
ans = logical
1
Код ниже показывает, как quantiz функции использует partition и codebook для отображения реального вектора, samp, к новому вектору, quantized, записи которых имеют значения -1, 0,5, 2 или 3.
partition = [0,1,3]; codebook = [-1, 0.5, 2, 3]; samp = [-2.4, -1, -.2, 0, .2, 1, 1.2, 1.9, 2, 2.9, 3, 3.5, 5]; [index,quantized] = quantiz(samp,partition,codebook); quantized
Выходные данные приведены ниже.
quantized =
Columns 1 through 6
-1.0000 -1.0000 -1.0000 -1.0000 0.5000 0.5000
Columns 7 through 12
2.0000 2.0000 2.0000 2.0000 2.0000 3.0000
Column 13
3.0000
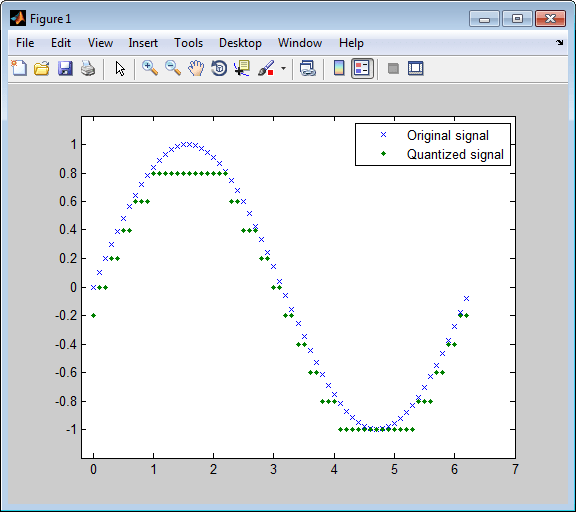
Этот пример иллюстрирует характер скалярного квантования более ясно. После квантования дискретизированного синусоидального сигнала он строит график исходного и квантованного сигналов. Сюжет контрастирует xОни составляют синусоидальную кривую с точками, составляющими квантованный сигнал. Вертикальная координата каждой точки - это значение вектора codebook.
t = [0:.1:2*pi]; % Times at which to sample the sine function sig = sin(t); % Original signal, a sine wave partition = [-1:.2:1]; % Length 11, to represent 12 intervals codebook = [-1.2:.2:1]; % Length 12, one entry for each interval [index,quants] = quantiz(sig,partition,codebook); % Quantize. plot(t,sig,'x',t,quants,'.') legend('Original signal','Quantized signal'); axis([-.2 7 -1.2 1.2])