Инвертировать модели
inv
inv(sys,'min')
inv инвертирует отношение «вход-выход»
ы) u
для получения модели с матрицей переноса s) − 1.
ы) y
Эта операция определяется только для квадратных систем (одинаковое количество входов и выходов) с обратимой матрицей D. inv обрабатывает как непрерывные, так и дискретно-временные системы.
inv(sys,'min') обратные своды sys устранить дополнительные состояния и получить модель с таким количеством состояний, как sys или A соответственно. Для ss, genss и uss по умолчанию обратная модель возвращается в неявном виде. Эта опция игнорируется для разреженных моделей, поскольку обычно уничтожает разреженность. Использовать isproper или ss(sys,'explicit') для извлечения явной модели при необходимости.
Рассмотреть
101]
В подсказке MATLAB ® введите
H = [1 tf(1,[1 1]);0 1] Hi = inv(H)
чтобы инвертировать его. Эти команды дают следующий результат.
Transfer function from input 1 to output...
#1: 1
#2: 0
Transfer function from input 2 to output...
-1
#1: -----
s + 1
#2: 1
Вы можете проверить, что
H * Hi
- функция передачи идентичности (статический коэффициент усиления I).
Не использовать inv для моделирования соединений обратной связи, таких как
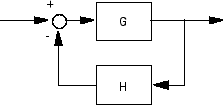
В то время как представляется разумным оценить соответствующую передаточную функцию с замкнутым контуром − 1G как
inv(1+g*h) * g
это, как правило, приводит к неминумальным моделям с замкнутым контуром. Например,
g = zpk([],1,1) h = tf([2 1],[1 0]) cloop = inv(1+g*h) * g
дает модель третьего порядка с замкнутым контуром с нестабильной отменой полюса-нуля при s = 1.
cloop
Zero/pole/gain:
s (s-1)
-------------------
(s-1) (s^2 + s + 1)
Использовать feedback чтобы избежать таких подводных камней.
cloop = feedback(g,h)
Zero/pole/gain:
s
-------------
(s^2 + s + 1)